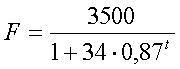HAVO WB1,  2000 - I
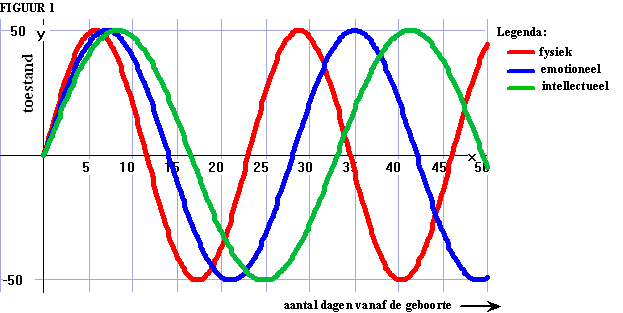
Bioritme

Op een pagina op Internet staat te lezen dat ons leven beheerst wordt door een drietal toestanden, namelijk door onze fysieke, onze emotionele en onze intellectuele toestand. Op de ene dag voel je je fysiek (lichamelijk) beter dan op een andere dag. Deze 'fysieke' toestand kunnen we weergeven op een schaal van -50 (fysiek op dieptepunt) tot +50 (fysiek opperbest). Deze fysieke toestand varieert in de tijd volgens een sinusoïde.
Ook de emotionele toestand en de intellectuele toestand variëren op een schaal van -50 tot +50 volgens een sinusoïde. Zie figuur 1.
Bij de geboorte van een mens zou elke cyclus zich in dezelfde begintoestand bevinden, zoals is weergegeven in figuur 1.
Tezamen bepalen de drie cycli het zogenaamde bioritme van de mens. Sommigen beweren dat het bioritme volledig vastlegt tot welke prestaties een mens op een bepaald moment in staat is. Zo zou je bijvoorbeeld kunnen uitrekenen op welke dag je het best kunt solliciteren. Voor de fysieke cyclus is de periode 23 dagen, voor de emotionele cyclus 28 dagen en voor de intellectuele cyclus is de periode 33 dagen.
Het bioritme in figuur 1 betreft een pasgeboren baby. E is de emotionele toestand van de baby, t dagen na de geboorte. Hierbij hoort de formule van de vorm  E = a sin bt
3p 1. Geef de waarden van a en b.

 
Zodra de emotionele toestand beneden -25 komt zou het moeilijker worden om de emoties onder controle te houden.
5p 2. Hoeveel procent van een periode heeft de emotionele toestand een waarde die kleiner is dan -25? Licht je antwoord toe.

 
F is de fysieke toestand van de baby.
5p 3. Onderzoek of F op de eerste verjaardag een dalend of een stijgend verloop heeft.

 
Annelies is op 1 januari 1983 geboren. Op 1 januari 2001 wordt ze dus 18 jaar. Vanaf die dag mag ze rijexamen doen. Ze wil dat doen op een dag waarop zowel haar fysieke als haar intellectuele toestand positief is.
(de jaren 1984, 1988, 1996 en 2000 hebben een dag extra, dus 366 dagen)
7p 4. Onderzoek welke de eerste drie dagen van januari 2001 zijn die voor het rijexamen in aanmerking komen.

Bestrijdingsmiddelen
Bij de teelt van winterpeen worden in Nederland bestrijdingsmiddelen toegepast.
Om zicht te krijgen op de belasting van het milieu worden de telers van winterpeen ingedeeld in twee groepen

I:  de groep die chemische bestrijdingsmiddelen gebruikt.
II:  de groep die geen chemische bestrijdingsmiddelen gebruikt: tot deze groep behoren de telers die milieuvriendelijke bestrijdingsmiddelen gebruiken.

Neem aan dat in 1995 voor groep I de toegepaste hoeveelheid chemisch bestrijdingsmiddel per hectare normaal verdeeld is met een gemiddelde van 5,2 kg en een standaardafwijking van 0,7 kg.
4p 5. Bereken voor 1995 op hoeveel procent van de grondoppervlakte van de telers in groep I meer dan 5,5 kg bestrijdingsmiddel per hectare werd gebruikt.

Een actiegroep vindt dat in 1995 op 25% van de grondoppervlakte van de telers in groep I een te grote dosis chemische bestrijdingsmiddelen is toegepast.
4p 6. Bereken de maximale dosis per hectare die de actiegroep nog acceptabel vindt.

Uit de gegevens van het Centraal Bureau voor de Statistiek over 1995 blijkt dat voor de teelt van winterpeen door de groepen I en II samen gemiddeld 4,6 kg bestrijdingsmiddel per hectare werd gebruikt. In totaal werd er voor deze groente in ons land 21 ton gebruikt (1 ton = 1000 kg)
4p 7. Bereken op hoeveel hectare bij de teelt van winterpeen geen chemische bestrijdingsmiddelen werden toegepast.

De actiegroep neemt aan dat in het jaar 2000 het gebruik van chemische bestrijdingsmiddelen als volgt zal zijn:
  • op 15% van de totale grondoppervlakte voor winterpeen teelt men zonder chemische bestrijdingsmiddelen.
  • op de overige grond is de toegepaste hoeveelheid chemische bestrijdingsmiddelen normaal verdeeld met een gemiddelde van 4,2 kg en een standaardafwijking van 0,6 kg.
Bij deze twee aannames maakt de actiegroep voor het jaar 2000 een tabel van het verwachte gebruik van bestrijdingsmiddelen bij de teelt van winterpeen. Zie tabel 1 met klassenindeling.
Twee percentages zijn al ingevuld.
TABEL 1
hoeveelheid chemisch
bestrijdingmiddel (kg/ha)		 van 0 tot
en met 3		 van 3 tot
en met 4		 van 4 tot
en met 5		 meer dan
5
percentage van de totale
grondoppervlakte voor winterpeen		     46 8
7p 8. Bereken de twee percentages die nog niet in de tabel staan. Licht je werkwijze toe.

Fruitvliegjes
Bij een experiment met fruitvliegjes in een afgesloten ruimte heeft men vastgesteld dat het aantal fruitvliegjes per m3 bij benadering beschreven kan worden met de volgende formule:
Hierin is t de tijd in dagen vanaf de start van het experiment, en F het aantal fruitvliegjes per m3 op tijdstip t.
3p 9. Na hoeveel dagen vanaf het begin van het experiment zijn er voor het eerst meer dan 2500 fruitvliegjes per m3? Licht je antwoord toe.

Het aantal fruitvliegjes per m3 neemt toe tot een bepaalde grenswaarde.
3p 10. Hoe groot is deze grenswaarde? Licht je antwoord toe.

Het aantal fruitvliegjes neemt eerst steeds sneller en later steeds langzamer toe.
5p 11. Op hoeveel dagen neemt het aantal fruitvliegjes per dag met meer dan 75 per m3 toe? 
Licht je antwoord toe.

Als bij het experiment de tijd t niet gemeten wordt in dagen maar in uren, geldt voor het aantal fruitvliegjes per m3 een andere formule.
De tijd in uren vanaf het begin van het experiment is T.
3p 12. Stel een formule op voor het aantal fruitvliegjes F op tijdstip T.

Bloemenvaas
Een wiskundige heeft met behulp van een functie een mal voor een vaas geproduceerd.
Zie figuur 2.
In figuur 3 is in een assenstelsel een verticale dwarsdoorsnede van de binnenkant van de vaas getekend. Hierbij is de dwarsdoorsnede over een hoek van 90° gedraaid ten opzichte van figuur 2. De binnenkant van de vaas is symmetrisch ten opzichte van de x-as.
De lijnstukken AB en CD zijn middellijnen van de cirkelvormige onder- en bovenkant van de vaas.
Het gedeelte AC van de doorsnede in figuur 3 is de grafiek van een functie f met functievoorschrift:
f(x) = 0,0028x3 - 0,12x2 + 1,3x + 5
met x en f(x) in centimeter
3p 13. Bereken de diameter CD van de bovenkant van de vaas.
     
5p 14. Bereken de diameter van de dikste bos bloemen die nog net door het smalle bovendeel van de vaas kan. Geef je antwoord in één decimaal nauwkeurig.

De dikte van de vaas, steeds horizontaal gemeten, is 0,5 cm. In figuur 3 zijn twee binnenzijden van de vaas getekend.
3p 15. Geef formules van de twee bijbehorende buitenzijden.

In de vaas van figuur 2 wordt water gegoten tot de waterspiegel 20 cm hoog staat. Een bloem met een rechte stengel wordt zo in de vaas geplaatst dat de stengel de binnenrand raakt in punt C. De dikte van de stengel mag hier worden verwaarloosd.
8p 16. Onderzoek of de voet van de stengel dan onder water staat.
Euro-mix
Op 1 januari 2002 wordt in 11 landen van de Europese gemeenschap het nieuwe muntstelsel van de euro ingevoerd, De eurolanden beschikken dan over het zelfde betaalmiddel. Wel geeft ieder land zijn euromunten een eigen nationaal kenmerk door op één zijde van de munt een karakteristieke afbeelding aan te brengen (bijvoorbeeld koningin Beatrix in Nederland,  Marianne in Frankrijk, ...). In elk euroland mogen echter alle munten van het eurostelsel gebruikt worden, ongeacht de afbeelding.
Zo zal er vermenging optreden van de eigen euromunten van een land met 'vreemde' (= buitenlandse) euromunten.

Neem aan dat in een bepaald gebied op een zeker moment 10% van de aanwezige euromunten vreemd is. Iemand wisselt in dit gebied een biljet van 10 euro tegen tien munten van 1 euro.
3p 17. Bereken de kans dat precies twee van deze munten vreemd zijn. Geef je antwoord in twee decimalen nauwkeurig.

Een winkelier uit ditzelfde gebied zegt er voor meer dan 95% van zeker te zijn dat van honderd willekeurig gekozen munten in zijn opbrengst het aantal vreemde munten tussen 5 en 15 ligt.
6p 18. Onderzoek of de winkelier gelijk heeft.

Doordat de euromunten van alle nationaliteiten door elkaar circuleren kan een vreemde munt via veel verschillende transacties in ons land terechtkomen. De volgende voorbeelden laten zien hoe een Spaanse euromunt na vier transacties binnen de 11 eurolanden van Spanje in Nederland terecht kan komen.
van via via via naar
voorbeeld 1: Spanje Spanje Frankrijk Duitsland Nederland
voorbeeld 2: Spanje Italië Nederland Denemarken Nederland
4p 19. Op hoeveel manieren kan een Spaanse euro na 15 transacties binnen de eurolanden van Spanje in Nederland terechtkomen? Licht je antwoord toe.

Burgers Bush is een dierentuin in Arnhem. Door de gunstige ligging bezoeken veel Duitsers deze dierentuin. Neem aan dat op een zeker moment de vermenging van euro's zover is dat voor het muntbezit van de bezoekers van Burgers Bush de onderstaande tabel van toepassing is.
  Nederlandse euromunten Duitse euromunten Overige euromunten
Nederlander 70% 20% 10%
Duitser 10% 85% 5%
Bij de dierentuin is een groot parkeerterrein. In het weekend is gemiddeld 40% van de auto's op het terrein van een Duitse eigenaar; 60% van de auto's is van Nederlandse eigenaar. Bij het verlaten van het parkeerterrein moet er een muntstuk van 1 euro in een apparaat gedaan worden om de slagboom te openen.
Iemand beweert dat in de parkeeropbrengst van het weekend het percentage Duitse euro's gemiddeld groter is dan het percentage Nederlandse euro's.
5p 20. Onderzoek of deze bewering waar is.

OPLOSSINGEN
Het officiële (maar soms beknoptere) correctievoorschrift kun je HIER vinden. Vooral handig voor de onderverdeling van de punten.
1. a is de amplitude en die is a = 50.
de periode is 28 dagen dus  b = 2π/28 = 0,224
2. 1e opl. Voer in de rekenmachine in  Y1 = 50 • sin(2pt/28) en Y2 = -25
INTERSECT  levert  t ≈ 16,3  en  t ≈ 25,7
Daartussen liggen 9,4 dagen per periode van 28. Dat is ongeveer 33%.
2e opl. Algebraïsch:
50 • sin(2pt/28) = -25  ⇒ sin(2pt/28) = -0,5 ⇒ 2pt/28 = 7p/6  of  2pt/28 = 11p/6
⇒ t = 196/12  of  t = 308/12  en verder gaat het zoals in de 1e oplossing.
3. F heeft amplitude 50 en periode 23 dagen.
Dat geeft de formule  F(t) = 50 • sin(2πt/23)
De eerste verjaardag duurt van  t = 365 tot t = 366  of van t = 366 tot t = 367 (in een schrikkeljaar)
Een plot van F(t) tussen bijvoorbeeld t = 360 en t = 370 laat zien dat F daar stijgt.
4. I heeft amplitude 50 en periode 33 dagen.
Dat geeft de formule  I(t) = 50 • sin(2pt/33)
Het aantal verstreken dagen tot 1 januari 2001 is  18 • 365 + 5 = 6575
Een plot van F en I tussen t = 6575 en t = 6585 laat zien dat t = 6578, 6579 en 6580 de gezochte dagen zijn.
Dat zijn dus  4, 5 en 6 januari.
(Als Annelies 's avonds is geboren kun je uitkomen op  5, 6 en 7 januari)
5. NORMALCDF(5.5 , 1E99 , 5.2 , 0.7) = 0,334117... Dus ongeveer 33%.
6. Dan moet gelden NORMALCDF(X , 1E99 , 5.2 , 0.7) = 0,25
Invoeren in de GR in INTERSECT gebruiken levert X = 5,6721.... 
dus het maximum is ongeveer 5,7 kg per hectare.
7. Noem de aantallen hectaren bij groep I en groep II respectievelijk h1 en h2.
Bij h2 worden geen bestrijdingsmiddelen gebruikt, dus 5,2 • h1 = 21000  ofwel  h1 = 4038 ha
Gemiddeld over h1 en h2 samen geldt  4,6 = 21000/(h1 + h2)
Vul daarin in dat h1 = 4038 en je vindt  h2 = 527 ha.
8. Op grond waar bestrijdingsmiddelen worden gebruikt (en dat is 85% van het totaal) is de hoeveelheid gebruikte bestrijdingsmiddelen normaal verdeeld met gemiddelde 4,2 en standaardafwijking 0,5.
Minder dan 3 is dan NORMALCDF(-1E99 , 3 , 4.2 , 0.5) = 0,0228  dus  2,28%.
Dus op 2,28% van de 85% wordt minder dan 3 kg/ha gebruikt.
Dat is  0,0228 • 0,85 = 0,01938 = 1,938% van de totale grond.
Op 15% van de grond wordt helemaal geen bestrijdingsmiddelen gebruikt.
In het hokje van 0 tm 3 komt dus te staan  1,938 + 15 ≈ 17%
Dan blijft voor het hokje 3 tm 4 nog over  100 - 17 - 46 - 8 = 29%
9. 1e opl. Voer de F-formule in bij Y1 in de Grafische rekenmachine.
Gebruik INTERSECT (of TABLE) om te vinden dat er na 31,9 dagen voor het eerst meer dan 2500 vliegjes zijn.
2e opl. Algebraïsch:
F = 2500  ⇒ 3500 = 2500 • (1 + 34 • 0,87t) ⇒ 3500 = 2500 + 85000 • 0,87t
⇒ 1000 = 85000 • 0,87t ⇒  0,87t = 0,01176...  ⇒  t = log(0,01176...)/log(0,87) = 31,9 dagen.
10. Door voor t een heel groot getal in te vullen (of in de tabel te kijken bij grote t) is te zien dat de grenswaarde gelijk is aan 3500.
Het is ook aan de formule te zien:  34 • 0,87t  zal voor grote t nul worden, dus blijft 3500 over.
11. Een tabel op de rekenmachine brengt uitkomst.
Zet bij  Y1 de F-formule, en bij Y2 de formule  Y2 = Y1(X) - Y1(X - 1)  dan staat bij Y2 de toename vanaf de vorige dag. (Y1 vind je onder de knop VARS)
In de tabel zie je dat van dag 16 tot en met dag 36 de toename meer dan 75 is, dus dat is 21 dagen.
12. Vervang t door  T/24. Immers als je dan voor T = 24 invult (1 dag) komt dat inderdaad overeen met  t = 1
13. BC ligt aan de binnenkant van de vaas.
f(30) = 11,6. Dus  CD = 2 • 11,6 = 23,3 cm.
14. 1e opl. Voer de formule in in de GR en bereken met CALC - Minimum het minimum van de grafiek want daar zal de vaas het smalst zijn. Dat geeft  x = 21,3  met  y= 5,31.
De dikste bos bloemen heeft dus een diameter van  2 • 5,31 = 10,6 cm.
2e opl. Voor het minimum van f geldt dat de afgeleide nul is:
f ' (x) = 0,0084x2 - 0,24x + 1,3
0,0084x2 - 0,24x + 1,3  = 0  geeft met de ABC-formule  x = 7,3 (maar dat is het maximum) of  x = 21,3.
De laatste waarde geeft het minimum. y is daar 5,31.
De dikste bos bloemen heeft dus een diameter van  2 • 5,31 = 10,6 cm.
15. De buitenzijde bij BC ligt 0,5 cm hoger dan de binnenzijde. Dat krijgen we door de grafiek van  f  0,5 cm omhoog te schuiven en dat kan door de formule van f  "+0,5" te doen.
f(x) = 0,0028x3 - 0,12x2 - 1,3x + 5,5

De buitenzijde onder AD is het spiegelbeeld van de andere buitenzijde.
Spiegelen in de x-as krijgen we door de hele formule van een minteken te voorzien.
f(x) = -0,0028x3 + 0,12x2 + 1,3x - 5,5
16. De steel van de roos is de raaklijn aan de grafiek van f in punt C (30 , 11.6)
De raaklijn heeft de formule  y = ax + b
f '(x) = 0,0084x2 - 0,24x + 1,3  dus  f '(30) = 1,66 en dat is de a van de raaklijn.
De raaklijn wordt daarmee  y = 1,66 • x + b
Vul nu het punt C in:  11,6 = 1,66 • 30 + b  dat geeft  b = -38,2
De raaklijn wordt daarmee   y = 1,66 • x - 38,2
(deze formule had je overigens ook direct kunnen vinden: voer de formule voor f in bij Y1 in de GR en gebruik de optie DRAW - Tangent)

Stel nu deze raaklijnformule gelijk aan de formule voor de onderkant van de vaas:
1,66 • x - 38,2 = -0,0028x3 + 0,12x2 + 1,3x - 5
Invoeren in Y2 en Y2 en INTERSECT gebruiken levert snijpunt  x = 19,7
Conclusie: de stengel staat net in het water.
17. 1e opl. Een teruggegeven munt kan vreemd of niet-vreemd zijn. Dus het aantal vreemde munten is binomiaal verdeeld met n = 10 en p = 0,1.
BINOMPFD(10, 0.1 , 2) = 0,19
2e opl. Een teruggegeven munt kan vreemd (V: kans 0,1) of niet-vreemd (N: kans 0,9) zijn.
Een mogelijkheid voor 2 vreemde is bijv.  VVNNNNNNNN
De kans op deze serie is  0,12 • 0,98
Maar er zijn  10 nCr 2 = 45 zulke mogelijke series.
De totale kans wordt daarmee 45 • 0,12 • 0,98 = 0,19
18. Het aantal vreemde munten is binomiaal verdeeld met n = 100 en p = 0,1.
P(6 ≤ X ≤ 14) = P(X ≤ 14) - P(X ≤ 5) = BINOMCDF(100 , 0.1 , 14)  -  BINOMCFD(100 , 0.1 , 5)
= 0,92742... - 0,05757... = 0,86985... dus ongeveer 87% dus de winkelier heeft ongelijk.
19. Voor de eerste 14 transacties zijn er telkens 11 mogelijkheden (ook Nederland mag voorkomen) en voor de laatste transactie is er maar één mogelijkheid: alleen Nederland.
Totaal geeft dat  1114 • 1 = 3,8 • 1014 = 380.000.000.000.000 (380 biljoen)
20. Nederlandse euromunten:
    van Nederlander afkomstig:  0,6 • 0,7 = 0,42
    van Duitser afkomstig:           0,4 • 0,1 = 0,04
In totaal is dat 0,46 is 46%

Duitse euromunten:
    van Nederlander afkomstig:  0,6 • 0,2 = 0,12
    van Duitser afkomstig:          0,4 • 0,85 = 0,34
In totaal is dat  0,46 is 46%

De percentages Nederlandse en Duitse euro's zijn precies gelijk dus de bewering in ONJUIST.