| Uitverkoop. | |||
| Een schoenenzaak geeft korting op de wintercollectie. Er zijn twee kortingsacties (I en II) die met behulp van posters in de winkel onder de aandacht worden gebracht. Zie onderstaande figuur. | |||
|
|
|||
| Twee vriendinnen, Famke en Milla, gaan schoenen kopen. Famke koopt twee paar schoenen: een paar van 100 euro en een paar van 80 euro. Ze wil gebruikmaken van kortingsactie II. | |||
| 3p. | 1. | Bereken hoeveel procent korting Famke krijgt op haar totale aankoop. Geef je antwoord in hele procenten. | |
| Milla koopt ook twee paar schoenen: een paar van 100 euro en een paar van 40 euro. | |||
| 3p. | 2. | Onderzoek bij welke van de twee kortingsacties Milla de meeste korting krijgt. | |
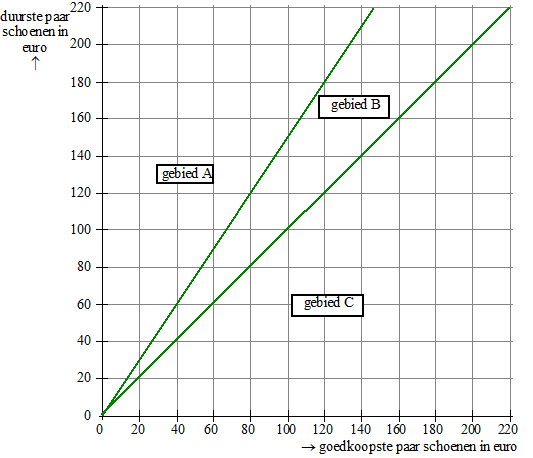
| We bekijken het kopen van twee paar schoenen uit de wintercollectie met korting. In de volgende figuur staat langs de verticale as de prijs van het duurste paar en langs de horizontale as de prijs van het goedkoopste paar schoenen. | |||
|
|
|||
| In de figuur zijn twee lijnen getekend waardoor er drie gebieden A, B en C zijn. Eén van deze drie gebieden geeft combinaties van prijzen van het duurste en goedkoopste paar schoenen weer, waarbij kortingsactie II voordeliger is dan kortingsactie I. | |||
| 3p. | 3. | Welk gebied is dat? Licht je antwoord toe. | |
| Ondanks de kortingsacties is de wintercollectie na enkele weken nog steeds niet helemaal verkocht. De schoenenzaak gaat daarom over tot een nieuwe kortingsactie waarin nog meer korting wordt gegeven: de ‘final wintersale’. Zie de onderstaande figuur. Deze final wintersale bestaat ook weer uit twee kortingsacties (I en II), waarover het in de rest van deze opgave gaat. | |||
|
|
|||
| De meeste klanten
denken nu dat bij de aankoop van twee paar schoenen kortingsactie II
altijd meer korting oplevert dan kortingsactie I. Dit is echter niet
juist. Stel dat het goedkoopste paar G euro kost en het duurste
paar f keer zo duur is. Dan kunnen we de (totale) korting (in
euro) berekenen voor beide kortingsacties met de onderstaande formules:
Korting bij kortingsactie I: KI = 0,3 · G + 0,3 · f · G Korting bij kortingsactie II: KII = 0,75 · G Als bijvoorbeeld het goedkoopste paar schoenen 30 euro kost en het duurste paar drie keer zo duur is, dan is de totale korting bij kortingsactie I gelijk aan 0,3 · 30 + 0,3 · 3 · 30 = 36 euro. Stel dat het goedkoopste paar 75 euro kost. |
|||
| 3p. | 4. | Bereken hoeveel keer zo duur (als het goedkoopste paar) het duurste paar maximaal mag zijn, zodat kortingsactie II minstens evenveel korting oplevert als kortingsactie I. | |
| Met behulp van de
formule voor I kunnen we een formule opstellen voor het bedrag B
(in euro) dat de klant uiteindelijk moet betalen bij kortingsactie I:
B = 0,7 · G + 0,7 · f · G |
|||
| 2p. | 5. | Laat zonder getallenvoorbeelden zien hoe deze formule opgesteld kan worden. | |
| Vlindertellingen. | |||
| Voor de Vlinderstichting
tellen vrijwilligers in heel Nederland vlinders vanaf maart tot en
met september. Deze vlindertellingen vinden al meerdere jaren
plaats. De vrijwilligers tellen dan alle vlinders die ze zien, één
keer per week, op een vaste dag en op vaste routes van ongeveer een
kilometer. In 1989 telden vrijwilligers vlinders op 69 vaste routes. Sindsdien steeg het aantal vaste routes waarop vrijwilligers vlinders telden vrijwel lineair tot 394 routes in 2014. |
|||
| 3p. | 6. | Bereken met behulp van lineair interpoleren het aantal vaste routes in 2002 waarop vrijwilligers vlinders telden. | |
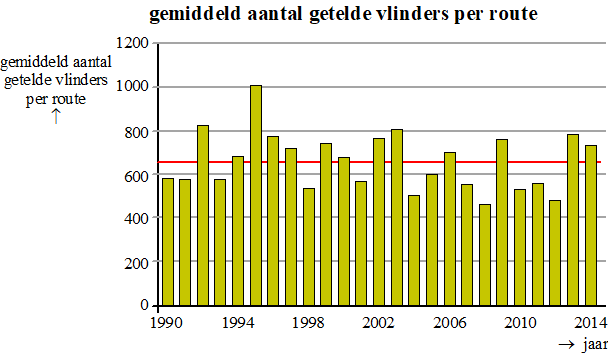
| In onderstaande figuur zie je per jaar het gemiddeld aantal getelde vlinders per route weergegeven voor de periode 1990-2014. Zo zie je dat in 1990 gemiddeld bijna 600 vlinders per route geteld zijn. Het gemiddelde over de hele periode 1990-2014 is met de horizontale lijn aangegeven. In 1990 is het gemiddeld aantal getelde vlinders per route lager dan het gemiddelde over de periode 1990-2014. | |||
|
|
|||
| 3p. | 7. | Onderzoek voor de periode 1990-2014 of de mediaan van het gemiddeld aantal getelde vlinders per route groter of kleiner is dan het gemiddelde over die hele periode. | |
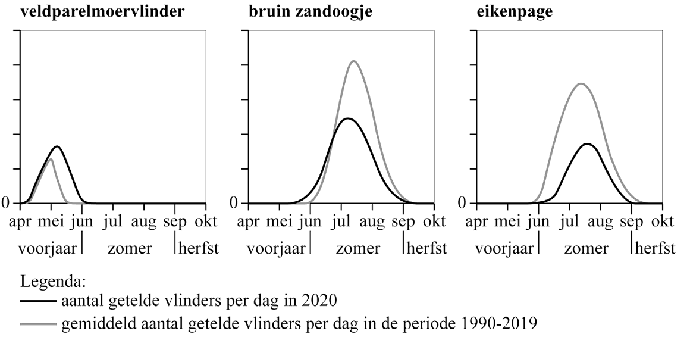
| Tijdens de vlindertelling zijn in een bepaald gebied drie vlindersoorten geteld. In de volgende figuur zie je van deze drie vlindersoorten de getelde aantallen in 2020 (zwarte lijn) en de gemiddelde aantallen in de periode 1990-2019 (grijze lijn). De schaalverdeling op de assen is bij elk van de drie grafieken hetzelfde. | |||
|
|
|||
| Bij deze figuur zijn de volgende stellingen geformuleerd: | |||
| I | Deze vlindersoort wordt in 2020 tijdens een kortere periode waargenomen dan gemiddeld in de periode 1990-2019. | ||
| II | Deze vlindersoort is de meest waargenomen vlinder in 2020. | ||
| III | In het voorjaar van 2020 wordt deze vlindersoort vaker waargenomen dan gemiddeld in de periode 1990-2019. | ||
| Elke stelling is van toepassing op minstens een van de drie vlindersoorten in de figuur. | |||
| 3p. | 8. | Geef bij elke stelling een vlindersoort waarop die stelling van toepassing is. Licht je antwoord toe. | |
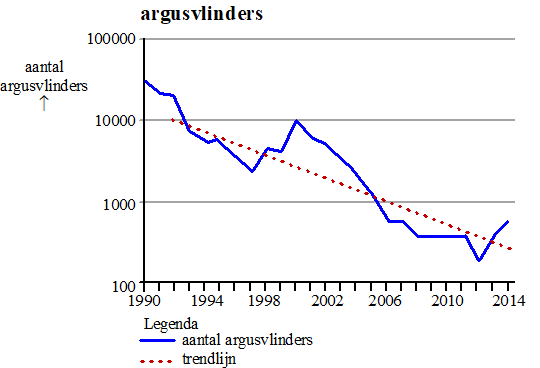
| In onderstaande figuur zie je hoe het aantal getelde argusvlinders in een bepaald gebied zich in de loop van de tijd ontwikkeld heeft. De aantallen zijn op een logaritmische schaal weergegeven. | |||
|
|
|||
| De rechte lijn in deze figuur is de trendlijn. Volgens deze trendlijn neemt het aantal argusvlinders af. | |||
| 4p. | 9. | Bereken met hoeveel procent per jaar het aantal argusvlinders volgens de trendlijn afneemt. Geef je antwoord in één decimaal. | |
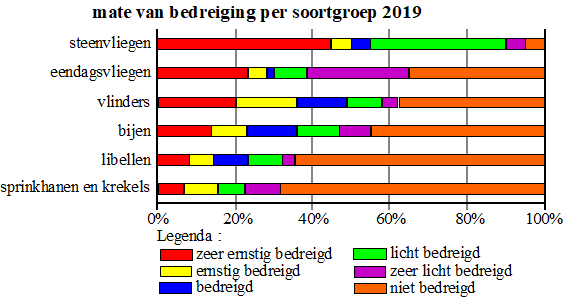
| Bij de Vlinderstichting worden behalve de gegevens van vlinders ook de gegevens van andere insectensoorten verwerkt, zoals van libellen. In onderstaande figuur zie je hoe het met de verschillende soortgroepen gaat in 2019. | |||
|
|
|||
| 4p. | 10. | Onderzoek met behulp van het formuleblad of er een groot, middelmatig of gering verschil is tussen vlinders en libellen in de mate van bedreiging. | |
| Extreme armoede. | |||||||||||||||||||||||||||||||||||||||||||||||
| De
Wereldbank stelt dat iemand in extreme armoede leeft wanneer hij
of zij moet leven van minder dan 1,90 Amerikaanse dollar (US$)
per dag (uitgaande van basisjaar 2011). Dit bedrag wordt de
internationale armoedegrens genoemd. In de tabel staat, voor de periode 1990-2015, uitgaand van de internationale armoedegrens, hoeveel mensen wereldwijd in extreme armoede leefden en welk percentage van de wereldbevolking dat was. |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||
| In 2015 had de Wereldbank de ambitie om het percentage van de wereldbevolking dat in extreme armoede leeft, uiterlijk in het jaar 2030 onder de 3,0 te krijgen. De Wereldbank rapporteert dat in de periode 1990-2015 dit percentage bij benadering jaarlijks met 1 afnam. Neem aan dat deze constante daling zich na 2015 op dezelfde wijze voortzet. | |||||||||||||||||||||||||||||||||||||||||||||||
| 3p. | 11. | Onderzoek of de ambitie van de Wereldbank volgens deze benadering gehaald zal worden. | |||||||||||||||||||||||||||||||||||||||||||||
| We nemen
aan dat de wereldbevolking in de periode van 1990-2015
exponentieel groeide en we maken gebruik van de gegevens van
1990 en 2015. Hieruit volgt de volgende formule, die een goede
benadering voor de omvang van de wereldbevolking geeft: B = 5,28 · 1,013t Hierin is B de wereldbevolking in miljarden en t het aantal jaren na 1990. |
|||||||||||||||||||||||||||||||||||||||||||||||
| 5p. | 12. | Laat zien hoe deze formule uit bovenstaande aanname en de genoemde gegevens volgt. | |||||||||||||||||||||||||||||||||||||||||||||
| De
internationale armoedegrens is voor iedereen in de wereld
gelijk, dus onafhankelijk van het land waarin iemand leeft.
Onderzoekers bij de Wereldbank hebben voorgesteld om bij studies
naar extreme armoede ook te kijken naar een nationale
armoedegrens N (in US$ per persoon per dag) . Deze grens
verschilt per land en ligt hoger naarmate een land welvarender
is. Hoe welvarend een land is, wordt uitgedrukt in de
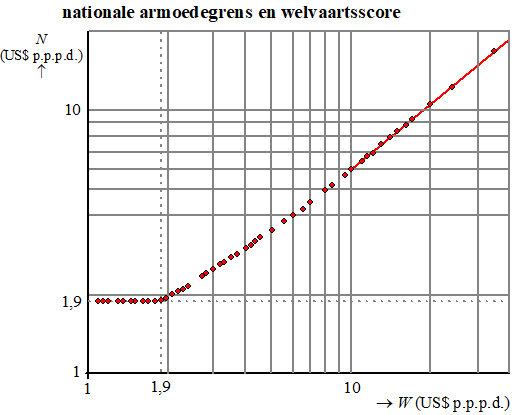
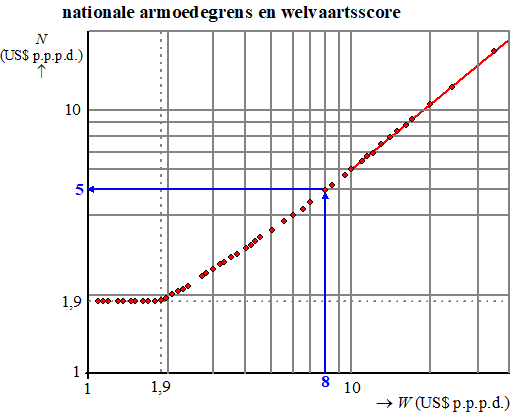
welvaartsscore W (in US$ per persoon per dag). In de figuur is van diverse landen het verband weergegeven tussen de nationale armoedegrens N en de welvaartsscore W. Beide assen in de figuur hebben een logaritmische schaalverdeling. Er is een lijn getekend die past bij de losse punten in het rechterdeel van de figuur. |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
| Een land heeft een welvaartsscore van 8. | |||||||||||||||||||||||||||||||||||||||||||||||
| 2p. | 13. | Bepaal met behulp van de figuur de nationale armoedegrens in dit land. | |||||||||||||||||||||||||||||||||||||||||||||
| In de
figuur is te zien dat de nationale armoedegrens nooit onder de
internationale armoedegrens van 1,9 komt. In de figuur is een
lijn getekend door de punten met W ł
10 . Bij deze lijn past de formule: N = 0,88 · W0,83 (formule 1) De onderzoekers gebruikten echter in hun rapport een andere formule: N = 1,00 + 0,5 · W (formule 2) In beide formules is N de nationale armoedegrens van een land en W de welvaartsscore van dat land, beide in US$ per persoon per dag. Beide formules zijn geldig voor W ł 10 Formule 2 geeft steeds een grotere uitkomst voor N dan formule 1. De onderzoekers konden formule 2 toch gebruiken, omdat de uitkomsten van de twee formules niet veel van elkaar verschillen voor bepaalde welvaartsscores W. |
|||||||||||||||||||||||||||||||||||||||||||||||
| 4p. | 14. | Bereken tot en met welke welvaartsscore W het verschil tussen de uitkomsten van beide formules voor N kleiner is dan 1. Geef je antwoord in één decimaal. | |||||||||||||||||||||||||||||||||||||||||||||
| Het gebruik
van de nationale armoedegrens in plaats van de internationale
armoedegrens leidt tot een andere kijk op de omvang van het
probleem van extreme armoede in de wereld. Voor het aantal
mensen dat in extreme armoede leeft, gelden bij benadering de
volgende formules: Ai = (35,9 - 1,04 · t) · 0,0528 · 1,013t An = (44,2 - 0,51 · t) · 0,0528 · 1,013t Hierin is Ai het aantal mensen (in miljarden) dat in extreme armoede leeft bij gebruik van de internationale armoedegrens, An het aantal mensen (in miljarden) dat in extreme armoede leeft bij gebruik van de nationale armoedegrens en t het aantal jaren na 1990. Er komt een moment waarop er geen mensen meer in extreme armoede leven, wanneer je uitgaat van de formule van Ai . |
|||||||||||||||||||||||||||||||||||||||||||||||
| 5p. | 15. | Bereken hoeveel jaar na 1990 dit het geval is en bereken hoeveel miljard mensen er dan volgens de formule van An nog wel in extreme armoede leven. Geef je antwoord in een geheel aantal jaren en een geheel aantal miljarden. | |||||||||||||||||||||||||||||||||||||||||||||
| Eurobankbiljetten. | ||||||||||||
| In
opdracht van De Nederlandsche Bank is in februari 2023
onderzocht hoe (volwassen) Nederlanders het uiterlijk van
(euro)bankbiljetten waarderen. Het onderzoek is uitgevoerd
door middel van telefonische interviews. Er zijn daarvoor
20823 telefoonnummers willekeurig door een computer bedacht.
Daarvan bleek 51% geen gehoor te geven, in gesprek te zijn
of er was sprake van een niet bestaand nummer. De resterende
telefoonnummers leverden 1003 deelnemers op die meegedaan
hebben aan het telefonisch interview. De 1003 deelnemers vormen op deze manier een steekproef uit de populatie Nederlanders. |
||||||||||||
| 2p. | 16. | Is hier sprake van een aselecte steekproef? Licht je antwoord toe. | ||||||||||
| Bij de deelnemers aan het telefonisch interview werd gevraagd naar een aantal kenmerken (statistische variabelen) zoals | ||||||||||||
| - | het geslacht, | |||||||||||
| - | de leeftijd (in jaren), | |||||||||||
| - | het aantal leden van het huishouden, | |||||||||||
| - | het wel of niet beroepsmatig omgaan met bankbiljetten, | |||||||||||
| - | de provincie waarin men woont, | |||||||||||
| 2p. | 17. | Geef aan welke van de hierboven genoemde variabelen nominaal zijn. | ||||||||||
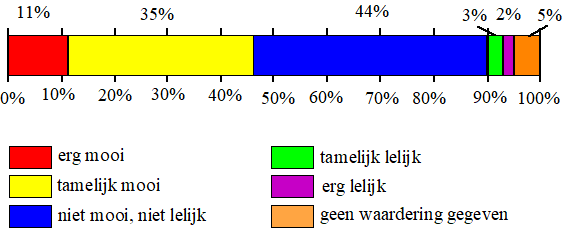
| In het onderzoek is ook gevraagd naar de waardering van de bankbiljetten. Zie de figuur voor het resultaat. | ||||||||||||
|
|
||||||||||||
| Je kunt met de gegevens in de figuur berekenen hoeveel procent van de deelnemers die wel hun waardering van de bankbiljetten hebben gegeven, de bankbiljetten ‘erg mooi’ of ‘tamelijk mooi’ vindt. | ||||||||||||
| 2p. | 18. | Bereken dit percentage in één decimaal. | ||||||||||
| Ook in andere jaren is er onderzoek gedaan naar de waardering van bankbiljetten. In de rest van deze opgave gaan we ervan uit dat alle onderzoeken naar de waardering van de bankbiljetten representatief zijn voor Nederlanders. Om de waardering van de bankbiljetten te meten, gebruikt men de volgende formule om het percentage ‘mooi’ (Pmooi ) te berekenen: | ||||||||||||
|
|
||||||||||||
| In deze
formule staat bijvoorbeeld aantal ‘erg mooi’ voor het aantal
onderzoeksdeelnemers dat aangeeft de bankbiljetten ‘erg
mooi’ te vinden. In 2002 was Pmooi gelijk aan 65. Met de gegevens in de figuur over het onderzoek onder de 1003 deelnemers in 2023 en de formule kunnen we nu Pmooi in 2023 en in 2002 vergelijken. |
||||||||||||
| 4p. | 19. | Bereken het verschil tussen Pmooi in 2023 en Pmooi in 2002. Geef je antwoord in hele procenten. | ||||||||||
| Stel dat een aantal van de onderzoeksdeelnemers die geen waardering hebben gegeven voor de bankbiljetten, bij een heroverweging toch beslissen de bankbiljetten ‘tamelijk lelijk’ te vinden, en dat de overige deelnemers bij hun standpunt blijven. Dan zal de waardering van de bankbiljetten afnemen. | ||||||||||||
| 3p. | 20. | Beredeneer, zonder gebruik te maken van getallenvoorbeelden, dat Pmooi volgens de formule in dit geval inderdaad afneemt. | ||||||||||
| De 1003 deelnemers aan het onderzoek in 2023 zijn op basis van het kenmerk ‘wel of niet beroepsmatig omgaan met bankbiljetten’ onderverdeeld in de groepen A en B. Zie de tabel. | ||||||||||||
|
||||||||||||
| Er blijkt een verschil te bestaan tussen groep A en B: 50% van de deelnemers in groep A en 61% van de deelnemers in groep B verwacht dat er over vijf jaar minder met contant geld betaald zal worden. | ||||||||||||
| 5p. | 21. | Onderzoek met behulp van het formuleblad of dit verschil in verwachting groot, middelmatig of gering is. | ||||||||||
| Topinkomens | |||
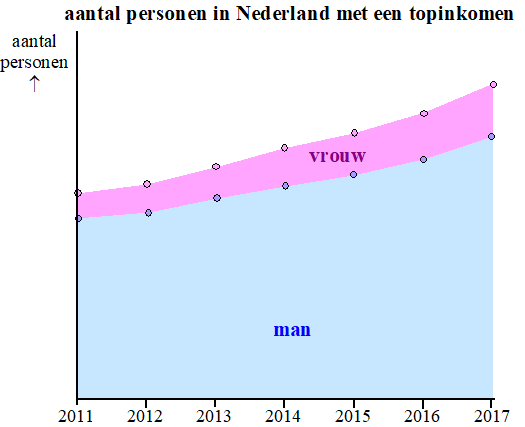
| Er is sprake van een topinkomen als het inkomen van iemand in een jaar (gemeten op 31 december) 100000 euro of meer is. Het aantal personen met zo’n topinkomen in Nederland is vanaf 2011 sterk toegenomen, zie de figuur. | |||
|
|
|||
| In
2017 waren er 13,4 miljoen personen in Nederland met een
inkomen. Daarvan hadden er 360 000 een topinkomen. Dat
waren 120 000 personen meer dan in 2011. Het aantal
vrouwen met een topinkomen groeide in de periode
2011-2017 relatief sterker dan het aantal mannen met een
topinkomen. In 2011 waren er zeven keer zoveel mannen
als vrouwen met een topinkomen. In 2017 was dat nog maar
vijf keer zoveel. Neem aan dat zowel het aantal mannen met een topinkomen als het aantal vrouwen met een topinkomen groeide met een vast percentage per jaar in de periode 2011-2017 en dat deze groei zich voortzet in de jaren na 2017. |
|||
| 8p. | 22. | Onderzoek in welk jaar er in Nederland voor het eerst minder dan drie keer zoveel mannen als vrouwen met een topinkomen zijn. | |