HAVO WA, 2025 - I
CO2 en andere broeikasgassen.
       
In discussies over het klimaat gaat het vaak over de uitstoot van broeikasgassen. In het Nederlandse klimaatakkoord is als doel gesteld dat de gemiddelde uitstoot van broeikasgassen per inwoner per jaar in 2030 gehalveerd is ten opzichte van 1990. In 1990 was in Nederland de gemiddelde uitstoot van broeikasgassen per inwoner per jaar 15,1 ton en in 2017 was die 11,6 ton. Neem aan dat er in de periode 1990-2017 sprake was van een lineaire daling en dat deze daling zich op dezelfde wijze voortzet na 2017.
       
4p. 1. Onderzoek met bovenstaande gegevens en aannames of de genoemde doelstelling gehaald wordt.
     

 
CO2 heeft het grootste aandeel in de broeikasgassen die worden uitgestoten. In de volgende figuur staat de wereldwijde uitstoot van CO2 per jaar.
       

       
Neem aan dat de wereldwijde uitstoot van CO2 in de periode van 1900 tot 1980 exponentieel is gegroeid.
       
5p. 2. Bereken met de gegevens van 1900 en 1980 in de figuur het jaarlijkse groeipercentage in deze periode. Geef je antwoord in één decimaal.
     

 
In onderstaande figuur staat de top zes van landen met de grootste CO2-uitstoot in 2017. In deze opgave beschouwen we de Europese Unie als één land.
       

       
In de volgende figuur staat van dezelfde landen de uitstoot van overige broeikasgassen in 2017 weergegeven.
       

       
Om de totale uitstoot van broeikasgassen in 2017 van deze landen eerlijk te kunnen vergelijken, wordt er rekening gehouden met het aantal inwoners van elk land. Zo kun je van deze landen een ranglijst maken op basis van de gemiddelde uitstoot van alle broeikasgassen per inwoner per land.

Om de ranglijst te kunnen maken, zijn de getallen in de onderstaande tabel nodig, maar voor China ontbreekt nog de gemiddelde uitstoot van alle broeikasgassen per inwoner in 2017.
       
land aantal inwoners
in 2017 (in
miljarden)		 gemiddelde uitstoot van
alle broeikasgassen per
inwoner in 2017 (in ton)
Japan 0,127 11,8
Rusland 0,145 16,6
Verenigde Staten 0,326 20,2
Europese Unie 0,511 9,2
India 1,339 2,7
China 1,386 ....
       
4p. 3. Bereken voor China de gemiddelde uitstoot van alle broeikasgassen per inwoner in 2017 en geef de ranglijst op basis van de gemiddelde uitstoot.
     

 
India brengt de uitstoot van broeikasgassen ook in verband met de omvang van het bruto nationaal product van het land.

Neem aan dat voor India de volgende formules gelden:

     U = 3,6  · 1,02t
     B = 1,34 + 0,01 · t
     BNP = 2597 · 1,06t

Hierin is:
- U de uitstoot van alle broeikasgassen (in miljard ton)
- B het aantal inwoners (in miljarden)
- BNP het bruto nationaal product (in miljard US-dollar)
- t het geheel aantal jaren na 2017

De uitkomsten van de formules gelden telkens op het einde van het jaar. Volgens deze formules zal in India de gemiddelde uitstoot van alle broeikasgassen per inwoner (U/B ) in de jaren na 2017 steeds stijgen. Er komt dan een moment waarop U/ B voor het eerst verdubbeld zal zijn ten opzichte van de waarde in 2017.
       
5p. 4. Bereken in welk jaar dat voor het eerst zal zijn.
     
De gemiddelde uitstoot van alle broeikasgassen per US-dollar bruto nationaal product ( U/BNP ) laat een dalende trend zien na 2017.
       
3p. 5. Beredeneer dit aan de hand van de gegeven formules, zonder hierbij gebruik te maken van getallenvoorbeelden of van een schets of tekening van de grafiek van U/BNP .
     

 
Grut van Grutto's
       
De grutto is een weidevogel. Het vrouwtje maakt een nestkuil in het gras en legt daarin haar eieren. Daarna broeden het mannetje en het vrouwtje om beurten. De eieren komen na ongeveer 24 dagen uit.

Als de grutto’s tijdens het broeden lastiggevallen worden door andere dieren, bijvoorbeeld een vos of een roofvogel, dan verlaat het broedpaar het nest. Dagelijks gaat hierdoor ongeveer 2% van de nesten verloren.
     
3p. 6. Bereken hoeveel procent van de nesten in 24 dagen verloren gaat. Geef je antwoord in hele procenten.
     

 
24 dagen na het uitkomen van het ei is een kuiken vliegvlug. Dit betekent dat de donsveren hebben plaatsgemaakt voor echte veren en dat het kuiken kan vliegen.

Voor het gewicht van kuikens die opgroeien, geldt in de periode vanaf het uitkomen van het ei tot het moment dat het kuiken vliegvlug is, bij benadering:
       

       
Hierin is d het aantal hele dagen na de dag dat het ei uitkwam en G het gewicht van het kuiken in grammen.
       
3p. 7. Bereken hoeveel keer zo zwaar een kuiken is op de dag dat het vliegvlug is, ten opzichte van de dag dat het ei uitkwam. Geef je antwoord als geheel getal.
     

 
We kijken nu naar de gewichtstoename per dag van de kuikens. Er geldt bij benadering:
       

T = 3000 - 0,6G2 + 152,9G       (formule 2)
       
Hierin is G het gewicht van het kuiken in grammen en T de gewichtstoename per dag in milligrammen.
       
5p. 8. Bereken hoeveel dagen na de dag dat het ei uitkwam (d ) de gewichtstoename per dag (T ) van het kuiken maximaal is. Geef je antwoord in gehele dagen.
     

 
In grasland vinden de grutto’s veel prooien, zoals insecten. Naarmate de grutto’s ouder worden, kunnen ze steeds grotere prooien vangen. De grootte van een prooi wordt gegeven in milligram droge stof. Voor de maximale grootte van een prooi die grutto’s kunnen eten, geldt de formule:
       

       
Hierin is P de maximale grootte van de prooi in milligram droge stof en d het aantal hele dagen na de dag dat het ei uitkwam.

De maximale grootte van de prooi die een grutto kan eten, nadert op den duur naar een bepaalde waarde.
       
3p. 9. Beredeneer met behulp van formule 3 welke waarde dit is.
     

 
In vochtig grasland leven meer insecten en andere prooien voor grutto’s dan in droog grasland. Er is onderzoek gedaan naar de grondwaterstand in graslanden met een afnemend aantal grutto’s en naar de grondwaterstand in graslanden met een stabiel aantal grutto’s. De grondwaterstand is de hoogte van het grondwater ten opzichte van het grasoppervlak. De resultaten zijn in onderstaande boxplots verwerkt.
       

 
       
Iemand trekt op basis van dit onderzoek twee conclusies:
  I Er is volgens de vuistregels op het formuleblad een groot verschil tussen de grondwaterstand in graslanden met een afnemend aantal grutto’s en de grondwaterstand in graslanden met een stabiel aantal grutto’s.
  II De grondwaterstand in graslanden met een afnemend aantal grutto’s is normaal verdeeld.
       
4p. 10. Leg voor elk van deze twee conclusies uit of je die wel of niet kunt trekken op basis van de figuur.
     

 
Het gaat niet zo goed met de grutto. Sinds 1990 daalt het aantal grutto’s exponentieel. Twee instanties deden een uitspraak over deze daling: 
  - Een onderzoeksinstituut gaf aan dat in de periode 1990-2019 het aantal grutto’s elke 13 jaar halveerde.
  - Vogelbescherming Nederland gaf aan dat het aantal grutto’s met twee derde was afgenomen in de periode 1990-2019.
       
5p. 11. Onderzoek welke uitspraak leidt tot het hoogste aantal grutto’s in 2019: die van het onderzoeksinstituut of die van Vogelbescherming Nederland.
     

 
Mantelzorgers.
       
Steeds meer ouderen in Nederland blijven langer thuis wonen. Veel ouderen hebben daarbij wel vaak meer zorg nodig. Behalve professionele hulp hebben de meeste ouderen ook mantelzorgers die hen helpen. Mantelzorgers zijn mensen, meestal familieleden, die onbetaald zorg verlenen.

We bekijken de leeftijden van de mantelzorgers. In figuur 1 staan de resultaten uit een representatieve steekproef onder 2749 mantelzorgers van 18 jaar en ouder die zorg verlenen aan ouderen van 85 jaar en ouder.
       

       
Op basis van bovenstaande gegevens kun je voor het percentage 50-74-jarigen in de populatie mantelzorgers van 18 jaar en ouder een 95%-betrouwbaarheidsinterval opstellen.
       
3p. 12. Stel met behulp van het formuleblad dit 95%-betrouwbaarheidsinterval op voor de populatieproportie. Geef de grenzen van het interval als percentages in één decimaal.
     

 
We bekijken twee categorieën ouderen:
-   jongere ouderen: 50 tot en met 74 jaar oud
-   oudere ouderen: 85 jaar en ouder
       
Elke jongere oudere is een potentiële mantelzorger. Om het aantal potentiële mantelzorgers per oudere oudere in beeld te brengen, gebruikt men de maatstaf Oldest Old Support Ratio (OOSR); in formulevorm:
       

       
Sinds 1975 neemt de OOSR op landelijk niveau af. Ten opzichte van 1975 is het aantal jongere ouderen in 2015 met 25% toegenomen. In diezelfde periode is het aantal oudere ouderen tweeënhalf keer zo groot geworden.
       
3p. 13. Bereken met hoeveel procent de OOSR in 2015 ten opzichte van 1975 is afgenomen.
     

 
Omdat mantelzorgers meestal in de buurt van oudere ouderen wonen, wordt de OOSR ook per gemeente berekend. We vergelijken de OOSR van twee gemeenten met behulp van bevolkingsdiagrammen. Een bevolkingsdiagram is een diagram waarin aan twee kanten de leeftijdsopbouw van de bevolking is weergegeven, links die van de mannen en rechts die van de vrouwen. In onderstaande figuur zie je twee bevolkingsdiagrammen (I en II) waarvan er één bij gemeente A hoort en de ander bij gemeente B. Daarbij geldt dat de OOSR van gemeente A groter is dan die van gemeente B.
       

       
4p. 14. Beredeneer welk bevolkingsdiagram bij gemeente A hoort.
     

 
In onderstaande figuur zijn van alle gemeenten de OOSR’s verwerkt in boxplots voor de jaren 2015 en 2020.
       

       
We kijken in deze figuur naar de gemeenten die een OOSR van minder dan 16 hebben. Iemand beweert dat het aantal gemeenten met deze eigenschap in de periode 2015-2020 met een kwart van het totaal aantal gemeenten is toegenomen.
       
3p. 15. Beredeneer met behulp van deze figuur of deze bewering juist is.  
     

 
Als thuis wonen zelfs met hulp van professionals en mantelzorgers niet meer mogelijk is, kunnen mensen in een zorginstelling gaan wonen. Mantelzorgers krijgen dan minder zorgtaken, maar blijven noodzakelijk om bijvoorbeeld de financiën te regelen. Een zorginstelling wil weten wat de bewoners en hun mantelzorgers vinden van de zorg die de zorginstelling biedt. Daarom wordt er een representatieve steekproef genomen uit de bewoners en hun mantelzorgers. De deelnemers aan de steekproef gaven antwoord op de vraag:

In hoeverre bent u tevreden over de geboden zorg?

De uitkomsten van de steekproef staan in de volgende figuur.
       

       
3p. 16. Geef aan van welke twee variabelen er sprake is in dit onderzoek en geef bij elk van deze twee variabelen aan of het een nominale of ordinale variabele is. Licht je antwoord toe.
     

 
4p. 17. Onderzoek met behulp van het formuleblad of het verschil in de mate van tevredenheid tussen bewoners en mantelzorgers groot, middelmatig of gering is.
     

 
Hoe zwaar is een bergbeklimming met de fiets?
       
Elke zomer zijn er heel wat Nederlandse wielrenners te vinden op bergwegen in Frankrijk. Deze hele opgave gaat over bergbeklimmingen met de fiets. Er bestaat een model waarmee de zwaarte van een bergbeklimming met de fiets, berekend kan worden. Volgens dit model geldt:
     

     
Hierin is:
  - I de zwaarte-index  
  - h het hoogteverschil tussen begin- en eindpunt van de beklimming (in meter)
  - w de weglengte die tijdens de beklimming wordt afgelegd (in kilometer)
       
Voor de beklimming van de Franse berg Mont Ventoux geldt een zwaarte-index van 12,1.
In Nederland bevindt zich de Vaalserberg. Bij de beklimming van deze berg vanuit het dorp Vaals leg je 2830 meter af om de top te bereiken. Het hoogteverschil bij deze beklimming is 143 meter.
       
3p. 18. Bereken hoeveel keer zo groot de zwaarte-index van de beklimming van de Mont Ventoux is als die van de beklimming van de Vaalserberg. Geef je antwoord als geheel getal.
     

 
De beklimming van de Franse berg Alpe d’Huez start vanuit het dorpje Bourg d’Oisans op een hoogte van 799 meter. Het eindpunt ligt op een hoogte van 1860 meter. De zwaarte-index van deze beklimming is 9,2.
       
4p. 19. Bereken de weglengte van deze beklimming. Geef je antwoord in gehele kilometers.
     

 
Formule 1 kan worden herleid tot de vorm:   h = 100·Ö(w · I)      (formule 2)
       
2p. 20. Geef deze herleiding.
     

 
Iemand zoekt een bergbeklimming met een maximale weglengte van 4 km. De zwaarte-index moet tussen die van de Alpe d’Huez (9,2) en die van de Mont Ventoux (12,1) in liggen. Om zo’n bergbeklimming te vinden, geeft hij met behulp van formule 2 in een assenstelsel het gebied aan met de combinaties van w en h die leiden tot een dergelijke I. Hieronder is het assenstelsel al getekend.
       

       
3p. 21. Teken in het assenstelsel het juiste gebied.
     

 
Zorg om zorguitgaven.
       
In Nederland regelt de Zorgverzekeringswet (Zvw) een verplichte basisverzekering voor alle inwoners. Deze basisverzekering dekt de zorguitgaven aan huisartsen en de zorguitgaven aan specialisten; de som hiervan noemen we de totale zorguitgaven. In 2018 bedroegen de totale zorguitgaven 19,637 miljard euro.

Uit onderzoek blijkt dat er een samenhang bestaat tussen de zorguitgaven aan huisartsen en de zorguitgaven aan specialisten. Als huisartsen meer mogelijkheden krijgen om hun patiënten te helpen, worden de zorguitgaven aan huisartsen hoger en de zorguitgaven aan specialisten lager. In deze opgave onderzoeken we of extra uitgaven aan huisartsenzorg leiden tot lagere totale zorguitgaven als we uitgaan van bepaalde gegevens en aannames.

We bekijken het jaar 2018 en gebruiken de volgende gegevens:
    Er waren 17 miljoen verzekerden die onder de Zvw vielen.
    Alle 17 miljoen verzekerden stonden ingeschreven bij een huisarts.
    30% van alle verzekerden kreeg van de huisarts een verwijzing naar een specialist.
    In de tabel staan de gemiddelde zorguitgaven per verzekerde zonder of met verwijzing naar een specialist.
       
gemiddelde zorguitgaven per verzekerde
zonder of met verwijzing naar een specialist (in euro's)
  gemiddelde
zorguitgaven
aan huisartsen		 gemiddelde
zorguitgaven
aan specialisten		 gemiddelde
totale
zorguitgaven
verzekerde
zonder verwijzing
naar een specialist
(70%)		 43 0 43
verzekerde
met verwijzing
naar een specialist
(30%)		 250 3500 3759
       
We nemen aan dat in 2018 voor de verzekerden met een verwijzing naar een specialist, elke stijging van 10 euro op de gemiddelde zorguitgaven aan huisartsen leidt tot een daling van 0,5% van hun gemiddelde zorguitgaven aan specialisten. Dus als bijvoorbeeld de 250 euro in de tabel zou stijgen naar 260 euro, dan zou de 3500 euro in de tabel met 0,5% dalen naar 3482,50 euro.

Stel nu dat in 2018 de zorguitgaven aan huisartsen van verzekerden met een verwijzing naar een specialist in totaal 510 miljoen euro hoger zouden zijn.
       
6p. 22. Onderzoek aan de hand van bovenstaande gegevens en aannames of de totale zorguitgaven in 2018 dan lager zouden zijn dan 19,637 miljard euro.
     

 
UITWERKING
   
Het officiële (maar soms beknoptere) correctievoorschrift kun je HIER vinden. Vooral handig voor de onderverdeling van de punten.
   
1. Er is een daling van 15,1 - 11,6 = 3,5 ton in 27 jaar.
Per jaar is dat  3,5/27 =
0,1296... ton
2017 tot 2030 is nog 13 jaar.
dat zou een daling van 13 · 0,1296... = 1,6851... ton geven
11,6 - 1,6851... = 9,91 ton
dat is meer dan de helft van 15,1 ton dus de doelstelling is dan WEL gehaald.
   
2. aflezen uit de figuur:  (1900, 2.5 )  en  (1980, 18)
de groeifactor daartussen is  18/2,5 = 7,2
Dat is in 80 jaar dus per jaar is de groeifactor  7,21/80 = 1,0249...
dat is een groei van 2,5%
   
3. aflezen:  de totale uitstoot van China is 10,9 CO2 en 2,6 overige
samen is dat 13,5
per inwoner is dat  13,5/1,386 = 9,74 ton per inwoner

de volgorde wordt dan:
Verenigde Staten, Rusland, Japan, China, Europese Unie, India
   
4. Zet U/B in de GR:
Y1 = (3,6  * 1,02^X)/(1,34 + 0,01X)
Aflezen in de tabel :  X = 0 geeft  Y = 2,68656...  Dus verdubbelen geeft Y = 5,37...
Y2 = 5,37
intersect geeft dan X = 51,35...

Dat is voor het eerst in 2069.
   
5. U/BNP = (3,6  · 1,02t) / (2597 · 1,06t)
De teller en de noemer zijn beiden een exponentiële formule
De noemer heeft een grotere groeifactor dan de teller.
Dus de noemer stijgt sneller dan de teller.
Dan wordt de hele breuk kleiner.
   
6. 2% afname betekent per dag een groeifactor van 0,98
in 24 dagen is dat 0,9824 = 0,6158
dus 62% blijft over
dat is een afname van 38%
   
7. d = 0 invullen  geeft  G =  20,....
d = 24 invullen  geeft  G =  239,....
dat is dus  239/20 = 11,9  dus 12 keer zo zwaar.
   
8. Y1 = 3000 - 0,6X^2 + 152,9*X
calc - maximum geeft  X = G = 127,41664...

Y1 = 273/(1,08 + 12,5*0,8^X)
Y2 = 127,41664
intersect geeft   X = d =  11,046... 
Dat is dus na 11 dagen.  
   
9. Als d alsmaar groter wordt:
dan wordt d - 14,69 ook alsmaar groter
dan wordt  0,74d - 14,69  steeds kleiner (want 0,74 < 1):  dat gaat naar nul toe
dan gaat de noemer van de formule naar 1
dan gaat de breuk naar 2,15
dan gaat P naar 3,459
   
10. De boxen van de boxplots overlappen elkaar niet, dus het verschil is groot.
Conclusie I kun je wel trekken.

De boxplot van het afnemend aantal grutto's is niet symmetrisch (want de mediaan ligt niet in het midden van de box) en dat zou bij een normale verdeling wel zo moeten zijn.
Conclusie II kun je niet trekken.
   
11. halveren betekent een groeifactor van 0,5
Dat is in 13 jaar dus per jaar is  g = 0,51/13 = 0,948...
1990 naar 2019 is 29 jaar
dat geeft ene groeifactor van  0,948...29 = 0,213...
de groeifactor volgens Vogelbescherming is 1/3 (want de afname is 2/3) en dat is meer dan 0,213
dus volgens de Vogelbescherming zijn er het hoogste aantal grutto's.
   
12. aflezen:  het percentage 50-74 jarigen is  88 - 28 = 60%
dus de proportie is p = 0,60
n = 2749
Ö(0,6 · 0,4/2749) = 0,0093
0,6 + 2 · 0,0093 = 0,6186
0,6 - 2 · 0,0093 = 0,5814
het 95%-betrouwbaarheidsinterval is  [58.1  ; 61.9]
   
13. noem het aantal jongere ouderen J en het aantal oudere ouderen O
dan is J met 25% toegenomen dus Jnieuw = 1,25Joud
O is 2,5 keer zo groot geworden, dus  Onieuw = 2,5Ooud 
 
  Dus OOSR is met 50% afgenomen.
   
14. Bevolkingsdiagram I heeft minder oudere ouderen dan bevolkingsdiagram II
Bevolkingsdiagram I heeft meer jongere ouderen dan bevolkingsdiagram II
Hoe kleiner het aantal oudere ouderen ten opzichte van het aantal jongere ouderen, hoe hoger de OOSR
Dus bevolkingsdiagram I hoort bij gemeente A
   
15. In 2015 heeft 50% van die gemeenten een OOSR van minder dan 16  (nl. twee kwartielen)
In 2020 heeft 75% van die gemeenten een OOSR van minder dan 16 (nl. drie kwartielen)
Het gaat in beide jaren om hetzelfde aantal gemeenten dus de procenten geven dezelfde echte aantallen weer.
dus de bewering is juist
   
16. de variabelen zijn  "mate van tevredenheid"  en  "soort deelnemer"
beiden zijn kwalitatief.
in de mate van tevredenheid zit een volgorde, dus die variabele is ordinaal
in soort deelnemer zit geen volgorde dus die variabele is nominaal.
   
17. percentages aflezen:
 
  bewoners mantelzorgers
mate van tevredenheid    
slecht 0 1
onvoldoende 3 1
voldoende 19 27
goed 35 56
uitstekend 43 15
  maak er cumulatieve percentages van:
 
  bewoners mantelzorgers
mate van tevredenheid   cumulatief   cumulatief
slecht 0 0 1 1
onvoldoende 3 3 1 2
voldoende 19 22 27 29
goed 35 57 56 85
uitstekend 43 100 15 100
   
  |De verschillen tussen de cumulatieve percentages zijn:  1 - 1 - 7 - 28 - 0
Het maxVcp  is dus 28%
Dat zit tussen 20 en 40 dus het verschil is middelmatig.
   
18. Vaalserberg: 
h = 143
w = 2,83
I = 143²/(10000 · 2,83)= 0,722...
12,1/0,722... = 16,7
De zwaarte-index van de Mont-Ventoux is 17 keer zo groot als die van de Vaalserberg.
   
19. h = 1860 - 799 = 1061
I = 9,2
invullen:  9,2 = 1061²/(10000w) 
Y1 = 1061^2/(10000X)
Y2 = 9,2
intersect geeft  X = w = 12 km
   
20.
vermenigvuldig beide kanten met 10000w
dat geeft  I · 10000w = h2
neem nu van beide kanten de wortel:
h = Ö(10000wI)
h =  Ö(10000) · Ö(wI)
h = 100Ö(wI)
   
21. teken de grafieken van  h = 100Ö(9,2w)  en  h = 100Ö(12,1w):
 
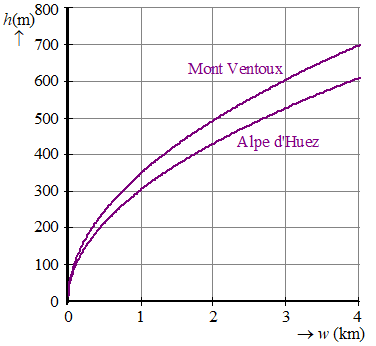  Het gezochte gebied is het gebied tussen beide grafieken in.
   
22. Het aantal verzekerden met een verwijzing is 30% van 17 miljoen, dus  0,3 · 17 =  5,1 miljoen
Voor deze verzekerden worden de gemiddelde zorguitgaven aan huisartsen 510/5,1  = 100
Dit leidt tot 100/10 = 10 (euro) per verzekerde hoger
Dus 10 keer een verlaging met 0,5% van de gemiddelde zorguitgaven aan specialisten per verzekerde met verwijzing
Een verlaging met 0,5% betekent een groeifactor 0,995.
De gemiddelde zorguitgaven aan specialisten per verzekerde met verwijzing worden
0,99510 · 3500 = 3328,8...) (euro)
De daling van de gemiddelde zorguitgaven aan specialisten per verzekerde met verwijzing is 3500 - 3328,8 = 171,11...(euro)
Deze daling (171,11 euro) is hoger dan de stijging (100 euro) dus de totale zorguitgaven zouden dan lager zijn.