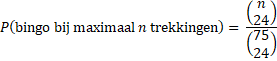| Huishoudelijke apparaten. | |||
|
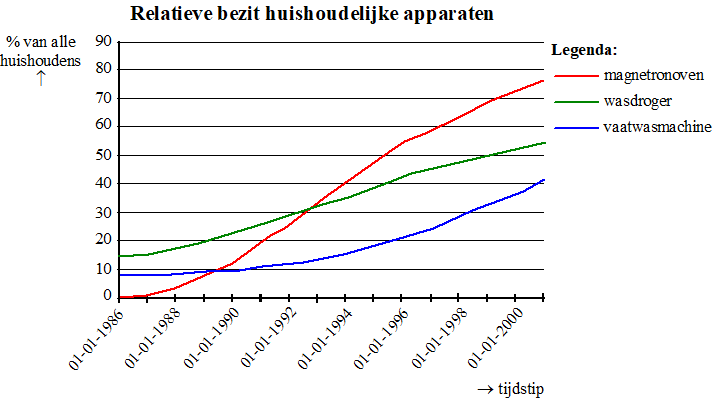
In elk huishouden is wel een aantal huishoudelijke apparaten te vinden. Uit een onderzoek van het CBS (Centraal Bureau voor de Statistiek) in 2003 blijkt dat het bezit van bijvoorbeeld magnetronovens, wasdrogers en vaatwasmachines sterk toenam in de periode 1986–2001. Zie de volgende figuur. |
|||
|
|
|||
|
Deze opgave gaat over het relatieve bezit: het
bezit, uitgedrukt als percentage van het totale aantal huishoudens. Op grond van de grafiek kun je concluderen dat er op 1 januari 1998 huishoudens waren die zowel een magnetronoven als een wasdroger bezaten. |
|||
| 3p. |
1. |
Leg dat uit. | |
|
Uit het onderzoek blijkt dat het relatieve bezit van wasdrogers op 1 januari 1986 14,4% was. Op 1 januari 2001 was het toegenomen tot 54,4%. Omdat uit de figuur blijkt dat er sprake is van vrijwel lineaire groei in deze periode, kunnen we voor deze periode aan de hand van deze gegevens de volgende formule opstellen: W = a • t + 14,4Hierin is W het relatieve bezit van wasdrogers en t de tijd in jaren, waarbij t = 0 overeenkomt met 1 januari 1986. |
|||
| 3p. |
2. |
Laat met een berekening zien dat a afgerond 2,67 is. | |
|
Uit het onderzoek blijkt verder dat het relatieve bezit
van vaatwasmachines op 1 januari 1986 8,0% was en op 1 januari 2001
41,6%. We gaan ervan uit dat de groei exponentieel verliep. |
|||
| 4p. |
3. |
Toon aan dat de jaarlijkse groeifactor (ongeveer) 1,116 is. | |
|
We kunnen nu voor het relatieve bezit van vaatwasmachines de volgende formule opstellen: V = 8,0 • 1,116tHierin is V het relatieve bezit van
vaatwasmachines en t de tijd in jaren, waarbij t = 0
overeenkomt met 1 januari 1986. W = 2,67 • t + 14,4 en V = 8,0 • 1,116t |
|||
| 4p. |
4. |
Bereken met behulp van de twee formules in welk jaar het relatieve bezit van wasdrogers en vaatwasmachines even groot is. |
|
|
Koelkasten zijn veel algemener in gebruik in Nederlandse huishoudens dan de apparaten die we eerder in deze opgave bekeken. Het aantal koelkasten is al tientallen jaren gelijk aan 97% van het aantal huishoudens, terwijl het aantal huishoudens al jarenlang lineair stijgt. Met gegevens van het CBS is voor het aantal huishoudens H (in duizendtallen) de volgende formule opgesteld: H = 69,8 • t + 5790In deze formule is H dus het aantal huishoudens
in duizendtallen en t in jaren met t = 0 op 1 januari
1986. |
|||
| 4p. |
5. |
Bereken a en b. | |