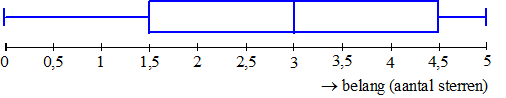Nieuwe pagina 1

HAVO WA, 2016 - I. PILOT

Vertrouwen.

Het Sociaal en Cultureel Planbureau beschrijft om de twee jaar in het rapport 'De Sociale Staat van Nederland' hoe het met het vertrouwen van Nederlanders gesteld is. Daarbij wordt onder andere onderscheid gemaakt tussen het vertrouwen in de medemens, ook wel het sociale vertrouwen genoemd, en het vertrouwen in het parlement. Beide soorten van vertrouwen worden uitgedrukt in een percentage: hoe hoger het percentage, des te meer vertrouwen. In de figuur wordt het vertrouwen van Nederlanders in het jaar 2008 vergeleken met dat van andere Europeanen. Je kunt bijvoorbeeld aflezen dat in Italië het sociale vertrouwen 30% bedroeg.



In de figuur is af te lezen hoe groot in Nederland het vertrouwen in het parlement was. In sommige van de overige landen was het vertrouwen in het parlement groter.

3p.	1.	Bepaal in hoeveel procent van de overige landen dit het geval was.

3p.	2.	Schrijf de namen op van alle landen waar het sociale vertrouwen groter was dan het vertrouwen in het parlement.

Voor het onderzoek 'Sociale samenhang' in 2013 werden gegevens verzameld onder de Nederlandse bevolking. Er deden 7400 aselect getrokken personen aan dit onderzoek mee. Van de deelnemers gaven 4292 personen aan vertrouwen te hebben in de medemens. Op basis van deze gegevens worden de volgende twee uitspraken gedaan over het percentage Nederlanders dat (in 2013) vertrouwen had in de medemens:
1.	Het is meer dan 95% zeker dat het percentage Nederlanders dat vertrouwen had in de medemens, in het interval [56,6 ; 59,4] ligt.
2.	Het is minder dan 95% zeker dat het percentage Nederlanders dat vertrouwen had in de medemens, in het interval [56,6 ; 59,4] ligt.

Eén van deze twee uitspraken is juist.

4p.	3.	Welke uitspraak is juist? Licht je antwoord met een berekening toe.

Duiken.

Duiken is een mooie sport, maar niet ongevaarlijk. Het grootste gevaar waar duikers mee te maken krijgen, is de druk van het water op het lichaam. Deze druk wordt hoger naarmate de duiker dieper duikt. Een formule die het verband tussen de druk en de diepte weergeeft, luidt: p = 1 + ^d/₁₀ Hierin is p de druk van het water op het lichaam in bar en d de diepte onder water in meter. Duikorganisaties adviseren recreatieve duikers om de druk van het water op het lichaam niet hoger te laten worden dan 5 bar

3p.	4.	Bereken hoe diep een recreatieve duiker dan maximaal kan duiken.

Bij een duik wordt een duikfles meegenomen met perslucht om onder water te kunnen ademen. Perslucht is lucht die onder grote druk wordt samengeperst. De hoeveelheid perslucht L wordt uitgedrukt in barliter. De waarde van L wordt berekend door de inhoud van de fles (in liter) te vermenigvuldigen met de druk (in bar). Als je bijvoorbeeld een duikfles van 15 liter vult tot een druk van 200 bar, dan is de hoeveelheid perslucht in de fles 15 × 200 = 3000 barliter. Om de benodigde hoeveelheid perslucht voor een duik te berekenen, maakt een duiker gebruik van de volgende formule: L = 20 • p • T Hierin is L de hoeveelheid perslucht in barliter, p de druk van het water op het lichaam in bar en T de duiktijd in minuten. De duiktijd is de tijd die de duiker onder water is. Jan wil een duik gaan maken van drie kwartier naar een diepte van 19 meter. Hij gebruikt een duikfles van 12 liter en vult deze tot een druk van 200 bar.

4p.	5.	Bereken of Jan hiermee deze duik kan maken.

Het Grevelingenmeer in de provincie Zeeland is een groot meer, dat niet overal even diep is. Dennis gaat duiken in een gedeelte van dit meer, waar het nergens dieper dan 25 meter is. Hij vult zijn duikfles met 2400 barliter perslucht. Met deze hoeveelheid perslucht heeft Dennis verschillende mogelijkheden voor zijn duik. Hij kan bijvoorbeeld kiezen voor een niet al te diepe duik waarbij hij lang onder water kan blijven, of voor een diepere duik met een kortere duiktijd. Dennis kan voor de keuze van zijn duik een grafiek tekenen, waarbij hij de duiktijd T uitzet tegen de diepte d.

5p.	6.	Teken deze grafiek in de figuur hieronder voor duiken van minstens 5 meter en hoogstens 25 meter diep. Bereken hiervoor eerst voor minstens vijf dieptes d de bijbehorende duiktijd T.

Links naar Wikipedia-artikelen.

Wikipedia is een encyclopedie op internet, waarin veel artikelen over diverse onderwerpen te vinden zijn. In die artikelen wordt vaak met een link verwezen naar andere artikelen. Van elk artikel dat op 24 januari 2009 in het Engelse Wikipedia voorkwam, is onderzocht hoeveel links in andere artikelen naar het betreffende artikel verwezen.
Deze links worden de binnenkomende links genoemd. Het aantal binnenkomende links per artikel is geteld. De resultaten van dit onderzoek staan in de volgende figuur en tabel.

aantal binnenkomende links	aantal artikelen
0	133515
1 of 2	465915
3 tm 10	763683
11 of meer	1212195
totaal	2575308

In het onderzoek valt onder andere het volgende te lezen:
“43% van de artikelen met 11 of meer binnenkomende links heeft zelfs 50 of meer binnenkomende links. Dat zijn de echt belangrijke artikelen, waarnaar vaak verwezen wordt.”

De lange staart van artikelen waarnaar 50 of meer keer verwezen wordt, is niet aangegeven in de figuur. Deze staart hoort er uiteraard wel bij.

3p.

Bereken hoeveel procent van alle artikelen uit het onderzoek 50 of meer binnenkomende links hadden.

De drie centrummaten van het aantal binnenkomende links, namelijk het gemiddelde, de modus en de mediaan, zijn alle drie verschillend.

4p.

Zet de centrummaten op volgorde van klein naar groot. Licht je antwoord toe.

De onderzoekers kwalificeren het belang van elk artikel door het te voorzien van een aantal hele en/of halve sterren.
Artikelen die geen binnenkomende links hebben, zijn volgens hen niet of nauwelijks van belang en krijgen daarom 0 sterren. De belangrijkste artikelen krijgen 5 sterren.

In de tabel hiernaast kun je aflezen welk aantal sterren bij welk aantal binnenkomende links hoort.

In de figuur hieronder is de boxplot getekend die hoort bij het belang, uitgedrukt in het aantal sterren.

4p.

Laat met een berekening zien dat het eerste kwartiel in de boxplot juist is aangegeven.

Bepaalde informatie over het aantal binnenkomende links kan gemakkelijk uit de boxplot in combinatie met tabel 2 afgelezen worden. Voor andere informatie is het oorspronkelijke staafdiagram juist gemakkelijker.

3p.

10.

Geef één voorbeeld van informatie over het aantal binnenkomende links die gemakkelijker uit de boxplot (in combinatie met de tabel) gehaald kan worden. Geef ook twee voorbeelden van informatie die alleen uit het staafdiagram af te lezen is.

Start to run.

Als je begint met hardlopen, moet je in het begin niet te snel of te lang willen lopen. Het is veel beter om rustig aan te beginnen en eerst een goede conditie op te bouwen. Een trainingsprogramma dat veel gebruikt wordt, heet Start to Run. Daarbij moet je tien weken lang drie keer per week hardlopen, waarbij je gaandeweg steeds langere periodes aan één stuk hardloopt. In de figuur zie je hoe het trainingsprogramma eruitziet.

Week- nummer	Trainings- dag	Programma	Totaal aantal minuten

1	1 2 3	+0+0++00++00+++000 +0+0++00+++000+++000 +0++00++00+++000+++000	18 20 22

2	1 2 3	+0++00++00+++000+++000 ++00+++000+++000+++000 +0++00+++000+++000+++000	22 22 24

3 en 4	1 2 3	+0++00+++000+++000+++000 ++00++0++0++0++0++0++0++0 +0++00++++000++++000+++++0	24 25 26

5 en 6	1 2 3	++00+++00+++++000+++++000+++++00 ++0+++00++++++00++++++00+++++++00 ++00++++00+++++00++++++00+++++++00	32 33 34

7	1 2 3	+++++0++++++00+++++++00++++++++0 ++++++++0++++++++00++++++++0++++++++0 ++++++++++00++++++++++00++++++++++++0	32 37 37

8 en 9	1 2 3	+++++++++++++++00+++++++++++++++00 ++++++++++0++++++++++++0++++++++++++0 ++++++++++0++++++++++++++++++++0	34 37 32

10	1 2 3	30 minuten hardlopen met 1 of 2 minuten wandelen naar keuze 32 minuten hardlopen met 1 of 2 minuten wandelen naar keuze 30 minuten hardlopen zonder wandelen	31 of 32 33 of 34 30
+ betekent: 1 minuut hardlopen 0 betekent: 1 minuut wandelen

In het schema kun je aflezen dat je op trainingsdag 1 van week 1 eerst tweemaal om en om één minuut moet hardlopen en één minuut moet wandelen, daarna tweemaal twee minuten moet hardlopen en twee minuten moet wandelen en ten slotte drie minuten moet hardlopen en drie minuten moet wandelen. Daarmee ben je 18 minuten bezig.
Het programma is zo opgesteld dat je na tien weken een halfuur zonder onderbreking kunt hardlopen. Het gaat bij Start to Run niet om de snelheid waarmee je hardloopt, dat komt later. Er wordt juist geadviseerd om gedurende deze tien weken de hardloopsnelheid constant te houden.

Mevrouw Harmsen traint volgens het programma en is inmiddels in week 9. Haar hardloopsnelheid is steeds 140 meter per minuut en haar wandelsnelheid is steeds 50 meter per minuut.

4p.

11.

Teken in onderstaande figuur de grafiek van de afgelegde afstand van mevrouw Harmsen tijdens trainingsdag 1 van week 9.

Meneer Saddal volgt het programma van Start to Run ook. Zijn hardloopsnelheid is gedurende het hele programma 9 km per uur. Dit is tweeënhalf keer zo hoog als zijn wandelsnelheid. Je kunt een formule opstellen voor de totale afstand die meneer Saddal per trainingsdag aflegt. Deze formule luidt:

A = 0,15 • H + 0,06 • W

Hierin is A de totale afgelegde afstand in km, H het aantal hardloopminuten en W het aantal wandelminuten.

3p.

12.

Laat met berekeningen zien dat deze formule juist is.

Meneer Saddal legt op de laatste trainingsdag van week 10, als hij een halfuur lang zonder onderbreking kan hardlopen, een veel grotere afstand af dan op de eerste trainingsdag van week 1.

3p.

13.

Bereken hoeveel meter het verschil is.

Meneer Saddal krijgt de smaak te pakken en gaat na de periode van 10 weken door met hardlopen. Hij besluit om een uur lang te gaan trainen.
Tijdens het hardlopen houdt hij zijn gebruikelijke snelheid aan. Lukt dat niet, dan houdt hij één of meer minuten wandelpauze.
Voor een training van een uur geldt dan:

W = 60 − H

Hierin is W het aantal wandelminuten en H het aantal hardloopminuten.
Als je de formule van W invult in de formule van A, ontstaat een formule van A die alleen nog afhangt van het aantal hardloopminuten H. Deze nieuwe formule van A is te herleiden tot de vorm A = a • H + b , waarbij a en b getallen zijn.

3p.

14.

Herleid de formule van A tot deze vorm.

Opslag van radioactief afval.

Een Gammacell is een apparaat dat onder andere gebruikt wordt bij onderzoek naar de bederfelijkheid van voedsel. De Gammacell is een stalen kast waarin zich de radioactieve stof cesium bevindt. Zie de foto. De hoeveelheid radioactieve straling van cesium neemt jaarlijks met een vast percentage af en is na ongeveer 30 jaar gehalveerd.

4p.	15.	Bereken met hoeveel procent de hoeveelheid radioactieve straling per jaar afneemt.

De tijd waarin de hoeveelheid straling tot de helft is afgenomen, wordt de halveringstijd genoemd. Soms wordt de volgende vuistregel gebruikt: 'Na tien keer de halveringstijd is het radioactieve materiaal zijn straling kwijt.' Volgens deze vuistregel zou cesium dus na 300 jaar zijn straling kwijt zijn. Dat is niet helemaal juist. Er is nog een klein beetje van de beginstraling over.

3p.	16.	Bereken hoeveel procent van de beginstraling er na 300 jaar nog over is.

De stalen wand van de kast, waarin zich de stof cesium bevindt, houdt veel van de radioactieve straling tegen. Het deel van de straling dat tegengehouden wordt door de stalen wand, geven we aan met D. Hiervoor geldt de formule:

Hierin is d de dikte van de stalen wand in cm. Je kunt de formule van D schrijven in de vorm D = 1 − g^d , waarbij g een getal is.

3p.	17.	Bereken g en rond je antwoord af op 2 decimalen.


Afgedankte Gammacellen worden verwerkt en opgeslagen door het bedrijf Covra in Borssele. Het bedrijf moet ervoor zorgen dat uit zo’n Gammacell heel weinig straling vrijkomt wanneer deze wordt opgeslagen. Een Gammacell met een stalen wand van 35 cm dik werkt niet goed meer en wordt afgedankt. Je kunt berekenen dat de stalen wand van deze Gammacell 8% van de straling doorlaat die het cesium heeft op het moment dat het bij Covra binnenkomt. Omdat dat percentage voor opslag te veel is, wordt de hele Gammacell ingepakt in beton. Van de straling die door het staal heen komt, wordt een percentage P door het beton doorgelaten. Dit percentage hangt af van de dikte van het beton. Er geldt de formule:



Hierin is d de dikte van het beton in cm. Het bedrijf moet de dikte van het beton zo kiezen, dat het staal en het beton samen 5% van de straling doorlaten die het cesium op het moment van binnenkomst heeft.

5p.	18.	Bereken hoeveel cm de dikte van het beton moet zijn. Rond je antwoord af op een geheel getal.

Door de Westerscheldetunnel.

De Westerscheldetunnel verbindt Zeeuws-Vlaanderen met de rest van Nederland. Voor ieder voertuig, waarmee gebruikgemaakt wordt van de tunnel, moet tol betaald worden. In deze opgave gaan we uit van de tarieven die in 2013 golden per passage (enkele reis). Zie de volgende figuur.



Voor elke categorie bestaan er drie verschillende tarieven:
-	Wie maar af en toe gebruikmaakt van de tunnel, betaalt het standaardtarief.
-	Vaste klanten zijn goedkoper uit: zij bestellen eenmalig gratis de zogenaamde t-tag, een elektronisch apparaat waarmee automatisch wordt betaald. Vervolgens betalen zij bij elke passage het t-tagtarief.
-	Daarnaast krijgen vaste klanten met t-tag nog meer korting indien zij vaak gebruik maken van de tunnel: voor elke passage na de 150^e passage in een kalenderjaar betalen zij het nog lagere veelgebruikerstarief.

Meneer Dingemanse woont in Middelburg en werkt 200 dagen per kalenderjaar in Terneuzen. Op deze dagen maakt hij heen en terug gebruik van de Westerscheldetunnel. Hij rijdt in een personenauto zonder aanhanger. Met de t-tag is hij veel goedkoper uit dan wanneer hij telkens het standaardtarief zou betalen.

4p.	19.	Bereken hoeveel euro hij per kalenderjaar goedkoper uit is met een t-tag.

Voor de bestuurder van een personenauto zonder aanhanger die gebruikmaakt van de t-tag, hangen de totale kosten K in een kalenderjaar af van het aantal passages p in dat jaar. De grafiek van K bestaat uit twee gedeelten, waarbij het tweede gedeelte minder steil loopt. In de figuur hieronder is een schets gemaakt van deze grafiek.



5p.	20.	Stel voor beide gedeelten een formule op voor K, uitgedrukt in p.

Bij het veelgebruikerstarief voor kleine (bestel)bussen hoort vanaf de 150^e passage de formule: K = 11,15 • p + 412,5 Hierin zijn K de kosten in euro’s en is p het aantal passages in een kalenderjaar. De formule geeft de kosten K inclusief 21% btw. In sommige situaties werkt men liever met een formule voor de kosten zonder btw. Deze formule kan worden herleid uit de formule van K en heeft de vorm: K_{zonder btw} = a • p + b Hierin zijn a en b getallen en is p het aantal passages in een kalenderjaar.

3p.	21.	Bereken a en b. Rond je antwoorden af op twee decimalen.

Vrouwenvoetbal.

Vrouwenvoetbal is in. Steeds meer vrouwen en meisjes in Nederland zijn lid van een voetbalclub. In de figuur zie je de ontwikkeling van het aantal vrouwelijke leden van voetbalclubs in de periode 2002 tot en met 2014, telkens gemeten op 1 juli van het betreffende jaar. In de figuur is onder andere te zien dat zowel bij de jeugd als bij de senioren het aantal leden toeneemt. Omdat het aantal leden bij de jeugd sneller groeit dan bij de senioren, wordt het percentage senioren bij de voetbalsters steeds lager. In 2002 was nog iets meer dan 50% van de voetbalsters senior, in 2014 was dat percentage geslonken tot minder dan 40%.



De ontwikkeling van zowel het aantal leden bij de jeugd als bij de senioren is te benaderen door een lineair verband. De bijbehorende lijnen zijn in de figuur weergegeven. We gaan ervan uit dat de aantallen leden van de beide groepen zich volgens de getekende lijnen zullen blijven ontwikkelen. Het percentage senioren zal dan nog verder afnemen. In een bepaald jaar zal op 1 juli het percentage senioren voor het eerst lager zijn dan 35% van het totaal aantal leden.

8p.	22.	Onderzoek in welk jaar dat is.

UITWERKING

Het officiële (maar soms beknoptere) correctievoorschrift kun je HIER vinden. Vooral handig voor de onderverdeling van de punten.

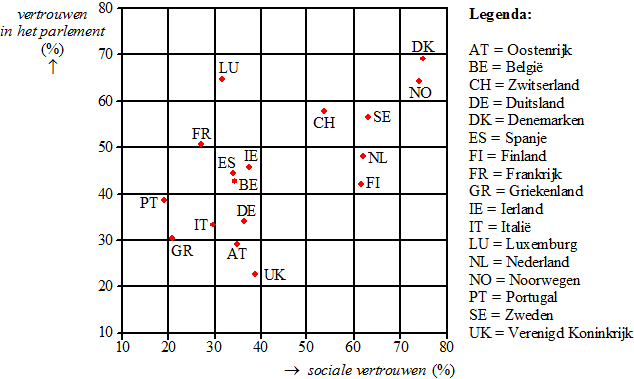
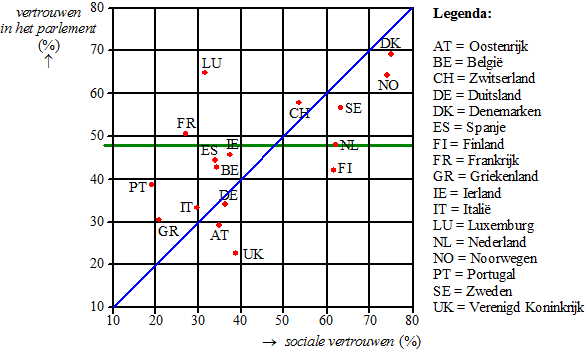
1.	Zie de figuur hiernaast. Er liggen 6 landen boven de groene lijn die het vertrouwen in het parlement in Nederland weergeeft (FR, LU, CH, SE, NO, DK) 6 van de overige 16 is ⁶/₁₆ • 100% = 37,5%

2.	De landen waar het sociale vertrouwen groter is dan het vertrouwen in het parlement liggen onder de blauwe lijn (daarop is het vertrouwen gelijk) Dat zijn: AT = Oostenrijk UK = Verenigd Koninkrijk DE = Duitsland FI = Finland NL = Nederland SE = Zwden NO = Noorwegen DK = Denmarken

3.	De steekproefproportie was ⁴²⁹²/₇₄₀₀ = 0,58 De standaarddeviatie is dan √(^{0,58 • 0,42}/₇₄₀₀) = 0,0057 p + 2σ = 0,5914 ofwel 59,1% p - 2σ = 0,5696 ofwel 57,0% Dit interval ligt binnen het in de opgave gegeven interval, dus uitspraak 1 klopt.

4.	5 = 1 + ^d/₁₀ ^d/₁₀ = 4 d = 40 Een recreatieve duiker kan maximaal 40 meter diep duiken.

5.	De hoeveelheid in de fles is 12 • 200 = 2400 d = 19 geeft p = 1 + 19/10 = 2,9 De benodigde hoeveelheid is dan L = 20 • 2,9 • 45 = 2610 Hij kan de duik dus NIET maken.

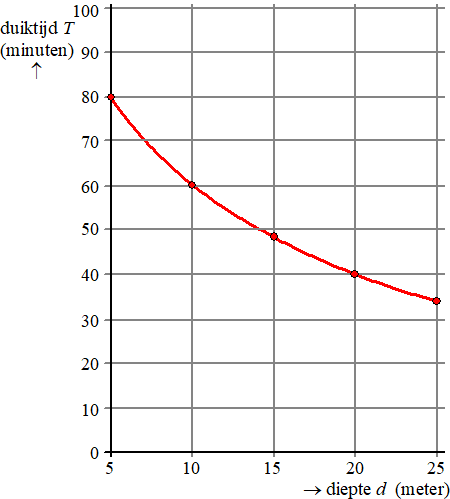
6.	Kies vijf combinaties van d en p Bijvoorbeeld: d = 5 en p = 1,5 geeft 20 • 1,5 • T = 2400 dus T = 80 d = 10 en p = 2 geeft 20 • 2 • T = 2400 dus T = 50 d = 15 en p = 2,5 geeft 20 • 2,5 • T = 2400 dus T = 48 d = 20 en p = 3 geeft 20 • 3 • T = 2400 dus T = 40 d = 25 en p = 3,5 geeft 20 • 3,5 • T = 2400 dus T = 34 Dat geeft de volgende punten en grafiek:



7.	43% van 1212195 is 521244 het totaal was 2575308 dus dat is ⁵²¹²⁴⁴/_2575308 • 100% = 20,2%

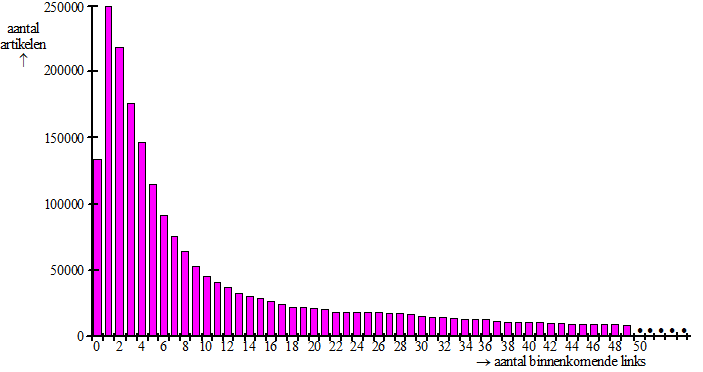
8.	de modus is de hoogste staaf en die is 1 de verdeling is rechtsscheef (staart aan de rechterkant) dus het gemiddelde is groter dan de mediaan (een staafje aan de rechterkant verder naar rechts verplaatsen vergroot het gemiddelde en laat de mediaan gelijk). Er waren ongeveer 2600000 metingen dus de mediaan is nummer 1300000 en die zit rechts van de modus (bij de eerste twee staven heb je minder dan 1300000) De volgorde is dus modus - mediaan - gemiddelde.

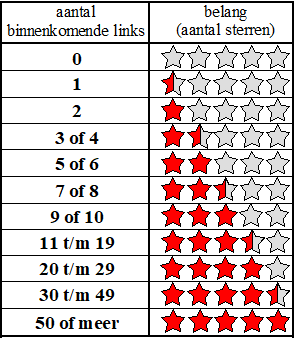
9.	tm 1,5 sterren zijn de groepen met 0, 1, 2, 3 binnenkomende links. 133515 (klasse 0) + 465915 (klassen 1 + 2) = 599430 een kwart van 2575308 is 643827 klasse 3 heeft ongeveer frequentie 175000 en passeert dus de 25%. Dus het eerste kwartiel ligt in klasse 3, en dat is die met 1,5 sterren.

10.	boxplot: de helft heeft 9 of minder binnenkomende links staafdiagram: de modus is 1.

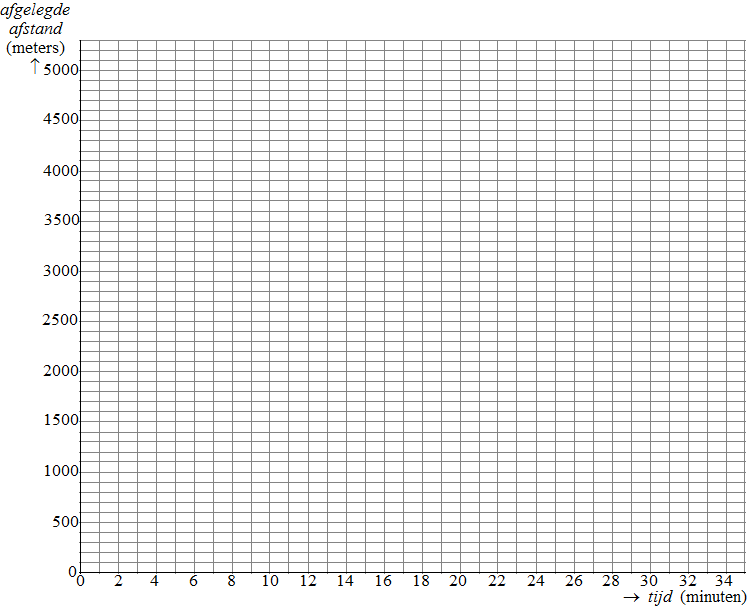
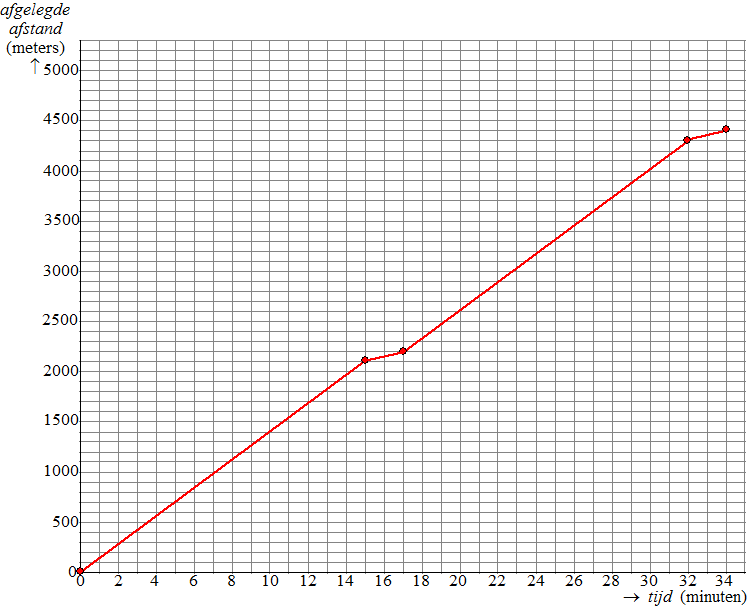
11.	15 minuten hardlopen geeft 15 • 140 = 2100 meter, dus de grafiek gaat door (0, 0) en (15, 2100) 2 minuten wandelen geeft 2 • 50 = 100 erbij, dus de grafiek gaat door (17, 2200) 15 minuten hardlopen geeft weer 2100 meter erbij, dus de grafiek gaat door (32, 4300) 2 minuten wandelen geeft weer 100 meter erbij dus de grafiek gaat door (34, 4400) Dat geeft deze grafiek:



12.	9 km/uur geeft in 1 minuut ⁹/₆₀ = 0,15 km dus in H minuten 0,15H km de wandelsnelheid is ⁹/_2,5 = 3,6 km/uur dus in 1 minuut ^3,6/₆₀ = 0,06 km dus in W minuten 0,06W km. Samen geeft dat 0,15H + 0,06W en dat is inderdaad de gevraagde formule.

13.	laatste dag van week 10: H = 30 en W = 0 dus A = 0,15 • 30 + 0,06 • 0 = 4,5 km eerste dag van week 1: H = 9 en W = A = 0,15 • 9 + 0,06 • 9 = 1,89 het verschil is 4,5 - 1,89 = 2,61 km en dat is 2610 m.

14.	A = 0,15 • H + 0,06 • W vervang W door (60 - H): A = 0,15 • H + 0,06 • (60 - H) A = 0,15 • H + 3,6 - 0,06 • H A = 0,09 • H + 3,6

15.	begin met 100% , dan is er na 30 jaar nog 50% over. Dus 50 = 100 • g³⁰ g³⁰ = 0,5 g = 0,5^1/30 = 0,9772 Dat is een afname van 2,28% per jaar.

16.	Tien keer halveren betekent vermenigvuldigen met 0,5¹⁰ = 0,0009766 dan is er dus nog 0,09766% over.

17.	2,058^0,1d = (2,058^0,1)^d = 1,075^d D = 1 - (2,058^0,1d)^-1 = 1 - (1,075^-1)^d = 1 - 0,93^d

18.	De 8% moet worden teruggebracht tot 5%, dus het beton mag nog ⁵/₈ deel doorlaten en dat is 62,5% 62,5 = ¹⁰⁰/_(1,021d₎ Y1 = 62.5 en Y2 = 100/(1.021^X) en dan intersect geeft X = d = 23 cm.

19.	Hij moet heen en terug dus dat is per jaar 200 • 2 = 400 passages. standaardtarief: 40 • 5 = 2000 met t-tag: 150 t-tag tarief: 150 • 3,80 = 570 250 veelgebruikerstarief : 250 • 3,05 = 762,50 samen met de t-tag dus 1332,50 Dat scheelt 2000 - 1332,50 = €667,50

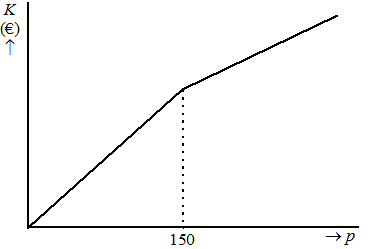
20.	Het eerste deel gaat door (0, 0) en (150, 570) helling ^{(570 - 0)}/_{(150 - 0)} = 3,8 beginwaarde 0 dus de formule is K = 3,8 • p Het tweede deel gaat door (150, 570) en bijvoorbeeld (400, 1332.50) (vraag 13) Helling ^{(1332.50 - 570)}/_{(400 - 150)} = 3,05 (kan natuurlijk ook door in te zien dat dat gewoon het veelgebruikerstarief is) beginwaarde: 570 = 3,05 • 150 + b geeft b = 112,50 De formule is dus K = 0,39 • p + 112,50

21.	Dit is dus 121% Voor de kosten zonder BTW moet je delen door 1,21 ofwel vermenigvuldigen met ¹/_1,21 = 0,8264... Dat geeft K = 0,8264... • (11,15p + 412,5) K = 9,21p + 340,91

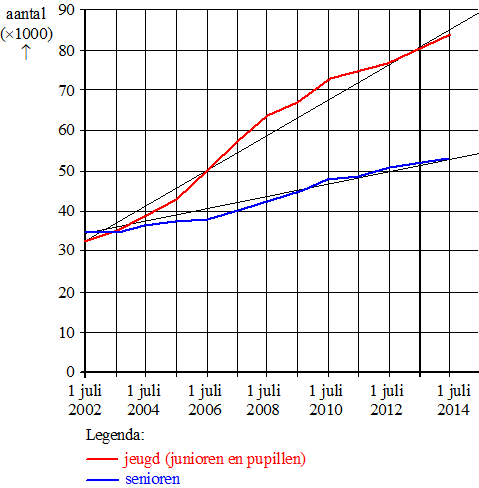
22.	bij de senioren neemt het in twaalf jaar toe van 35000 naar 53000 de helling is ^{(53000 - 35000)}/₁₂ = 1500 en het beginpunt 35000 de lijn daarbij heeft vergelijking S = 1500t + 35000 bij de junioren neemt het in twaalf jaar toe van 33000 naar 85000 de helling is ^{(85000 - 33000)}/₁₂ = 4333 en het beginpunt is 33000 de lijn daarbij heeft vergelijking J = 4333t + 33000 als de senioren 35% zijn, dan geldt: S = 0,35(S + J) 1500t + 35000 = 0,35(1500t + 35000 + 4333t + 33000) 1500t + 35000 = 0,35(5833t + 68000) 1500t + 35000 = 2041,55t + 23800 11200 = 541,55t t = 20,68 dat zal dan zijn in 2002 + 21 = 2023