HAVO WA, 2011 - I

 

Zuinig rijden.
       
Tijdens rijlessen leer je om in de auto bij foto 20 km per uur van de eerste naar de tweede versnelling te schakelen.
Daarna ga je bij 40 km per uur naar de derde versnelling, bij 60 km per uur naar de vierde en ten slotte rond de 90 km per uur naar de vijfde. Iedere versnelling heeft een ideale snelheid.
Maar is dat ook de zuinigste snelheid?
Om dit te onderzoeken heeft men met dezelfde auto steeds met andere snelheden en in een andere versnelling telkens hetzelfde traject afgelegd en daarbij steeds de literafstand L (de afstand die je met 1 liter benzine kunt afleggen) gemeten. Een deel van de resultaten staat in de volgende tabel.

       
Literafstand bij 80 km per uur
versnelling 3 4 5
literafstand  L (km) 16,92 19,63 21,68
       
In deze tabel kun je zien dat je bij 80 km per uur het beste in de vijfde versnelling kunt rijden, omdat je dan 21,68 km kunt afleggen met 1 liter benzine.

Je rijdt op dit traject met een snelheid van 80 km per uur. Je begint met een volle tank van 35 liter benzine en je rijdt die tank helemaal leeg.
       
3p. 1. Bereken hoeveel km je in de vijfde versnelling meer kunt afleggen dan in de vierde versnelling
     

 
In de tabel hier onder staat de literafstand L voor verschillende snelheden in de vijfde versnelling.
       
literafstand in de vijfde versnelling.
snelheid v (km per uur) 40 50 60 70 80 90
literafstand L (km) 29,03 27,19 25,35 23,51 21,68 19,84
       
Je legt in de vijfde versnelling een traject van 300 km af. Als je 80 km per uur rijdt, heb je deze afstand sneller afgelegd dan wanneer je 60 km per uur rijdt. Maar je verbruikt wel meer benzine.
       
3p. 2. Bereken hoeveel liter benzine je dan meer verbruikt.
     

 
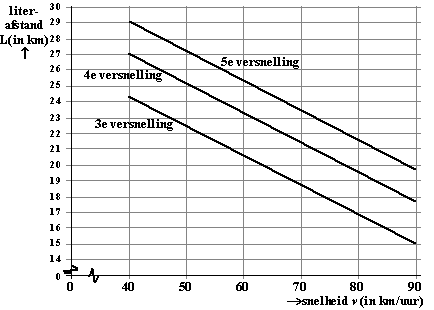
De resultaten van het onderzoek zijn in de figuur grafisch weergegeven.
       

       
In de figuur kun je voor de derde, vierde en de vijfde versnelling bij iedere snelheid de literafstand aflezen. De figuur bestaat uit drie evenwijdige rechte lijnen.

Je rijdt 70 km per uur in de vierde versnelling.
       
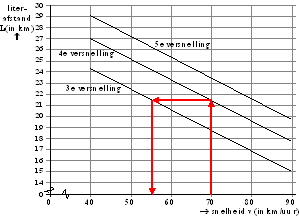
3p. 3. Bepaal met behulp van de figuur met welke snelheid je in de derde versnelling kunt rijden bij dezelfde literafstand. Licht je werkwijze toe.
     

 
Voor de vierde en de vijfde versnelling worden deze lineaire verbanden beschreven door de formules:
       Lvierde versnelling = −0,1838 • v + 34,33
       Lvijfde versnelling = −0,1838 • v + 36,38
Hierin is L de literafstand in km en v de snelheid in km per uur.
De formule voor de literafstand in de derde versnelling Lderde versnelling ontbreekt in het bovenstaande.
       
4p. 4. Stel op basis van bovenstaande gegevens deze formule op.
     

 
Als je wilt weten met welke snelheid je mag rijden in de vijfde versnelling om een bepaalde literafstand te halen, is het handig het gegeven verband tussen de literafstand en de snelheid te schrijven in de vorm:  v = a • Lvijfde versnelling + b
       
4p. 5. Leid uit het gegeven verband tussen Lvijfde versnelling en v een formule van bovenstaande vorm af. Rond a en b af op ้้n decimaal.
     

 
       
De grootste taart.
       
Omdat je winnaar van een wedstrijd bent, krijg je ้้n voor ้้n in willekeurige volgorde een aantal taarten van verschillende grootte te zien. Je weet van tevoren hoeveel taarten er getoond zullen worden, maar je hebt geen idee hoe
groot de taarten zijn.
Direct na elke taart moet je zeggen of je deze wilt of niet, maar je mag maar ้้n keer ja zeggen. Het gaat erom dat je de grootste van alle taarten probeert te kiezen.
De vraag is: wat is de beste strategie om de grootste taart te bemachtigen?
       

       
Vijf taarten
We bekijken een situatie waarin vijf taarten getoond worden. De kleinste taart noemen we 1, de op ้้n na kleinste 2, daarna volgen de taarten 3 en 4 en de grootste taart is taart 5. In het voorbeeld op de afbeelding worden de taarten in de volgorde 4, 2, 3, 5, 1 getoond. De taarten worden echter, zoals al gezegd, in willekeurige volgorde gepresenteerd.
       
3p. 6. Bereken de kans dat de taarten in de volgorde 1, 2, 3, 4, 5 te zien zijn.  
     

 
We bekijken enkele strategie๋n om te proberen de grootste taart te bemachtigen. Daartoe nemen we de wat eenvoudiger situatie waarbij in totaal maar vier taarten getoond worden. De kleinste taart is ook nu taart 1, daarna volgen de taarten 2 en 3 en taart 4 is in dit geval de grootste taart.

Strategie van Richard bij vier taarten
Richard denkt dat het een willekeurige gok is en hij besluit om ja te zeggen tegen de tweede taart die hij te zien krijgt.
       
3p. 7. Hoe groot is de kans dat Richard de grootste taart bemachtigt? Licht je antwoord toe.
       
Strategie van Remco bij vier taarten
Remco besluit om de eerste taart die hij te zien krijgt nooit te nemen, maar de eerstvolgende taart die groter is dan die eerste. Hij kiest uiteindelijk wel altijd een taart. Zijn alle volgende taarten kleiner dan de eerste taart, dan kiest hij dus noodzakelijkerwijs de laatste taart.
Remco schrijft alle mogelijke volgordes op. In de tabel wordt steeds de gekozen taart omcirkeld.
       
1k34 1k43 1l24 1l42 1m23 1m32
21l4 21m3 2l14 2l41 2m13 2m31
312m 31m2 321m 32m1 3m12 3m21
412l 413k 421l 423 431k 432
       
3p. 8. Toon met behulp van de tabel aan dat de kans dat hij de grootste taart bemachtigt ongeveer gelijk is aan 0,4583.
     

 
Strategie van Marlies bij vier taarten
Marlies besluit om de eerste twee taarten die ze te zien krijgt nooit te nemen; ze neemt de eerstvolgende taart die groter is dan zowel de eerste als de tweede taart. Zijn alle volgende taarten kleiner dan de eerste twee taarten, dan kiest ze de laatste taart.
       
5p. 9. Onderzoek of Marlies met deze strategie een grotere kans heeft dan Remco op het bemachtigen van de grootste taart. Je kunt hierbij gebruikmaken van de tabel.
     

 
Vijf taarten
Bij vijf taarten blijkt de strategie van Marlies de gunstigste te zijn. De kans dat je met deze strategie de grootste kiest, is gelijk aan  52/120
Een klas van 26 leerlingen doet een experiment: alle leerlingen gaan proberen om met de strategie van Marlies uit vijf taarten de grootste te kiezen.
       
4p. 10. Bereken de kans dat minstens 10 leerlingen de grootste taart kiezen.
     

 
 
Woei wordt waaide
       
We noemen werkwoorden regelmatig wanneer ze worden vervoegd als het werkwoord fietsen: fietsen — fietste — gefietst, of als het werkwoord huilen: huilen — huilde — gehuild. Er is een vaste uitgang voor de verleden tijd en het
voltooid deelwoord. Wanneer een werkwoord bij de vervoeging verandering van klinkers (a, e, i, …) of medeklinkers (b, c, d, …) vertoont, spreken we van een onregelmatig werkwoord. Een voorbeeld hiervan is het werkwoord lopen, dat wordt vervoegd als lopen — liep — gelopen.
Veel werkwoorden die tegenwoordig regelmatig zijn, waren vroeger onregelmatig. Onregelmatige werkwoorden hebben namelijk de neiging in de loop der tijd regelmatig te worden. Denk maar aan het werkwoord waaien.
Sommige oudere mensen zeggen nog: ‘Gisteren woei het erg!’, terwijl vooral jongeren zeggen: ‘Gisteren waaide het erg!’

Wetenschappers hebben dit verschijnsel onderzocht voor Engelse werkwoorden. Zij turfden het aantal onregelmatige werkwoorden in drie verschillende perioden. Je begrijpt dat in het onderzoek alleen die werkwoorden betrokken zijn waarvan uit elke periode gegevens bekend waren.
Van de 177 onregelmatige werkwoorden in het Oudengels (800 na Christus) waren er in het Middelengels (1200 na Christus) 145 nog steeds onregelmatig, en in het moderne Engels (2000 na Christus) nog maar 98.

Er geldt bij benadering dat het aantal Engelse onregelmatige werkwoorden daalt volgens een exponentieel verband.
       
5p. 11. Bereken met behulp van de bovenstaande gegevens het afnamepercentage per 100 jaar.
     

 
In werkelijkheid zijn er natuurlijk meer onregelmatige werkwoorden dan alleen die werkwoorden van het onderzoek. We nemen aan dat bij benadering het volgende verband tussen het totaal aantal Engelse onregelmatige werkwoorden W en het jaartal t geldt:   W = 432 • 0,9995t 
       
3p. 12. Bereken met behulp van dit verband in welk jaar het aantal Engelse onregelmatige werkwoorden nog maar 80 zal zijn.
     

 
In het moderne Engels (2000 na Christus, dus t = 2000) is slechts 3% van de werkwoorden onregelmatig.
       
4p. 13. Bereken met behulp van het verband het totaal aantal Engelse werkwoorden in het jaar 2000.
     

 
Het regelmatig worden van werkwoorden gebeurt sneller naarmate de woorden minder vaak worden gebruikt.
De wetenschappers hebben alle onderzochte onregelmatige werkwoorden in zes groepen ingedeeld. De meest gebruikte, to be en to have, zitten in groep 1 en de minst gebruikte zitten in groep 6.

In groep 3 blijkt het aantal werkwoorden in de periode 800 tot 2000 na Christus afgenomen te zijn van 37 tot 33. In deze groep 3 zijn de werkwoorden to help, to reach, to walk en to work regelmatig geworden. Ga ervan uit dat binnen deze groep het aantal werkwoorden bij benadering exponentieel afneemt met 0,01% per jaar.
       
4p. 14. Bereken hoeveel jaar het duurt tot het aantal werkwoorden in groep 3 gehalveerd is.
     

 
De onderzoekers onderzochten dit voor elke groep en leidden hieruit de volgende vuistregel af: wordt een onregelmatig werkwoord n keer zo vaak gebruikt, dan duurt het n keer zo lang totdat dit werkwoord regelmatig wordt. Een onregelmatig werkwoord dat bijvoorbeeld 100 keer zo vaak gebruikt wordt als een ander onregelmatig werkwoord, zal er √100 = 10 keer zo lang over doen om regelmatig te worden.

In Nederland heeft men uit stukken tekst van in totaal 100 miljoen woorden de 10 meest gebruikte Nederlandse werkwoorden gehaald. Zie de tabel. Het valt vrijwel direct op dat de eerste 9 onregelmatig zijn.
       
  werkwoord frequentie
1 zijn 2264398
2 worden 946623
3 hebben 872661
4 kunnen 569152
5 zullen 382900
6 moeten 345098
7 gaan 285026
8 komen 267532
9 zeggen 230606
10 maken 214280
       
Neem aan dat het Nederlandse werkwoord komen pas na 13 000 jaar regelmatig wordt, zoals men dat ook verwacht voor het Engelse werkwoord to come. Neem verder aan dat de vuistregel ook geldt voor de Nederlandse onregelmatige werkwoorden. Dan kun je met behulp van de tabel berekenen hoeveel jaar het duurt voor het werkwoord worden regelmatig wordt.
       
3p. 15. Bereken met behulp van de frequenties in de tabel hoeveel jaar het duurt voor het werkwoord worden regelmatig wordt.
     

 
       
Zijn meisjes beter in taal?
       
Vaak wordt beweerd dat meisjes beter in taal zijn dan jongens. Maar hoe kun je dat onderzoeken? Een bekende methode is om na een toets het gemiddelde van de jongens te vergelijken met dat van de meisjes. Maar er zijn ook andere methoden. In deze opgave bekijken we een manier van vergelijken die is opgesteld door Frank Wilcoxon. Hij kijkt vooral naar de rangschikking van de jongens en de meisjes.

Vier meisjes en drie jongens
Bij een taaltoets die door vier meisjes en drie jongens wordt gemaakt, zijn maximaal 250 punten te behalen. De meisjes halen de scores 162, 217, 231 en 240 en de jongens halen de scores 119, 145 en 179. Je kunt nu deze scores rangschikken van laag naar hoog en daarbij noteren of het om een jongen (J) of een meisje (M) gaat. Er ontstaat zo een rij met driemaal een J en viermaal een M. In dit geval krijg je de rij J J M J M M M.
       
3p. 16. Bereken hoeveel verschillende rijen er mogelijk zijn met driemaal een J en viermaal een M.
     

 
Van elke rij kunnen we de zogenoemde U-waarde berekenen. Dit gaat als volgt: tel voor elke M het aantal J’tjes dat erv๓๓r staat en tel daarna alle uitkomsten bij elkaar op.
De U-waarde van het rijtje J J M J M M M is dus 2 + 3 + 3 + 3 = 11. Deze U-waarde is hoog want op ้้n na scoren alle meisjes hoger dan alle jongens.

De U-waarde geeft aan in hoeverre de scores van jongens en meisjes verschillen. Dat betekent:
− U-waarde hoog: de meisjes scoren hoog en de jongens laag;
− U-waarde laag: de jongens scoren hoog en de meisjes laag;
− U-waarde middelmatig: er is weinig verschil tussen meisjes en jongens.
       
3p. 17. Geef een voorbeeld van een rij bestaande uit driemaal een J en viermaal een M met U-waarde 5.
       
Door bij alle mogelijke rijen de U-waarde te bepalen kun je de kansverdeling van U opstellen. Daarbij ga je er dus van uit dat alle rangschikkingen even waarschijnlijk zijn. Deze kansverdeling is weergegeven in de figuur.
       

       
Bij grotere groepen gaat dit kanshistogram op de grafiek van een normale verdeling lijken. De U-waarde is dan bij benadering normaal verdeeld met:
   
  gemiddelde = 0,5• nm • nj
 

Hierin is nm het aantal meisjes en nj het aantal jongens.

Een havo 5-groep met 70 meisjes en 75 jongens maakt de taaltoets. De U-waarde die je mag verwachten als jongens en meisjes ongeveer even goed scoren, zal rond het gemiddelde liggen.
       
4p. 18. Bereken de kans dat de U-waarde tussen 2400 en 2800 ligt, uitgaande van de hierboven genoemde formules.
     

 
Als de U-waarde van een groep niet in de buurt van het gemiddelde ligt maar veel hoger is, kun je zeggen dat de meisjes in die groep beter in taal zijn dan de jongens in die groep. Maar wat is precies ‘veel hoger’? Wilcoxon trekt de grens als volgt: als de U-waarde bij de hoogste 5% zit, uitgaande van bovenstaande normale verdeling, dan wordt besloten dat de meisjes beter in taal zijn dan de jongens.

Na verwerking van de scores van genoemde havo 5-groep blijkt de U-waarde gelijk te zijn aan 2984.
       
4p. 19. Onderzoek of voor deze havo 5-groep besloten wordt dat de meisjes beter in taal zijn dan de jongens.
     

 
       
       
Gebruiksduur.
       
Een fabriek produceert een bepaald type huishoudelijk apparaat dat door veel consumenten wordt gekocht. Sommige van die apparaten gaan lang mee, andere zijn al vrij snel defect.
De serviceafdeling van de fabriek verzamelt informatie over de gebruiksduur van dit type. Dat doet men door te onderzoeken op welk moment de apparaten defect raken.
Er zijn twee verschillende formules waarmee men de gebruiksduur probeert te beschrijven:
   
  formule 1:   P =100 • (1− 0,8t )
formule 2:   P =100 − (50t +100) • 0,61t
       
Hierin is P het percentage apparaten dat na t jaar of eerder defect is geraakt.
       
3p. 20. Bij welke van de twee formules is na 5,5 jaar ruim driekwart van de apparaten defect? Licht je antwoord toe.
     

 
Op tijdstip t = 0 geven beide formules hetzelfde percentage, namelijk 0. Er is echter nog een ander tijdstip waarop beide formules hetzelfde percentage opleveren.
       
3p. 21. Bereken voor welke andere waarde van t beide formules hetzelfde percentage geven. Rond je antwoord af op ้้n decimaal.
     

 
Formules die gebruikt kunnen worden om de gebruiksduur te beschrijven, moeten aan de volgende drie eisen voldoen:
1 op t = 0 moet gelden dat P = 0 ;
2 als t groter wordt, moet P toenemen;
3 als t heel groot wordt, moet P naderen naar 100.
       
3p. 22. Leg uit hoe je aan formule 1 kunt zien dat deze aan de tweede eis voldoet.
     

 
Met formule 1 kun je het percentage apparaten berekenen dat binnen een bepaald aantal jaren defect raakt. Op basis van dat percentage kan een aanname over de kans op defect raken worden gedaan. Zo volgt bijvoorbeeld uit formule 1 dat 20% van de apparaten binnen een jaar defect raakt. We nemen dan aan dat de kans dat een apparaat binnen een jaar defect raakt, gelijk is aan 0,20. In de volgende vraag gaat het om defect raken binnen vijf jaar.

Een winkel heeft op een dag 11 van deze apparaten verkocht. De gebruiksduur ervan wordt beschreven met formule 1. De apparaten raken onafhankelijk van elkaar op een bepaald tijdstip defect.
       
5p. 23. Bereken de kans dat hoogstens 6 van deze apparaten binnen 5 jaar defect raken.
     

 

 

UITWERKING
   
Het offici๋le (maar soms beknoptere) correctievoorschrift kun je HIER vinden. Vooral handig voor de onderverdeling van de punten.
   
1. in de vierde versnelling rij je met 35 liter 35 • 19,63 = 690 km
in de vijfde versnelling rij je met 35 liter 35 • 21,68 = 760 km
Dus in de vierde versnelling rij je 70 km meer.
   
2. maak verhoudingstabellen:
 
bij 80 km/uur
liter 1 ??
km 21,68 300
bij 60 km/uur
liter 1 ??
km 25,35 300
   
  Bij 80 km/uur geeft dat  1 • 300/21,68 = 13,8 liter
Bij 60 km/uur geeft dat  1 • 300/25,35 = 11,8 liter
Dus je verbruikt 2 liter minder.
   
3. zie de figuur hiernaast.
ga bij 70 km/uur verticaal omhoog naar de lijn van de 4e versnelling.
Dat geeft de literafstand (ongeveer 21,5).
Ga daarna horizontaal opzij naar de lijn van de 3e versnelling (blijf dus bij dezelfde literafstand)
Ga dan verticaal omlaag om te kijken welke snelheid daarbij hoort.
Het is ongeveer 55 km/uur
 

   
4. Als de lijnen evenwijdig zijn, dan zal de formule er uitzien als  L = -0,1838 • v + b
(immers dezelfde lijnen hebben hetzelfde hellinggetal)
Vul een punt van de grafiek in, bijvoorbeeld (90, 15)
15 = -0,1838 • 90 + b  ⇒  15 = -16,542 + b  ⇒  b = 31,542
De formule is  L = -0,1838 • v + 31,542
   
5. L =  -0,1838 • v + 36,38
L - 36,38 = -0,1838 • v
L/-0,1838  - 36,38/-0,1838 = v
L • 1/-0,1838 + 197,9 = v
-5,4L + 197,9 = v
   
6. voor de eerste taart zijn 5 mogelijkheden
voor de tweede taart daarna nog 4 mogelijkheden, dan voor de derde taart nog 3, enz.
In totaal zijn er 5 • 4 • 3 • 2 • 1 = 120 mogelijkheden
de kans op precies deze ene volgorde is daarom 1/120.
   
7. elke taart heeft dezelfde kans om de tweede te zijn, dus 1/4.
   
8. Kijk naar de tabel.
Hij kiest de grootste taart bij 11 van de 24 mogelijkheden.
De kans is daarom 11/24.
   
9. Net zo'n tabel maken geeft dit:
 
12(3)4 12(4)3 132(4) 13(4)2 142(3) 143(2)
21(3)4 21(4)3 231(4) 23(4)1 241(3) 243(1)
312(4) 31(4)2 321(4) 32(4)1 341(2) 342(1)
412(3) 413(2) 421(3) 423(1) 431(2) 432(1)
  Er zijn 10 gevallen waarin ze de grootste taart kiest, en dat is minder dan de 11 van Remco.
De kans van Marlies is dus NIET groter.
   
10. Dit is binomiaal verdeeld met n = 26 en p = 52/120.
P(minstens 10) = 1 - P(kleiner of gelijk aan 9) = 1 - binomcdf(26, 52/120, 9) = 0,76
   
11. het gaat van 177 in jaar 800 naar 98 in jaar 2000
Dat is een factor  98/177 in 1200 jaar.
Per jaar is de groeifactor dan (98/177)1/12 = 0,95
Dat is een afname van 100 - 95 = 5%
   
12. 80 = 432 • 0,9995t
Y1 = 80
Y2 = 432 • 0,9995^X
intersect geeft t = 3372
   
13. t = 2000 geeft  W = 432 • 0,99952000 = 159
159 is dus 3%, dan is 1% gelijk aan 159/3
100% is dan gelijk aan 100 • 159/3 = 5300
   
14. een afname van 0,01% betekent een groeifactor van 1 - 0,0001 = 0,9999
als de beginhoeveelheid bijvoorbeeld 100 is, dan is de eindhoeveelheid (halveren) gelijk aan 50.
50 = 100 • 0,999t
Y1 = 50
Y2 = 100 • 0,999^X
intersect geeft t = 6900
   
15. worden wordt  946623/267532 = 3,54 keer zo vaak gebruikt als komen.
het duurt dan √3,54 keer zo lang.
Dat is dan 13000•√3,54 = 24000 jaar.
   
16. 7 nCr 3 = 35 rijen.
   
17. 5 is bijvoorbeeld  1 + 1 + 1 + 2
Dat is het rijtje  JMMMJMJ
   
  een andere mogelijkheid is 0 + 1 + 2 + 2  met rijtje  MJMJMMJ
  of 0 + 0 + 2 + 3  met rijtje  MMJJMJM
   
18. nm = 70 en nj = 75
dan is  gemiddelde = 0,5 • 70 • 75 = 2625
standaarddeviatie = √(70 • 75 • 146/12) = √63875 = 252,7
tussen de 2400 en 2800 is  normalcdf(2400, 2800, 2625, 252,7) = 0,57
   
19. gemiddelde is 2625 en standaarddeviatie is 252,7 (zie vorige vraag)
groter dan 2984 is kans  normalcdf(2984, 10000..., 2625, 252.7) = 0,08
dat is ongeveer 0,08
dat is nog niet kleiner dan 0,05 dus er kan NIET worden besloten dat meisjes beter in taal zijn dan jongens.
   
20. t = 5,5 in beide formules invullen:
P1 = 100 • (1 - 0,85,5 ) = 100 • (1 - 0,293) = 100 • 0,707 = 70,7%
P2 = 100 - (50 • 5,5 + 100) • 0,615,5 = 100 - 375•0,066 = 100 - 0,247 = 75,3%
Dus dat is zo bij formule 2.
   
21. Y1 = 100 • (1 - 0,8^X)
Y2 = 100 - (50X + 100)•0,61^X
intersect levert t =  4,1 jaar.
   
22. als t groter wordt, dan wordt 0,8t kleiner  (want 0,8 < 1)
als 0,8t kleiner wordt dan wordt 1 - 0,8t groter
dan wordt 100 • (1 - 0,8t) ook groter.
Dus als t groter wordt, dan wordt P ook groter.
   
23. t = 5  geeft  P = 100  (1 - 0,85) = 100 • 0,67232 = 67,232
elk van de 11 apparaten heeft dus kans 0,67232 om binnen 5 jaar defect te raken.
het aantal defecte apparaten is dan binomiaal verdeeld met n = 11 en p = 0,67232
De kans op hoogstens 6 is dan binomcdf(11, 0.67232, 6) = 0,275