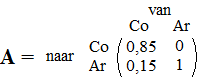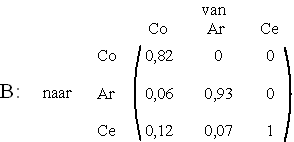HAVO WA, 2000 - I

 

OPGAVE 1.  Seychellenzangers.
       
Seychellenzangers zijn kleine vogeltjes die nauwelijks kunnen vliegen. Rond 1968 kwamen ze alleen nog voor op het eilandje Cousin in de Indische Oceaan.Hun aantal was zo klein dat de soort dreigde uit te sterven. In 1968 werd Cousin een natuurreservaat. Daardoor nam het aantal Seychellenzangers weer snel toe. In 1968 waren er 26 Seychellenzangers en in 1976 waren er alweer 250.

Stel dat deze populatie Seychellenzangers in de periode van 1968 tot 1976 exponentieel groeide.
       
4p.

1.

 Toon aan dat het aantal Seychellenzangers dan per jaar met ongeveer 33% groeide.
       
In 1983 waren er ongeveer 320 Seychellenzangers en dat aantal bleef de jaren daarna gelijk. Het feit dat ze alleen maar voorkwamen op Cousin,maakte het voortbestaan van deze soort toch riskant. Daarom wilde men een aantal vogeltjes overbrengen naar Aride,een eilandje in de buurt van Cousin. Om niet te veel onrust te veroorzaken onder de vogeltjes,bracht men kort na elkaar twee keer een klein aantal Seychellenzangers over van Cousin naar Aride. Daarbij bleven alle vogeltjes in leven, zodat het totale aantal 320 bleef. Per keer werd een vast percentage van de op dat moment op Cousin aanwezige vogeltjes naar Aride gebracht.

In matrix A staan de getallen die horen bij één keer overbrengen:
       

       
6p.

2.

 Bereken het totaal aantal Seychellenzangers op Aride na twee keer overbrengen.
       
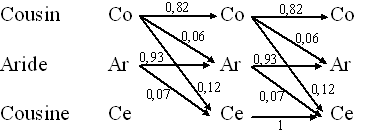
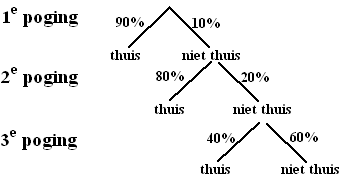
Begin jaren negentig was het aantal Seychellenzangers op Cousin weer aangegroeid tot 320. Opnieuw wilde men Seychellenzangers overbrengen. Nu niet alleen van Cousin naar Aride, maar ook van Cousin naar een derde eilandje, Cousine. Ook bracht men Seychellenzangers van Aride naar Cousine. Net als in 1983 gebeurde dit in twee keer, kort na elkaar. In onderstaand schema is dit overbrengen weergegeven.

De getallen bij de pijlen staan voor het deel van de populatie dat per keer overgebracht werd.
       

       
De getallen die horen bij één keer overbrengen, staan ook in matrix B:
       

       
Het twee keer na elkaar overbrengen kan met één matrix N worden beschreven.
       
6p.

3.

 Stel deze matrix N op. Je mag daarbij uitgaan van het schema of van matrix B.
       
OPGAVE 2.  Hoe lang is een Nederlander?
In een krantenartikel werd beschreven hoe een kind zijn (of haar) toekomstige lichaamslengte kan berekenen:

"Tel de lengten (in cm) van je vader en je moeder bij elkaar op en deel het getal door twee. Je hebt dan de gemiddelde lengte van je ouders. Als je een meisje bent, trek je daar zes van af. Als je een jongen bent, tel je er zes bij op. Dat doe je omdat mannen gemiddeld langer worden dan vrouwen. Daarna tel je er nog eens drie bij op. Dat moeten zowel de jongens als de meisjes doen, want die drie centimeter worden alle kinderen gemiddeld langer dan hun ouders. Dan weet je hoe lang je waarschijnlijk zult zijn als je stopt met groeien".
4p

4.

 Bereken de te verwachten lengte van een jongen met een vader van 185 cm en een moeder die 167 cm lang is.
 

 
Het is mogelijk om met behulp van bovenstaande tekst formules te maken om iemands te verwachten lengte in cm te bepalen. Noem de lengte en cm van de vader va en die van de moeder mo.
4p

5.

 Stel een formule op voor de te verwachten lengte van een meisje.
 

 

In het krantenartikel stond ook:
"Elke generatie wordt 3 cm langer dan de vorige. Dat betekent dat de gemiddelde lengte van de Nederlanders elke 10 jaar 1 cm groter wordt. Als dat zo doorgaat, dan is in het jaar 2150 de helft van de Nederlandse mannen meer dan 2,00 meter".
Neem aan dat de stijging van de gemiddelde lengte inderdaad zo verloopt als in de tweede tekst staat. Je mag er van uitgaan dat de lengte van de Nederlandse mannen normaal verdeeld is met een constante standaardafwijking van 8 cm, maar met een stijgend gemiddelde.
7p

6.

 Hoeveel procent van de Nederlandse mannen is dan in het jaar 2010 langer dan 2,00 meter?
Licht je antwoord toe.
   
In het jongerentijdschrift Pauze stond een aantal jaren geleden een andere methode om je toekomstige lengte te berekenen. Die methode kan met de volgende formules worden beschreven:

lengte jongen = 2/3  • va + 1/3 • mo + 7   en   lengte meisje = 2/3 • va + 1/3 • mo – 1,

waarbij va en mo de lengte in cm van de vader, respectievelijk de moeder zijn.
Een jongen en een meisje blijken volgens deze methode even lang te worden. Hun vaders zijn precies even lang.
 
     
5p.

7.

 Bereken hoe groot het lengteverschil van hun moeders is.
 

 

 

OPGAVE 3.  Luchtdrukte.
In deze opgave bekijken we de aankomst van vliegtuigen op een vliegveld. Gewoonlijk zeggen we bijvoorbeeld dat er gemiddeld 10 vliegtuigen per uur aankomen. Het is dan meestal niet zo dat er elke zes minuten een vliegtuig aankomt. Soms komen er veel, dan weer weinig vliegtuigen achter elkaar binnen. De tussentijd van een vliegtuig is de tijd (in minuten) tussen de aankomst van het vorige vliegtuig en de aankomst van het betreffende vliegtuig. Het eerste vliegtuig dat aankomt nadat het vliegveld geopend is,  heeft geen tussentijd. In de figuur hieronder zie je de aankomsttijden van de eerste vijf vliegtuigen op een dag en de bijbehorende tussentijden.

Alle tussentijden worden vervolgens van groot naar klein op volgorde gezet en in een grafiek weergegeven

In de volgende figuur staan de tussentijden van de vliegtuigen voor een bepaalde periode voor een klein  vliegveld.

In de figuur zijn de 40 tussentijden weergegeven door 40 stippen. Bij elke stip kun je de bijbehorende tussentijd aflezen op de horizontale as en het nummer op de verticale as. Punt Q bijvoorbeeld hoort bij een vliegtuig met tussentijd 68 minuten. Het is tussentijdnummer 5 omdat vier tussentijden nog groter waren. Anders gezegd: er zijn  5 vliegtuigen met een tussentijd van 68 minuten of meer.
Bij punt R hoort de kleinste tussentijd: 1 minuut.
5p

8.

 Teken in onderstaande figuur een histogram van de tussentijden. Geef daarin de frequentie van de tussentijden per klasse weer met een klassenbreedte van 20 minuten.

Als de tussentijden van aankomende vliegtuigen op andere vliegvelden of gedurende andere periodes op de manier van de grafiek boven vraag 8 worden weergegeven, ontstaat telkens een zelfde soort grafiek. In de figuur hieronder is een model van dit type grafiek getekend. Langs de verticale as staan nu percentages.

Je kunt in deze figuur bijvoorbeeld aflezen dat 13% van de vliegtuigen een tussentijd heeft van 50 minuten of meer (punt A) en dat 2,5% een tussentijd heeft van 90 minuten of meer (punt B).

In de figuur lees je ook af dat 50% van de vliegtuigen volgens dit mode een tussentijd heeft van 17 minuten of meer (en ook 50% een tussentijd van minder dan 17 minuten). De gemiddelde tussentijd is niet gelijk aan 17 minuten.

3p

9.

 Onderzoek of de gemiddelde tussentijd groter of kleiner dan 17 minuten is.

Aan de hand van de figuur kan een boxplot van de tussentijden gemaakt worden.
5p

10.

 Teken de boxplot. Licht je werkwijze toe. Gebruik daarbij de figuur hierboven.

Er is een formule van de vorm y = b • gt  die goed past bij de grafiek hierboven.
Hierbij is t de tussentijd in minuten en y het percentage vliegtuigen met een tussentijd van t minuten of meer.
4p

11.

 Hoe groot zijn b en g?  Licht je antwoord toe.

 

OPGAVE 4.  Wiskunde in bad.
Misschien is het je na het nemen van een bad wel eens opgevallen dat het water in het begin sneller wegloopt dan aan het eind.Dit verschijnsel is onderzocht bij verschillende baden. Elk bad had de vorm van een rechthoekige bak. Zie de figuur hier onder.Vanaf het moment dat de stop eruit getrokken werd,is op verschillende tijdstippen de hoogte van het badwater gemeten.Op het tijdstip t = 0 begint het leeglopen en als het bad helemaal leeg is, is de waterhoogte uiteraard 0 geworden.

Voor bad 1 staan de resultaten in de volgende tabel:
     
tijd  t (sec) 0 40 80 120 160
waterhoogte (cm) 48,0 26,7 12,0 3,0 0,0
3p

12.

 Onderzoek of voor bad 1 geldt dat het water steeds langzamer wegloopt naarmate de waterhoogte in het bad verder daalt.
     
Voor een ander bad, bad 2, zijn de meetresultaten in een grafiek weergegeven. Zie onderstaande figuur. In de figuur is te zien dat dit bad na 187 seconden leeggelopen is.
     

     
Bij elk bad kun je de zogenaamde leegloopverhouding berekenen. De leegloopverhouding wordt berekend met de volgende formule:
     

     
Hierbij is de leeglooptijd eerste helft de tijd die nodig is om de waterhoogte van het bad te halveren,uitgaande van de beginsituatie. De leeglooptijd tweede helft is de tijd die nodig is om het bad vervolgens helemaal leeg te laten lopen.
     
6p.

13.

 Bereken met behulp van de figuur de leegloopverhouding van bad 2.
     
Voor een derde bad,bad 3,is het leeglopen te beschrijven met de volgende formule:
     

waterhoogte = (7 – 0,03t)2   met t in seconden en waterhoogte in cm.
     
3p.

14.

  Toon aan dat het leeglopen van bad 3 ongeveer 233 seconden duurt.
     
6p.

15.

  Bereken de leegloopverhouding van bad 3.
     
OPGAVE 5.    Enquête
 
Opiniepeilingen worden vaak telefonisch gedaan, maar voor bepaalde soorten enquêtes stuurt een onderzoeksbureau enquêteurs met een vragenlijst op pad. Aselect worden een aantal adressen getrokken. Het onderzoeksbureau laat enquêteurs die adressen bezoeken om de bewoners van die adressen vragen te stellen.

Voor een onderzoek moeten 1400 adressen worden bezocht. Er zijn hiervoor 4 vaste medewerkers beschikbaar en 16 studenten die dit als bijbaantje hebben. Een vaste medewerker krijgt een groter aantal adressen dan een student. Iedere vaste medewerker krijgt evenveel adressen. Ieder van de 16 studenten krijgt ook een gelijk aantal adressen, maar dat zijn er 30 minder dan het aantal dat een vaste medewerker krijgt.

De 1400 adressen kunnen 'precies' verdeeld worden.
5p

16.

 Laat dit zien door te berekenen hoeveel adressen een vaste medewerker en hoeveel adressen een student krijgt.

 

Als er niet 1400 maar 1405 adressen te verdelen zijn, worden eerst de 1400 adressen 'precies' verdeeld. De overblijvende 5 adressen worden dan verloot onder de 20 enquêteurs. Daarbij heeft iedereen dezelfde kans op een extra adres, maar niemand krijgt er meer dan één adres bij.
4p

17.

 Bereken de kans dat deze 5 adressen allemaal bij de 16 studenten terecht komen.
Wanneer de enquêteur op een adres komt waar niemand thuis is, probeert hij het later voor de tweede keer. Als ook bij het tweede bezoek niemand thuis is, doet hij bij dit adres nog een derde poging. Die derde keer is ook de laatste keer, zelfs als er dan weer niemand thuis is. Uit ervaring weet men dat de kans dat iemand thuis is, de eerste keer het grootst is. Bij de tweede poging is de kans wat kleineren bij het derde bezoek zelfs veel kleiner.
Stel dat bij het eerste bezoek bij 90% van de adressen iemand thuis is. Bij de adressen waar men de eerste keer niet thuis was, is 80% bij het tweede bezoek wel thuis. Op de adressen waar een derde poging nodig is, is bij dat derde bezoek 40% thuis. Zie volgende figuur.

4p

18.

 Bereken de kans dat de enquêteur op een adres pas bij het derde bezoek iemand thuis treft.

Het onderzoek wordt gehouden bij 1400 verschillende adressen
6p

19.

 Bereken hoeveel keer in totaal een adres zal worden bezocht voor dit onderzoek.

 

 

 

UITWERKING
   
Het officiële (maar soms beknoptere) correctievoorschrift kun je HIER vinden. Vooral handig voor de onderverdeling van de punten.
   
1.  
   
2.  
   
3.  
   
4.  
   
5.  
   
6.  
   
7.  
   
8.  
   
9.  
   
10.  
   
11.  
   
12.  
   
13.  
   
14.  
   
15.  
   
16.  
   
17.  
   
18.  
   
19.  
   
20.  
   
21.  
   
22.  
   
23.