HAVO WA, 1994 - II

 

OPGAVE 1.  Voedselketen.
       
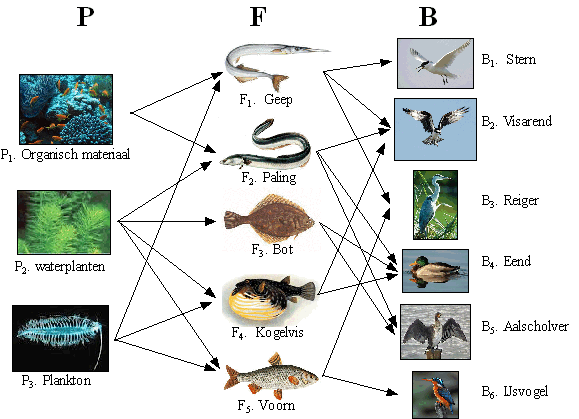
Hieronder zie je een deel van de voedselketen van vogels voor de kust van Long Island (VS). Zo zie je bijvoorbeeld dat een voorn plankton en waterplanten eet. De voorn wordt onder andere door de ijsvogel gegeten.
       

       
Stel dat er sprake is van een verhoging is van de hoeveelheid vergif in de waterplanten. Neem aan dat alleen de aangegeven planten en dieren gegeten worden. Met het voedsel wordt ook het vergif doorgegeven.
       
3p. 1. Mag je een verhoging van de hoeveelheid vergif bij alle genoemde vogels verwachten? Licht je antwoord toe.
       
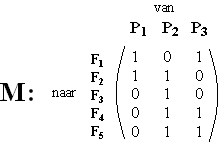
Het is mogelijk bovenstaande voedselketen weer te geven met behulp van matrices. De voedselstromen van P naar F zijn in matrix M weergegeven.

       
Een 1 in de matrix betekent dat de één als voedsel dient voor de ander en een 0 geeft aan dat de één niet door de ander wordt gegeten. Zo betekent bijvoorbeeld het getal 1 linksboven in de matrix dat P1 door F1 wordt gegeten en het cijfer 0 linksonder dat P1 niet door F5 wordt gegeten.
       
5p. 2. Maak een dergelijke matrix N die de voedselstromen van F naar B weergeeft.
       
5p. 3. Vermenigvuldig matrix N met matrix M.
       
3p. 4. Wat is de betekenis van de getallen in de productmatrix van vraag 3?
       
OPGAVE 2.  Glasdikte.
         
in huizen en gebouwen wordt voor grote ruiten dikker glas gebruikt dan voor kleine ruiten. Dat is nodig om de ruit voldoende stevigheid te geven. De benodigde dikte wordt echter niet alleen bepaald door de grootte van de ruit.
Om de minimaal benodigde dikte D van een ruit te bepalen gebruikt men de volgende formule:
D = 0,447 × β × a × q 
In de formule en het vervolg van de opgave worden de volgende symbolen gebruikt:
• D = minimale dikte in mm
• a = kleinste zijde van de ruit in m (zie figuur hieronder)
• b = grootste zijde van de ruit in m.
• β = vormfactor, afhankelijk van b/a  (zie tabel hieronder)
• q = windbelastingsfactor (zie grafiek hieronder)

•

 H = hoogte waar de ruiten in het gebouw zitten in m.
         

         
b/a β
1,00
1,05
1,10
1,15
1,20
1,25
1,30
1,35		 0,535
0,557
0,567
0,595
0,613
0,630
0,645
0,669
b/a β
1,40
1,45
1,50
1,55
1,60
1,65
1,70
1,75		 0,673
0,687
0,699
0,709
0,720
0,729
0,737
0,746
b/a β
1,80
1,85
1,90
1,95
2,00
2,10
2,20
2,30		 0,754
0,762
0,770
0,775
0,780
0,790
0,799
0,806
b/a β
2,40
2,50
3,00
4,00
5,00
groter
dan 5,00
 		 0,811
0,815
0,845
0,860
0,864

0,865
 
         
In een hoog kantoorgebouw hebben alle ruiten dezelfde afmetingen:  a = 2  en b = 3.
         
4p. 5. Laat zien dat de minimale glasdikte voor ruiten op 5 m hoogte ongeveer 14 mm is.
         
5p. 6. Hoeveel procent moeten de ruiten op 60 m hoogte dikker zijn dan de ruiten op 5 m hoogte? Licht je antwoord toe.
         
Stel dat de lengte en de breedte van de ruiten op 100 m hoogte nog mogen variëren. De oppervlakte van de ruit moet wel 6 m2 zijn en de kleinste zijde a moet minstens 1 m zijn.
         
6p. 7. Onderzoek of de minimale dikte het kleinst is als de ruit vierkant is.
         
In een gebouw wil men op 100 m hoogte ruiten plaatsen waarvan de verhouding van lengte en breedte 8 : 5 is. De dikte van de ruiten moet 22 mm zijn.
         
5p. 8. Welke afmetingen kunnen de ruiten maximaal hebben? Licht je antwoord toe.
         
OPGAVE 3.  Oversteken.
         
Men heeft onderzoek gedaan naar de loopsnelheden van voetgangers. Bij dit onderzoek zijn de voetgangers in 3 leeftijdsgroepen verdeeld, nl. kinderen, volwassenen en ouderen.
Met de gegevens uit het onderzoek heeft men een boxplot gemaakt voor de loopsnelheden van de groep ouderen. Zie de volgende figuur.
         

         
De snelheden die bij de boxplot vermeld zijn, zijn in meters per seconde.
Meer gedetailleerde informatie over de groepen zie je in de volgende figuur.
         

         
Op de verticale as staat een cumulatief percentage; dit houdt in dat afgelezen kan worden hoeveel procent van de mensen van de verschillende groepen met de aangegeven snelheid of een lagere snelheid loopt.
Zo kun je bijvoorbeeld aflezen dat voor de groep ouderen bij een snelheid van 1 m/s het cumulatief percentage bijna 70 is. Dus bijna 70% van de ouderen loopt met een snelheid van 1 m/s of langzamer.

Aan de hand van onder andere deze gegevens wordt een model gemaakt voor de tijd die mensen nodig hebben om een weg over te steken.
Neem aan dat de loopsnelheden ook voor het oversteken van een weg gelden. We bekijken het oversteken van een 20 meter brede weg. Er wordt recht overgestoken, dus men loopt daarbij 20 m.
         
5p. 9. Maak met behulp van de gegevens van de boxplot hierboven een boxplot voor de oversteektijden van ouderen. Licht je werkwijze toe.
         
Tot nu toe hebben we alleen gekeken naar de tijd van het oversteken zelf. Als je bij een weg aankomt, kun je niet altijd meteen oversteken; soms moet je een aantal seconden wachten. Deze wachttijd hangt samen met de drukte op de weg en de benodigde oversteektijd. De drukte op de weg wordt aangegeven met het aantal voertuigen dat per uur passeert (voertuigintensiteit). Omdat ouderen in het algemeen minder snel lopen zal voor deze groep de benodigde oversteektijd en dus ook de verwachte wachttijd groter zal zijn dan bijvoorbeeld voor kinderen.
Er is een model gemaakt voor de samenhang tussen oversteektijd, voertuigintensiteit en verwachte wachttijd.
In de volgende figuur is dat voor zes verschillende wachttijden in beeld gebracht.
         

         
Uit deze figuur is bijvoorbeeld af te lezen dat volgens dit model bij een oversteektijd van 9 sec en een voertuigintensiteit van 700 voertuigen per uur rekening gehouden moet worden met een wachttijd van 15 sec.
         
5p. 10. Teken in onderstaande figuur de grafiek die het verband aangeeft tussen de oversteektijd en de verwachte wachttijd bij een voertuigintensiteit van 800. Teken de grafiek alleen voor wachttijden van 5 tot en met 30 sec.
         

         
We willen een beeld krijgen van de totale tijd die een rol speelt bij het oversteken van een weg van 20 m breed en een voertuigintensiteit van 800 voertuigen per uur. We spreken dan over de somtijd. Als we iemands verwachte wachttijd en zijn oversteektijd optellen krijgen we zijn somtijd.
We bekijken nu de groep van volwassenen. De hoogste snelheid die in deze groep is waargenomen is 2,6 m/s.
         
7p. 11. Wat is de langste somtijd en wat is de kortste somtijd van de 10% snelste volwassenen? Licht je antwoord toe.
         

 

OPGAVE 4.  Diversiteit.
         
In de biologie komen we het begrip 'diversiteit' tegen. De diversiteit is een getal dat iets zegt over de spreiding van soorten. Het begrip wordt niet alleen in de vrije natuur gehanteerd.

Een viskweker heeft een aantal vijvers met daarin verschillende soorten siervissen. Hoe zijn de vijvers samengesteld? De eenvoudigste manier is het tellen van het aantal verschillende soorten. In vijvers 1 en 2 zitten slechts de gewone goudvis en de sluierstaart en wel in de onderstaande verhoudingen:
         
  vijver 1 vijver 2
gewone goudvis 90% 50%
sluierstaart 10% 50%
         
Omdat vijver 1 grotendeels gevuld is met de gewone goudvis terwijl de twee vissoorten in vijver 2 gelijk verdeeld zijn, zou je vijver 2 'gemengder' kunnen noemen dan vijver 1. De vakterm voor 'gemengdheid' is  diversiteit.

Simpson gebruikte de kansrekening om diversiteit van een populatie vast te leggen met een getal. Hij stelde zich voor dat je met teruglegging willekeurig twee keer een exemplaar kiest. De diversiteit (Div) van de populatie definieerde hij als de kans dat die twee exemplaren van verschillende soorten zijn.
         
4p. 12. Laat met een berekening zien dat Div voor vijver 1 kleiner is dan voor vijver 2.
         
Hieronder is af te lezen hoe de vijvers 3 en 4 zijn samengesteld.
         
  vijver 3 vijver 4
gewone goudvis
sluierstaart
hemelkijker
leeuwekopgoudvis		 30%
30%
20%
20%		 30%
0%
50%
20%
         
Uit vijver 4 worden met teruglegging willekeurig twee vissen gehaald.
         
4p. 13. Bereken de kans dat die twee vissen van dezelfde soort zijn en bereken vervolgens de Div van vijver 4.
         
Een kweker berekent dat de Div van vijver 3 precies gelijk is aan 0,74. Bij deze vijver is de diversiteit al bijna maximaal. De maximale waarde wordt bereikt als er van elke soort evenveel exemplaren aanwezig zijn.
         
5p. 14. Controleer met een berekening dat de maximale diversiteit bij vier soorten gelijk is aan 0,75.
         
De maximale waarde van de Div hangt af van het aantal verschillende soorten.  Stel dat in een vijver n verschillende soorten zitten.
         
3p. 15. Geef een formule voor de maximale Div uitgedrukt in n.
         

 

OPGAVE 5.  Stedengroei.
         
In de figuur hier onder is de groei van de bevolking van enkele Amerikaanse en Nederlandse steden voor de periode 1890-1970 in beeld gebracht. Let speciaal op de schaalverdeling langs de verticale as. Door deze bijzondere schaalverdeling komen rechte lijnen overeen met vaste groeipercentages.
Uit de figuur rechts is het verband tussen de helling van een grafiek en het bijbehorende groeipercentage af te lezen. Dit zijn de groeipercentages per 10 jaar.
         

         
Als we de helling van de grafiek van Los Angeles in de periode 1910 - 1930 in de linkerfiguur vergelijkingen met de hellingen in de rechterfiguur, dan zien we dat de bevolking van Los Angeles in deze periode is gegroeid met ongeveer 100% per jaar.
         
5p. 16. Lees in de linkerfiguur het aantalinwoners van Los Angeles af voor de jaren 1910 en 1930 en laat met een berekening zien dat er in deze periode sprake is van een verdubbeling per 10 jaar.
         
In de periode van ongeveer 1930 tot ongeveer 1960 zijn de grafieken van Rotterdam en Amsterdam bijna evenwijdig.
         
4p. 17. Onderzoek of dit betekent dat het verschil in aantal inwoners tussen Amsterdam en Rotterdam in die periode gelijk is gebleven.
         
In 1900 was het aantal inwoners van Utrecht 107000. In 1970 waren dat er 260000. In de linkerfiguur zien we dat de grafiek van Utrecht tussen 1900 en 1970 bijna een rechte lijn is. We mogen daarom aannemen dat er sprake was van een vast groeipercentage gedurende deze periode.
         
6p. 18. Bereken het groeipercentage per jaar.
         
Voor voorspellingen op de middellange termijn heeft men behoefte aan groeipercentages per 20 jaar. De rechterfiguur geeft een aantal hellingen met daarbij de groeipercentages per 10 jaar. Bij de twee steilste staan de percentages 100 en 200.
         
6p. 19. Bereken voor deze twee de bijbehorende groeipercentages per 20 jaar.
         

 

UITWERKING
   
1.  
   
2.  
   
3.  
   
4.  
   
5.  
   
6.  
   
7.  
   
8.  
   
9.  
   
10.  
   
11.  
   
12.  
   
13.  
   
14.  
   
15.  
   
16.  
   
17.  
   
18.  
   
19.  
   
20.  
   
21.  
   
22.  
   
23.