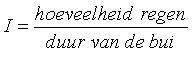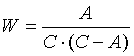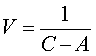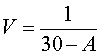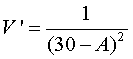HAVO WA12, 2002 - II

 

Wereldrecords nattigheid.
Wie loopt de 5000 meter in de kortste tijd? Die atleet mag zich wereldrecordhouder op de 5000 meter noemen. Op welke plaats op aarde valt in een regenbui van 7 uur het meeste water? Die plaats mag zich wereldhouder nattigheid over 7 uur noemen.

De hoeveelheid water van een regenbui wordt gemeten in inches (1 inch = 2,54 cm). Het regenwater wordt opgevangen in een regenmeter. De hoogte van het water in de regenmeter geeft aan hoeveel regen er is gevallen.
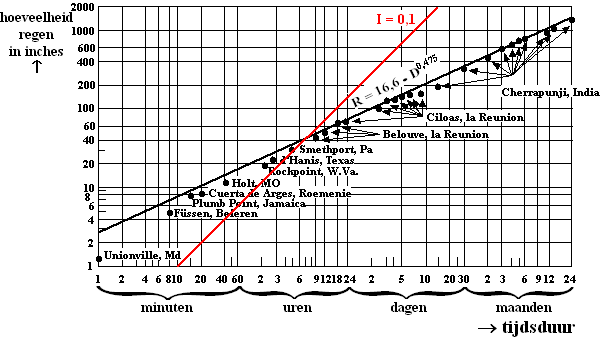
Een aantal wereldrecords nattigheid zijn met punten in onderstaande figuur weergegeven. Op de horizontale as staat hoe lang de bui geduurd heeft en op de verticale as staat de hoeveelheid regen. Men heeft langs beide assen voor een bijzondere schaalverdeling gekozen.

Plumb Point in Jamaica is één van de wereldrecordhouders.
3p

1.

 Hoe lang duurde die regenbui en hoeveel centimeter regen kwam er naar beneden?
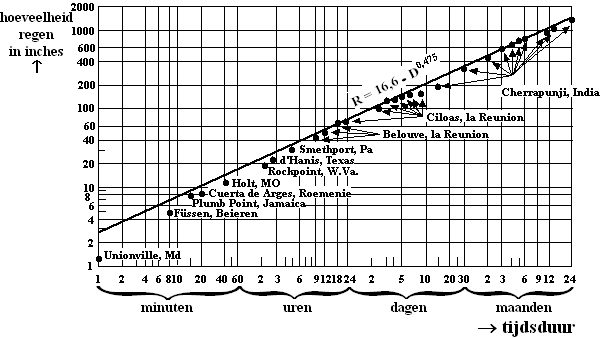
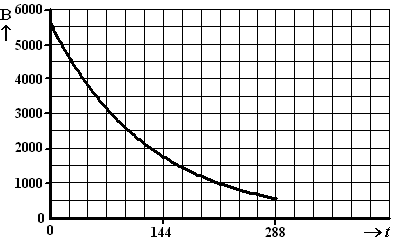
De grafiek komt uit een artikel over regenbuien. De schrijver van het artikel heeft een lijn getrokken waar geen enkele van deze wereldrecords boven ligt. Het lijkt alsof heviger regenval dan op deze lijn niet mogelijk is.

Over de punten op deze lijn beweert de schrijver:  "De hoeveelheid regen van 100-minutenbuien is ongeveer drie keer zo groot  als de hoeveelheid regen van 10-minutenbuien. De hoeveelheid regen van 1000-minutenbuien is weer ongeveer drie keer zo groot als van 100-minutenbuien".
4p

2.

 Onderzoek of deze beweringen juist zijn.
De schrijver heeft een formule voor de lijn opgesteld:
R = 16,6 • D0,475 

Hierin is R de hoeveelheid regen in inches en D de duur van de bui.
4p

3.

 Onderzoek welke eenheid D in de formule heeft:  minuten, uren, dagen of maanden.

  

In het voorgaande hebben we bij verschillende regenbuien gelet op de hoeveelheid regen en de bijbehorende tijd. In verband met overstromingsproblemen (van riolen en dergelijke) is het van belang om ook te letten op de hoeveelheid regen per minuut. Dit wordt de Intensiteit I van een bui genoemd. In formulevorm:

Hierbij is de hoeveelheid regen in inches en de duur van de bui in minuten.
2p

4.

 Bereken de intensiteit van de regenbui van Füssen uit de figuur.
Als de intensiteit I te hoog is, kunnen er problemen ontstaan met de afvoer van het water. Een intensiteit van 0,1 blijkt in de praktijk al voor grote problemen te kunnen zorgen. Punten met gelijke intensiteit liggen in bovenstaande figuur op een rechte lijn. In de figuur kan de lijn getekend worden die hoort bij I = 0,1.
5p

5.

 Onderzoek hiermee welke van de buien een intensiteit kleiner dan 0,1 hadden.

 

 

Licht in de kas.
Veel tuinbouwkassen in Nederland worden 's nachts verlicht om de groei van de planten te bevorderen. Om deze kassen te verlichten worden lampen van 600 Watt gebruikt. Per hectare (10000 m2) zijn 1000 van die lampen nodig.
Onlangs heeft een tuinder een nieuw systeem van verlichten ontwikkeld. Bij dit systeem zitten de lampen niet meer vast, maar glijden ze langs rails boven in de kas heen en weer. De planten worden verlicht zolang de lamp erboven is,  daarna staan ze weer in het donker. Met dit systeem heb je per hectare maar 60 lampen nodig, terwijl de groeibevordering nauwelijks minder is dan bij continue verlichting.

Elektriciteit betaal je per kilowattuur (kWh). 1 kWh is de hoeveelheid elektriciteit die een lamp van 1000 Watt gebruikt als hij één uur brandt. Een lamp van 600 kWh gebruikt in één uur 0,6 kWh.
Tuinders betalen 4,9 eurocent per kWh.
De lampen branden gemiddeld acht uur per etmaal (1 etmaal = 24 uur).
We houden in deze opgave geen rekening met de extra kosten voor het laten bewegen van de lampen.

4p

6.

 Bereken de jaarlijkse besparing aan elektriciteitskosten voor één hectare met dit nieuwe systeem.
Een andere tuinder is nieuwsgierig geworden en gaat het systeem in een van zijn kleinere kassen uitproberen. Hij heeft een kas met een lengte van 40 m. In de volgende figuur staat schematisch een deel van het bovenaanzicht van die kas met bewegende lampen. De lampen bewegen met een snelheid van 25 meter per uur.

In de figuur hieronder staat het zijaanzicht van één van de lampen De lamp verlicht de planten over een lengte van 5 meter.

W gaan ervan uit dat de lampen alle punten in de kas even lang beschijnen. In de maand oktober branden de lampen acht uur per nacht.
4p

7.

 Hoe lang wordt een punt in het midden van de kas verlicht tijdens een nacht in oktober? Licht je antwoord toe.

 
In een grote kas bewegen de lampen naast elkaar. Omdat alle lampen een eigen motortje hebben om zich voort te bewegen, kunnen er kleine afwijkingen zitten in de oversteektijden van de lampen. De tijd om de overkant van de kas te bereiken is normaal verdeeld met een gemiddelde van 96 minuten en een standaardafwijking van 50 seconden.

De tuinder wil het liefst dat de lampen naast elkaar heen en weer over de lengte van de kas blijven gaan. Dat is beter voor de planten. Om ervoor te zorgen dat alle lampen op het zelfde moment weer teruggaan worden ze allemaal voorzien van een klok. De klok zorgt ervoor dat de lampen precies twee minuten na de gemiddelde oversteektijd aan de terugtocht beginnen. Lampen die iets langer over de oversteek hebben gedaan staan dus iets korter stil.
Wanneer een lamp meer dan twee minuten langer voor de oversteek nodig heeft, hoeft die niet te wachten. De lamp is te laat en gaat direct terug.

Van de lampen die op tijd vertrekken komt een deel te laat aan de overkant en gaat dus direct terug.
6p

8.

 Bereken welk percentage van die lampen te laat aankomt.

 
Het komt naar de zin van de tuinder toch te vaak voor dat een lamp te laat aankomt en dus na de andere lampen weer vertrekt. Hij wil daarom de kans verkleinen dat een lamp te laat aankomt: die mag niet groter zijn dan  0,001.
Dat kan hij bereiken door de lampen meer dan twee minuten te laten wachten voor zij teruggaan. De kans op het overschrijden van die wachttijd wordt dan kleiner.
5p

9.

 Hoeveel seconden moeten de lampen dan langer wachten voor ze aan de terugtocht beginnen? Licht je antwoord toe.

 

 

Het loket.
Wij brengen heel wat tijd wachtend door: in de rij voor de kassa van de supermarkt, in de rij voor het loket in het postkantoor of  'in de wacht' aan de telefoon. Deze opgave gaat over wachttijden bij een loket.

Een postkantoor met één loket gaat op een ochtend open. Kort na elkaar komen zeven klanten binnen. We meten van deze klanten het aankomsttijdstip en de bedieningstijd in seconden. De bedieningstijd is de tijd die nodig is om de klant te helpen.
Het tijdstip van openen noemen we t = 0
De tijden van deze zeven klanten staan in de volgende tabel.
klant 1 2 3 4 5 6 7
aankomsttijdstip (seconden) 55 87 111 151 163 183 196
bedieningstijd (seconden) 43 36 34 20 6 14 26
Je ziet dat klant 1 op t = 55 seconden binnen komt. Zij wordt direct geholpen, staat 43 seconden aan het loket en is dus klaar op t = 98 seconden. Intussen is klant 2 binnengekomen. Zij moet wachten tot klant 1 klaar is. Op dat tijdstip gaat haar bedieningstijd in.
5p

10.

 Welk van de zeven klanten heeft het langst moeten wachten voor zij aan de beurt was? Licht je antwoord toe.

 
We kunnen het binnenkomen, wachten en geholpen worden van klanten in het postkantoor ook in een schema weergeven. In onderstaande figuur is de situatie weergegeven van negen klanten van het postkantoor op een andere ochtend.

Het tijdstip van aankomst en vertrek van iedere klant staat op de horizontale as. In ieder blokje staat het nummer van de klant.
Klant 1 komt op t = 38 seconden binnen en wordt direct geholpen. Klant 2 komt op t = 79 seconden binnen en moet even wachten tot klant 1 klaar is.
Als klant 4 binnenkomt op t = 134 seconden wordt klant 2 nog steeds geholpen, zodat  klant 4 achter klant 3 in de rij moet aansluiten.
Op deze manier is van alle negen klanten het verblijf in het postkantoor in beeld gebracht.
5p

11.

 Hoe lang hebben de negen klanten gemiddeld gewacht tot ze geholpen werden? Licht je antwoord toe.

 
Wiskundigen hebben een model opgesteld voor wachtrijen bij een loket. Uit dat model volgt de volgende formule voor de gemiddelde wachttijd:
• W is de gemiddelde wachttijd in uren.
• A is het aantal klanten dat gemiddeld per uur bij het loket komt.
• C is het aantal klanten dat gemiddeld per uur bediend kan worden
Bij een loket is de gemiddelde bedieningstijd één minuut. Elke tien minuten komen er gemiddeld acht mensen.
4p

12.

 Bereken de gemiddelde wachttijd in minuten.
Het model geeft ook een formule voor de tijd die men gemiddeld voor een loket verblijft, dus de wachttijd en de bedieningstijd samen.
• V is de gemiddelde verblijfstijd in uren; wachttijd plus bedieningstijd.
• A is het aantal klanten dat gemiddeld per uur bij het loket komt.
• C is het aantal klanten dat gemiddeld per uur bediend kan worden

In het vervolg van deze opgave is de gemiddelde bedieningstijd 2 minuten. Je krijgt dan voor V de formule:
3p

13.

 Bereken het aantal klanten dat gemiddeld per uur bij het loket komt als de gemiddelde verblijfstijd zes minuten is.
De afgeleide functie van V is:
3p

14.

 Bereken V'(25) en leg uit wat de betekenis van dit getal is voor de gemiddelde verblijfstijd.

 

Domino.
Een dominospel bestaat uit 28 stenen. Op de foto staan er twee afgebeeld. Op beide helften van elke steen staat met ogen een getal aangegeven van nul tot en met zes. Op de onderkanten van de stenen staat niets: als je alle stenen omkeert, zie je niet dat ze verschillend zijn. In onderstaande figuur staan alle 28 stenen afgebeeld.

Je ziet dat er maar één steen met een 5 en een 3 is. Die steen noemen we 5-3. Een steen met op beide helften het zelfde aantal ogen, zoals de 0-0, noemen we een dubbele.

Joris en Sanne gaan domino spelen. Ze leggen alle stenen omgekeerd op tafel. Ze weten niet welke steen waar ligt. Ze pakken ieder zes stenen. Degene met de hoogste dubbele begint het spel door die hoogste dubbele op tafel te leggen.

Joris pakt als eerste zes stenen. Hij vraagt zich af hoe groot de kans is dat hij geen dubbele pakt.
4p

15.

 Bereken de kans dat Joris geen dubbele pakt.

 
Als Joris en Sanne allebei geen dubbele hebben gepakt,  mag degene beginnen die de hoogste 'zes' heeft. Het eerst dus de 6-5, maar anders de 6-4, de 6-3, enzovoort. Als ze beiden zelfs geen steen met een zes hebben, mag degene met de hoogste 'vijf' beginnen, enzovoort.

Joris zegt dat hij geen dubbele heeft en dat zijn hoogste steen 6-3 is. Nu pakt Sanne haar zes stenen.
6p

16.

 Bereken de kans dat Sanne als eerste een steen  mag neerleggen.
Je kunt hierbij gebruik maken van de figuur op de bijlage.

 
Nadat ze allebei zes stenen hebben gepakt blijkt Joris met die 6-3 toch de hoogste steen te hebben. Joris legt die 6-3 op tafel. Dan is Sanne aan de beurt.
Sannen mag een steen tegen die 6-3 aanleggen,  als ze een steen heeft met een 6 of een 3 erop. Heeft ze die niet, dan moet ze net zo vaak een nieuwe steen van de stapel op tafel pakken tot ze een steen heeft waar wel een 6 of een 3 op staat. Die steen mag ze dan tegen de 6-3 op tafel aanleggen. En dan is Joris weer aan de beurt.
Een speler mag zowel aan de linkerkant als aan de rechterkant tegen de stenen op tafel een steen aanleggen, zolang hij maar een 0 tegen een 0, een 1 tegen een 1, een 2 tegen een 2,  enzovoort, legt.
Wie als eerste geen stenen meer heeft, heeft het spel gewonnen.

Na een paar beurten ligt er op tafel en rij stenen als in de volgende figuur:

Joris is begonnen met de 6-3,  de tweede steen van links. Daar zijn vijf stenen bijgekomen: aan de linkerkant de 3-2 en aan de rechterkant de 6-0, de 5-0, de 5-2 en de 4-2. Tot nu toe heeft geen van de twee spelers een steen van de stapel hoeven pakken.

Joris is nu aan de beurt. Hij heeft nog drie stenen; de 1-0, de 5-1 en de 6-1. Hij kan geen van die stenen aanleggen, want hij heeft geen 2 en geen 4. Sanne bekijkt haar drie stenen en zegt dat zij één van die drie stenen wel kan aanleggen.
Joris moet dus een steen van de stapel op tafel pakken.
4p

17.

 Bereken de kans dat hij die steen kan aanleggen.
Je kunt hierbij gebruik maken van de figuur op de  bijlage.

 
Joris vraagt zich af: als alle dominostenen omgekeerd op tafel liggen en ik pak er willekeurig twee stenen uit,  hoe groot is de kans dan dat die twee stenen op elkaar aansluiten?
Sanne legt uit dat het dan verschil maakt of de eerste steen die je pakt een dubbele is of juist niet. Immers, als je de 4-4 pakt, dan sluiten daar alleen 'vieren' op aan. Maar als je de 4-3 pakt, dan sluiten daar alle 'vieren' en alle 'drieën' op aan.
6p

18.

 Bereken hoe groot de kans is dat twee aselect gepakte stenen op elkaar aansluiten.
Je kunt hierbij gebruik maken van de figuur op de  bijlage.

 
Brandstofverbruik.
In de jaren tachtig heeft men in de Verenigde Staten een vliegtuigje gebouwd dat zonder een tussenstop om de wereld kon vliegen. Het speciaal geconstrueerde vliegtuigje vloog met een constante snelheid in 288 uur rond de aarde.
Vóór de vlucht van het vliegtuigje had men een aantal wiskundige modellen opgesteld voor de brandstofvoorraad B. Die hangt natuurlijk af van het aantal gevlogen uren t. Bij elk van die modellen ging men ervan uit dat het vliegtuigje met 5600 liter brandstof vertrekt en dat er na 288 uur vliegen nog 10% van deze totale brandstofvoorraad aanwezig is voor onvoorziene omstandigheden.

Model 1.
Bij dit model ging men ervan uit dat het brandstofverbruik (in liters per uur) constant is.
4p

19.

 Stel voor dit model een formule op voor de brandstofvoorraad B (in liters) uitgedrukt in het aantal vlieguren t.

 
Model 2.
Het gewicht van het vliegtuigje (zonder brandstof) is veel lager dan het gewicht van de 5600 liter brandstof. Tijdens de vlucht wordt het gewicht van 'vliegtuig plus brandstof ' steeds kleiner. Het vliegtuigje zal daarom tijdens  de vlucht steeds minder brandstof gaan verbruiken. Het tweede model houdt daar rekening mee.
Bij dit model hoort de formule:
B =  5600 • 0,99204t

Hierbij is B de brandstofvoorraad in liters na t uur vliegen. De grafiek die bij dit model hoort staat in de volgende figuur.

Zoals je ook in de grafiek van B kunt zien, wordt de brandstofvoorraad voortdurend kleiner.
De afgeleide dB/dt van de formule voor B geeft aan hoe de brandstofvoorraad verandert. Deze afgeleide wordt gegeven door:

Volgens model 2 is het brandstofverbruik (in liters per uur) na 24 uur vliegen ongeveer 17% lager dan aan het begin van de vlucht.
6p

20.

 Toon dit aan met behulp van de afgeleide.
Model 3.
Dit model is een aanvulling op het tweede model. Hierbij gaat men ervan uit dat na 288 uur vliegen het brandstofverbruik niet meer verandert. Zie onderstaande figuur. Het gewicht van de 560 liter brandstof is nog maar klein vergeleken met het gewicht van het vliegtuig.

3p

21.

 Bereken met behulp van de afgeleide dB/dt hoeveel uur het vliegtuigje nog door kan vliegen na 288 uur.

 
OPLOSSING
Het officiële (maar soms beknoptere) correctievoorschrift kun je HIER vinden. Vooral handig voor de onderverdeling van de punten.
1. De bui duurde ongeveer 15 minuten en er kwam ongeveer 7,9 inch = 20 cm regen naar beneden.
2. Bij 10 minuten valt ongeveer 7,8 inch
100 minuten is ongeveer 1,7 uur en daar valt iets meer dan  20 inch regen
Dat in inderdaad ongeveer drie keer zoveel.

1000 minuten is ongeveer 16,7 uur, en daar valt iets meer dan 60 inch.
Dat is inderdaad weer ongeveer drie keer zoveel.

Deze beweringen blijken aardig te kloppen.
3. D = 2 geeft R = 23 en in de grafiek zie je dat dat bij 2 uur is.  D is dus in uren.
4. Bij Füssen hoort ongeveer 8 minuten en 5 inch. I = 5/8 ≈ 0,6  inch/min
5. De lijn gaat bijv. door (10 min, 1 inch) en (18 uur, 108 inch):

De punten rechts onder de lijn hadden een kleinere intensiteit. Dat waren alle buien in Belouve, Ciloas en Cherrapunji.
6. 1 hectare kost 60 lampen die 8 uur per dag branden.
Dat is 60 • 8 • 0,6 = 288 kWh en dat kost 288 • 4,9 = 1411,20 eurocent, ofwel ongeveer 14,11 euro.

In het oude systeem is dat 1000 • 0,6 • 8 • 4,9 = 23520 eurocent ofwel 235,20 euro

De besparing per etmaal is 221,09 en per jaar is dat 365 • 221,09 = 80697,85 euro.
7. de lamp legt 5 meter af in 5/25 uur en dat is 0,2 uur. Dus per passage van de lamp wordt een plant 0,2 uur beschenen.
Over 40 meter doet een lamp 40/25 = 1,6 uur, dus in 8 uur komt een lamp 8/1,6 = 5 keer langs.
De plant wordt dus 5 • 0,2 = 1 uur beschenen tijdens een nacht.
8. normalcdf(98, 1000..., 96, 50/60) = 0,0082 dus dat is 0,82%
9. normalcdf(X, 1000..., 96, 50/60) = 0,001
Y1 = normalcdf(X, 1000..., 96, 50/60) en Y2 = 0,001
window bijv.  Xmin = 98, Xmax =110,  Ymin = 0, Ymax = 0,002
intersect levert X = 100,57 dus moeten de lampen 2,57 minuten langer wachten dan de 98 minuten van nu.
10.
klant 1 2 3 4 5 6 7
bedieningstijd 43 36 34 20 6 14 26
aankomsttijd 55 87 111 151 163 183 196
begin bediening 55 98 134 168 188 194 210
eind bediening 98 134 168 188 194 210 235

laatste rij = vierde rij + tweede rij
vierde rij overnemen uit vorige kolom (tenzij aankomsttijd later is, maar dat komt niet voor)
de wachttijden zijn het verschil tussen de derde rij en de vierde rij
Dat is respectievelijk:  0 - 11 - 23 - 17 - 15 - 11 - 14
Klant 3 moest het langst wachten
11. Alle blokjes van de tweede en derde laag samen:
(96 - 79) + (147 - 115) + (147 - 134) + (185 - 147) + (310 - 288) + (340 - 319) + (390 - 356) + (390 - 369) + (451 - 390) = 359 minuten
per klant is dat gemiddeld 359/9 = 39,89 minuten. 
12. C = 60, A = 48 geeft W = 0,0666... uur en dat is 4 minuten
13. 0,1 = 1/(30 - A)  dus  30 - A = 10  dus A = 20 klanten per uur.
14. V'(25) = 1/(30- 25)2 = 1/25 = 0,04 uur en dat is 2,4 minuten
Bij een drukte van 25 klanten per uur neemt de verblijfstijd toe met 2,4 minuten per klant extra.
15. Er zijn 7 dubbelen en 21 niet-dubbelen.
Kans op zes keer geen dubbele is  21/28 • 20/27 • 19/26 • 18/25 • 17/24 • 16/23 ≈ 0,144
16. Er liggen nog (6-4)(6-5) en 7 dubbelen waarmee Sanne eerder mag beginnen
Dat zijn 9 van de 22 stenen, dus 13 stenen waarmee Sanne NIET mag beginnen.
De kans dat Sanne NIET mag beginnen is dan 13/22 • 12/21 • 11/20 • 10/19 • 9/18 • 8/17 ≈ 0,023
De kans dat Sanne WEL mag beginnen is dan 1 - 0,023 = 0,977
17. Van de 28 stenen hebben er 13 en 4 en/of een 2.
Daarvan liggen er al 3 in de rij op tafel.
Verder heeft Sanne er nog 1.
Dus liggen er nog 9 in de stapel op tafel.
In die stapel liggen nog 28 - 12 = 16 stenen.
De kans is daarom 9/16
18. Als je een dubbele pakt (daar zijn er 7 van) sluiten daar 6 andere stenen op aan.
P(eerste dubbel én tweede sluit aan) = 7/28 • 6/27 = 42/756

Als een niet-dubbele pakt (daar zijn er 21 van) sluiten daar 12 andere stenen op aan.
P(eerste niet-dubbel én tweede sluit aan) = 21/28 • 12/27 = 252/756

samen is dat 42/756 + 252/756 = 294/756 = 7/18 ≈ 0,39
19. Een lineair verband door de punten (0, 5600) en (288, 560)
hellinggetal is  (5600 - 560)/(0 - 288) = -17,5 en beginwaarde is 5600
formule is dan  B = 5600 - 17,5t
20. t = 0 invullen in de afgeleide geeft  B'(0) = -44,75
t = 24 invullen in de afgeleide geeft  B'(24) = -36,94
Dat is  36,94/44,75 • 100% = 82,5% van het begin, dus dat is 17,5% lager
21. Bij t = 288 is het brandstofverbruik  B'(288) = -4,479 liter/uur
Er is nog 560 liter dus het vliegtuigje kan 560/4,479 = 125 uur doorvliegen.