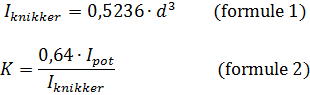Jarenlang nam in Nederland de gemiddelde lengte van volwassen mannen en vrouwen toe. Ook aan het einde van de vorige eeuw was dat nog zo: op 1 januari van het jaar 1981 waren Nederlandse mannen gemiddeld 177,3 cm lang en op 1 januari 2000 was de gemiddelde lengte toegenomen tot 180,4 cm. Dit proces verliep bij benadering lineair.
Wanneer we ervan uitgaan dat deze groei zich op dezelfde wijze voortzet, kan met behulp van lineair extrapoleren de gemiddelde lengte van de Nederlandse mannen op 1 januari 2050 berekend worden.

1.

Bereken de gemiddelde lengte van de Nederlandse mannen op 1 januari 2050.

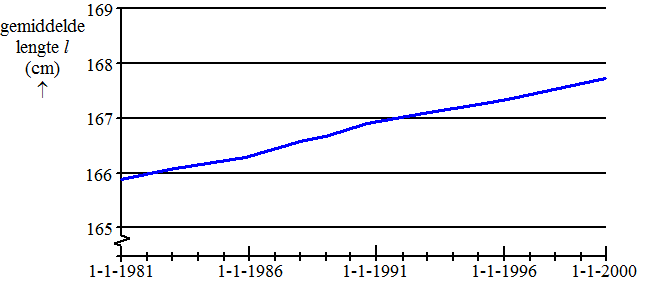
Ook de gemiddelde lengte van de Nederlandse vrouwen nam bij benadering lineair toe van 1981 tot het jaar 2000. Zie de figuur.

Hierin is l de gemiddelde lengte in cm en t de tijd in jaren waarbij geldt dat t = 0 op 1 januari 1981; a en b zijn getallen.

4p.

2.

Stel deze formule op, gebruikmakend van de gemiddelde lengte op 1 januari 1981 en de gemiddelde lengte op 1 januari 2000.

We gaan er in de volgende vraag van uit dat alle vrouwen hun lengte 0,9 cm te hoog schatten. Op basis van hun schattingen was de lengte van de Nederlandse vrouwen op 1 oktober 2000 bij benadering normaal verdeeld met gemiddelde 168,7 cm en standaardafwijking 6,0 cm. Het percentage vrouwen dat volgens hun eigen schatting langer is dan de werkelijke gemiddelde lengte van alle vrouwen, is meer dan 50%.

4p.

3.

In deze formule is G het gewicht in kg en L de lengte in meters.
Als de BMI van iemand groter is dan 25, spreekt men van overgewicht.
Uiteraard behoren mensen hun BMI te berekenen met behulp van hun werkelijke lengte en gewicht. Als mensen echter hun geschatte lengte en gewicht gebruiken, levert dat een andere BMI op.

Er is bij minder mensen sprake van overgewicht als zij hun BMI met hun eigen schattingen berekenen in plaats van met hun werkelijke lengte en gewicht.

3p.

4.

Beredeneer dit met behulp van de formule voor de BMI, zonder voor G en L getallen in te vullen.

De levensverwachting van ouderen in Nederland stijgt al jaren. Steeds meer mensen die de leeftijd van 65 jaar bereiken, worden ook 80 of 90 jaar. De kans voor een 65-jarige om de 80 of 90 te halen, wordt dus steeds groter. Voor vrouwen is deze kans nog groter dan voor mannen.
Zie de figuur.

Door gegevens uit beide grafieken te combineren, kun je berekenen hoeveel procent van de vrouwen die 65 werden in 2010, naar verwachting, wél 80 jaar maar geen 90 jaar zal worden.

4p.

5.

In het jaar 2000 is een langlopend onderzoek gestart naar de levensduur van ouderen. Er werd gestart met een onderzoeksgroep van 508 mannen en 219 vrouwen die in dat jaar 65 geworden waren. Al deze mensen waren willekeurig geselecteerd.

In de figuur is te zien dat de mannen in de onderzoeksgroep een kans van 0,52 hadden om ten minste 80 jaar te worden.

4p.

6.

Bereken de kans dat precies de helft van de mannen in de onderzoeksgroep ten minste 80 jaar wordt.

Ook kun je de kans berekenen dat meer dan 150 maar minder dan 165 vrouwen in de onderzoeksgroep de leeftijd van 80 jaar bereiken.

5p.

7.

Het langlopende onderzoek duurt voort zolang nog minimaal 50 mannen en minimaal 50 vrouwen uit de onderzoeksgroep in leven zijn. De onderzoekers vragen zich af hoe groot de kans is dat dit in het jaar 2025 het geval is.
De kans dat een willekeurige vrouw uit de onderzoeksgroep in 2025 nog in leven is, is 0,26. Dit is in de figuur af te lezen.
De kans dat er in 2025 nog minimaal 50 mannen uit de onderzoeksgroep in leven zijn, is 0,816.

5p.

8.

Bereken de kans dat het onderzoek in het jaar 2025 nog steeds voortduurt. Bereken hiervoor eerst de kans dat er in 2025 nog voldoende vrouwen uit de onderzoeksgroep in leven zijn.

Op een braderie zie je wel eens een glazen pot staan, helemaal gevuld met even grote knikkers. Tegen betaling van een bepaald bedrag mag je raden hoeveel knikkers er in de pot zitten. Degene die het aantal precies raadt of er het dichtst bij zit, wint een prijs.
Uit onderzoek blijkt dat de knikkers ongeveer 64% van de beschikbare ruimte innemen. Dit gegeven maakt het mogelijk een redelijke schatting te geven van het aantal knikkers in de pot. Hiervoor gebruiken we het volgende stappenplan:

Bepaal de diameter van een knikker en bereken daarmee de inhoud van een knikker.

Bereken 64% van de inhoud van de glazen pot en deel dit door de inhoud van één knikker. Het afgeronde antwoord is een redelijke schatting van het aantal knikkers in de pot.

Hierin is d de diameter van de knikker in cm en I_knikker de inhoud van een knikker in cm³.

Een glazen pot met een inhoud van 800 cm³ is helemaal gevuld met knikkers, die elk een diameter van 1,3 cm hebben.

3p.

9.

Geef, met behulp van het hierboven beschreven stappenplan en formule 1, een redelijke schatting van het aantal knikkers in de pot.

Het stappenplan kan worden vertaald in twee formules:

Je kunt uit de formules 1 en 2 een formule afleiden voor K, uitgedrukt in I_pot en d.
Deze formule is van de vorm:

3p.

10.

Laat zien hoe je deze formule afleidt uit de formules 1 en 2 en rond de waarde van a af op drie decimalen.

Op grond van bovenstaande gegevens kun je berekenen dat de standaardafwijking van het percentage gevulde ruimte afgerond 0,2 is.

4p.

11.

Als je precies weet welk percentage van een pot gevuld is, kun je de volgende formule gebruiken om het aantal knikkers te berekenen:

Een glazen pot met een inhoud van 1050 cm³ is helemaal gevuld met knikkers met een diameter van 0,95 cm. Het percentage gevulde ruimte p is normaal verdeeld met gemiddelde 64,0 en standaardafwijking 0,2.
Met behulp van deze gegevens kunnen we nu de kans uitrekenen dat er 1500 of meer knikkers in de pot zitten.

5p.

12.

Janneke wil op een braderie schatten hoeveel knikkers er in een glazen pot zitten. Ze herkent de glazen pot als een voorraadpot met een inhoud van 1000 cm³ en schat dat de diameter van de knikkers minimaal 1,5 cm en maximaal 1,7 cm is. Verder gaat ze ervan uit dat het percentage gevulde ruimte minimaal 63,0 en maximaal 65,0 is.

3p.

13.

Bereken het maximale aantal knikkers dat volgens de schattingen van Janneke in de glazen pot kan zitten. Licht je antwoord toe.

Met een thermosfles heb je onderweg altijd je eigen warme drank bij je.
Een consumentenblad heeft een aantal thermosflessen getest. Eén van de testonderdelen was: hoe snel neemt de temperatuur van de flesinhoud af? De flessen werden gevuld met zeer heet water en in een laboratorium in een testomgeving gezet, bij een temperatuur van 0°C. Vervolgens werd elke twee uur de temperatuur van het water gemeten.
In de volgende figuur staan de resultaten van twee thermosflessen: de thermosfles Robuust en de thermosfles Thermax.

Bij de meetresultaten van de temperatuur van het water in de Robuust is een toenamediagram getekend. Zie onderstaande figuur.

Door de gegevens uit de beide figuren  hierboven te combineren, kun je berekenen hoe hoog de begintemperatuur van het water was.

5p.

14.

De Thermax was de testwinnaar. Na 6 uur nam de temperatuur van het water in deze thermosfles af volgens een exponentieel verband. Met behulp van de gegevens in de eerste figuur kan berekend worden dat de temperatuur ieder uur met afgerond 1,8% daalde.

4p.

15.

Veel mensen vinden koffie of thee alleen lekker als de temperatuur ten minste 65°C is. Bij de Thermax bleef tijdens de test de temperatuur van het water heel lang boven die grens van 65°C.

5p.

16.

Tegenwoordig zie je vaak Quick Responsecodes, ofwel QR-codes. Door zo'n QR-code met je mobiele telefoon te 'lezen' krijg je informatie over een bepaald product of word je doorgeschakeld naar een website.
Een QR-code is een vierkante figuur die is opgebouwd uit kleine zwarte en witte hokjes, zie figuur 1. In figuur 2 zie je een uitvergroting van de linkerbenedenhoek van een QR-code. De 64 hokjes van deze hoek zijn volgens een vast patroon ingekleurd. Hetzelfde vaste patroon van 64 hokjes zie je ook in de linker- en rechterbovenhoek, maar dan gedraaid. De overgebleven hokjes van een QR-code zijn zwart of wit gekleurd afhankelijk van de informatie die de QR-code moet bevatten.

Er zijn veel meer QR-codes mogelijk waarbij de onderste regel van 21 hokjes bestaat uit 14 zwarte en 7 witte hokjes.

3p.

17.

Bereken hoeveel mogelijkheden er in totaal zijn als de eerste 8 hokjes volgens het vaste patroon zijn ingevuld.

Het verband tussen het aantal hokjes h op de onderste regel van een QR-code en het versienummer v kan worden geschreven in de vorm
h = a • v + b.

3p.

De totale ruimte die nodig is om een QR-code weer te geven, wordt niet alleen bepaald door het versienummer. Rondom elke QR-code bevindt zich een witte rand die even breed is als 4 hokjes, ongeacht het versienummer. In figuur 3 zie je hoe dat eruitziet bij een QR-code met versienummer 1. Voor de duidelijkheid zijn de hokjes getekend.

Een deel van de totale ruimte voor een QR-code wordt dus in beslag genomen door de witte rand.
Bij een QR-code met versienummer 1, zoals in figuur 3, is dat deel ongeveer gelijk aan 47,6%. Bij een QR-code met versienummer 40 is dat deel, uitgedrukt in een percentage, een stuk kleiner.

4p.

19.

Er zijn vier niveaus van foutcorrectie, zie de tabel. Van elk niveau is aangegeven hoe groot de kans is dat een licht beschadigde QR-code toch goed te lezen is.

Een postbedrijf plakt op elk postpakket een QR-code met een foutcorrigerend vermogen van niveau kwartiel. Deze pakketten komen in de meeste gevallen onbeschadigd aan bij de ontvanger. Er is echter een kans van 0,15 dat een QR-code tijdens het verzenden licht beschadigd raakt. Ga ervan uit dat uitsluitend lichte beschadigingen kunnen voorkomen.
Je kunt berekenen dat de kans dat een willekeurige QR-code na verzending nog goed te lezen is, afgerond 0,89 is.

3p.

20.

4p.

21.

Bereken de kans dat de QR-code op minimaal 90% van deze pakketten na verzending goed gelezen wordt.