1.	Ten opzichte van een rechthoekig assenstelsel XOY is gegeven de parabool met vergelijking y2 = 4x en het punt P(1, 2).
	a.	Stel de vergelijking op van de lijn die de parabool in P raakt.
	b.	Stel de vergelijking op van de cirkel waarvan het middelpunt op de Y-as ligt en die de parabool in P raakt.
2.	De rij  2,  x,  y,  x2 + 8x  bestaat uit vier verschillende termen.
	a.	Bereken x en y als de rij rekenkundig is.
	b.	Bereken x en y als de rij meetkundig is.
3.	De functies f en g zijn voor 0 ≤ x ≤ π gedefinieerd door: f(x) = 1 - sinx  en  g(x) = cos2x
	a.	Los op de vergelijking  f(x) = g(x).
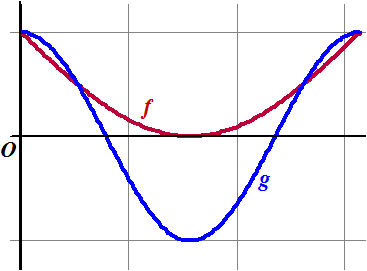
	b.	Teken in één figuur de grafieken van f en g.
	c.	De lijn x = p snijdt de grafiek van f  in A en de grafiek van g in B. De raaklijn in A aan de grafiek van f is evenwijdig aan de raaklijn in B aan de grafiek van g. Bereken sinp.
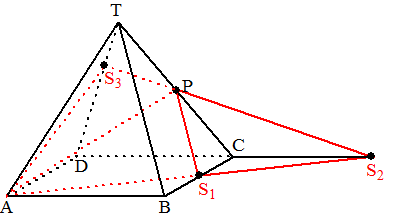
4.	In een regelmatige vierzijdige piramide T.ABCD zijn alle ribben even lang. Het midden van de ribbe CT is het punt P. Neem AB = 8 cm.
	a.	Construeer in een stereometrische figuur van de piramide de doorsnede van de piramide met het vlak dat door A en P gaat en dat evenwijdig aan BT is.
	b.	Bereken  ∠BPD.
5.	De functie f  is voor -3 < x < 5 gedefinieerd door:
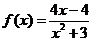	a.	Bereken de hoek waaronder de grafiek van f de x-as snijdt.
	b.	Bereken de uiterste waarden van deze functie en onderzoek van welke aard deze uiterste waarden zijn.
6.	Beschouw ten opzichte van een rechthoekig assenstelsel XOY de verzameling V van de punten (x, y) waarvoor geldt: x  ≥ 0  en  1 ≤ y ≤ 5  en   x + y ≤ 6
	a.	Teken en arceer de verzameling V.
	b.	Teken de deelverzameling van V waarvoor geldt:  x + 2y = 6. Teken de deelverzameling van V waarvoor geldt:  x + 2y = 8.
	c.	Wat is de maximale waarde die x + 2y kan aannemen?

UITWERKING
1a.	2ydy = 4dx  dus   dy/dx = 4/2y = 2/y yP = 2  dus de helling van de raaklijn is  2/2 = 1 De raaklijn is de lijn  y = x + b  en moet door (1, 2) gaan 2 = 1 • 1 + b  geeft  b = 1 De raaklijn is de lijn  y = x + 1
1b.	De parabool heeft in P helling 1  (vraag 1a) Als de cirkel de parabool raakt, dan heeft de raaklijn aan de cirkel dus ook helling 1 Dan heeft de lijn MP helling -1 want die staat daar loodrecht op MP is dus de lijn  y = -x + b en moet door (1, 2) gaan 2 = -1 + b geeft  b = 3  dus MOP is de lijn y = -x + 3 Snijden met de y-as:    M = (0, 3) MP = √(12 + 12) = √2  en dat is de straal van de cirkel. De vergelijking is dan   x2 + (y - 3)2 = 2
2a.	Als de rij rekenkundig is zijn de verschillen constant. x - 2 =  y - x  =  x2 + 8x - y Het eerste gelijkteken geeft   y = 2x - 2 Dan geeft de eerste gelijkstellen aan de laatste:   x - 2 = x2 + 8x - 2x + 2 x2 + 5x + 4 = 0 (x + 4)(x + 1) = 0 x = -4  Ú  x = -1 x = -1  geeft de rij  2,  -1,  -4,  -7 x = -4  geeft de rij  2, -4, -10, -16 Dat klopt dus  de mogelijkheden zijn  (x = -1  en y = -4)  of  (x = -4  en  y = -10)
2b.	Als de rij meetkundig is zijn de factoren constant. x/2 =  y/x  =  (x² + 8x)/y Het eerste gelijkteken geeft  x2 = 2y  dus  y = 1/2x2 Het tweede gelijkteken geeft  y2 = x(x2 + 8x) eerste invullen in de tweede:  1/4x4  = x3 + 8x2 x4 - 4x3 - 32x2  = 0 x2 (x2 - 4x - 32) = 0 x2 (x - 8)(x + 4) = 0 x = 0  Ú  x = 8  Ú  x = -4 De eerste vervalt. x = 8  geeft  y = 32 en de rij   2, 8, 32, 128 x = -4 geeft  y = 8  en de rij   2, -4, 8, -16   Dat klopt dus  de mogelijkheden zijn  (x = -8  en y = -32)  of  (x = -4  en  y = 8)
3a.	1 - sinx  = cos2x 1 - sinx = 1 - 2sin2x 2sin2x  - sinx = 0 sinx(2sinx - 1) = 0 sinx = 0  sinx = 1/2 x = 0  Ú x = p  Ú  x = 1/6p  Ú  x = 5/6p
3b.
3c.	Als de raaklijnen evenwijdig zijn hebben de functies dezelfde afgeleide bij x = p f ' (p) =  -cosp g '(p) = -2sin2p -cosp = -2sin2p cosp - 2sin2p = 0 cosp - 4sinpcosp = 0 cosp • (1 - 4sinp) = 0 cosp = 0  Ú   sinp = 1/4 dan is  sinp = 1  Ú  sinp = -1  Ú  sinp = 1/4 Maar met p tussen  0 en p geeft dat  sinp = 1  Ú  sinp = 1/4
4a.	PS1 evenwijdig aan BT  (in vlak TBC) Het gaat om de doorsnede van vlak AS1P met de piramide. Grondlijn AS1 snijden met DC geeft S2 S2P snijden met TD geeft S3 De doorsnede is AS1PS3
4b.	Neem alle zijden bijvoorbeeld  2. BP = Ö(22 - 12 ) = Ö3 BD = Ö(22 + 22) = Ö8 = 2Ö2 S is het midden van BD BS = Ö2 In PSB:   sin(0,5BPD) = Ö2/Ö3 Dat geeft  0,5BPD = 54,73º BPD = 109º
5a.	y = 0  geeft  4x - 4 = 0  dus  x = 1 f '(x) = (4(x² + 3) - (4x - 4) • 2x)/(x² + 3)² f '(1) = 16/16 = 1 tana = 1  dus de hoek is 45°
5b.	f '(x) = (4(x² + 3) - (4x - 4) • 2x)/(x² + 3)²  f '(x) = 0  geeft  4(x2 + 3) - 2x(4x - 4) = 0 4x2 + 12 - 8x2 + 8x = 0 x2 - 2x - 3 = 0 (x - 3)(x + 1) = 0 x = 3  ∨  x = -1 tekenbeeld van f':     -----(-1)+++++++(3)------- f  bereikt voor x = -1  een  minimum van  y = -2  f  bereikt voor x = 3 een maximum van y = 2/3
6a.