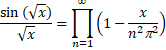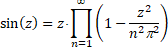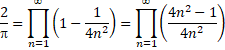© h.hofstede (h.hofstede@hogeland.nl)

De formule van Wallis
       
Daarvoor moeten we eerst even de productformule voor sinz  van Euler afleiden.

Euler begon met de reeksontwikkeling voor sinx:
En toen had hij een geniale ingeving:  hij dacht "Als ik nou x vervang door √x dan worden die machten van x groter met in plaats van 2 machten per stapje nog maar met 1 macht per stapje". Om de machten mooi geheel te maken, bekeek Euler de reeksontwikkeling voor  sin√x/√x :

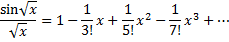Oké;  mooi oplopende machten, maar wat heb je eraan?

Het mooie komt als je de nulpunten van sin√x/√x gaat opsporen.
Dat is nul als  √x = π, 2π, 3π, 4π, .....  dus dan is x = π2 , 4π2, 9π2, 16π2, .....  (niet bij x = 0  want  sinx/x gaat naar 1 voor x naar 0)
Dus moet dat polynoom daar ook de nulpunten hebben.
Dan kun je dat polynoom schrijven als   (1 - x/π˛) • (1 - x/4π˛) • (1 - x/9π˛) • (1 - x/16π˛)    ....    (dat zegt de factorstelling, want de eerste term van de reeks is 1)

Noem nu √x = z, dat geeft Euler's sinusformule:
 

 
Vul nu voor x de waarde 1/2π in.

Zet de boel op zijn kop:
 
       
       

© h.hofstede (h.hofstede@hogeland.nl)