© h.hofstede (h.hofstede@hogeland.nl)

       
1. a.
t 0 5 10 15 20
A(t) 50 570 3116 4775 4982
5000 - A 4950 4430 1884 225 18
(5000 - A)/A 99 7,77 0,60 0,047 0,0036
 
       
    De groeifactoren van de laatste rij zijn  7,77/99 = 0,078  en   0,60/7,77 = 0,078  en  0,047/0,60 = 0,078  en  0,0036/0,047 = 0,077
Dat is allemaal ongeveer gelijk aan g = 0,078  dus is de groei logistisch
       
  b. (5000 - A)/A = 99 • 0,078t    (exponentieel met g = 0,078 en B = 99)
5000 - A = 99A • 0,078t 
A(1 + 99 • 0,078t) = 5000
A = 5000/(1 + 99 • 0,078t)
       
2. a.
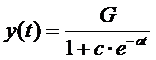    als t groter wordt, dan wordt  e-at  kleiner als a (positief is)
dus wordt 1 + c • e-at  ook kleiner  (c is ook positief)
dan wordt  G/noemer dus juist weer groter (delen door een kleiner getal)

Dus als t groter wordt, wordt y ook groter, dus de grafiek van y(t) stijgt.
       
  b. Hij beweert dus:  y0 + c • y0 =  G

maar  y0 =  y(0) =  G/(1 + c • e0)  = G/(1 + c)
dus  y0 + c • y0 =  G/(1 + c) + c • G/(1 + c) = G • (1/(1 + c) + c/(1 + c)) = G • (1 + c)/(1 + c) = G
Het blijkt te kloppen. 
       
  c. 0,5G = G/(1 + ce-at)   geeft  1 + ce-at = 2
ce-at = 1
e-at = 1/c
-at = ln(1/c) = -lnc
at = lnc
t = lnc/a
       
3.
jaar 1927 1960 1974 1987 1999 2011 2025 2041 2063
t 27 60 74 87 99 111 125 141 163
wereldbevolking (in miljarden) 2 3 4 5 6 7 8 9 10
(11,5 - y)/y 4,750 2,833 1,875 1,300 0,917 0,643 0,438 0,278 0,150
       
 

Dat geeft achtereenvolgens:
1927 - 1960:  g33 = 2,833/4,750  dus  g = 0,984
1960 - 1974:  g14 = 1,875/2,833 dus  g = 0,971
1974 - 1987:  g13 = 1,300/1,875  dus  g = 0,972
1987 - 1999:  g12 = 0,917/1,300 dus  g = 0,971
1999 - 2011:  g12 = 0,643/0,917  dus g = 0,971
2011 - 2025:  g14 = 0,438/0,643  dus  g = 0,973
2025 - 2041:  g16 = 0,278/0,438  dus  g = 0,972
2041 - 2072:  g22 = 0,150/0,278  dus  g = 0,972
g is steeds ongeveer gelijk aan 0,97  (de eerste waarde is mogelijk gevolg van een afronding)

Om B te berekenen kun je een punt uit de tabel invullen in  y = B • 0,97t   Dus  B = y/0,97t
Dat geeft:
       
 
t 27 60 74 87 99 111 125 141 163
(11,5 - y)/y 4,750 2,833 1,875 1,300 0,917 0,643 0,438 0,278 0,150
B 10,8 17,6 17,9 18,4 18,7 18,9 19,7 20,4 21,5

Door afwijkingen in g scheelt dat nogal. Neem ongeveer B = 18
Dat geeft  y =  11,5/(1 + 18 • 0,97t)
       
4. a. maak een tabel met de groeifactoren:  
       
   
t 0 5 10 15 20 25 30 35 40 45 50
N 110 141 181 232 296 377 477 602 754 938 1155
N(t + 1)/N(t)   1,3 1,3 1,3 1,3 1,3 1,3 1,3 1,3 1,2 1,2
       
    Voor  0 < t < 40  blijft g (in ιιn decimaal) ongeveer gelijk dus is er sprake van exponentiλle groei.
       
  b. Plot  Y1 = 5600/(1 + 50 • 0,95^X)
Y2 = Y1(X) - Y1(X - 1)  dat geeft de toename van Y1
Y3 = Y2(X) - Y2(X - 1)  dat geeft de toename van Y2
Kijk bij TABLE wanneer Y3 positief is (dat is als Y2 toeneemt; daar kun je ook naar kijken)
Dat is zo voor  t < 78
       
5. G = 140, dus  y  = 140/(1 + B • gt)
t = 0  geeft  50 cm,  dus  50 = 140/(1 + B • g0) = 140/(1 + B)  dus  1 + B = 2,8  dus B = 1,8
t = 15 geeft  0,95 • 140 = 133
Dus  133 = 140/(1 + 1,8 • g15)
1 + 1,8 • g15  = 1,0526
1,8 • g15 = 0,0526
g15 = 0,0292
g = 0,79
y = 140/(1 + 1,8 • 0,79t)

Zij groeit het snelst op het buigpunt, en dat is bij y = 0,5G = 70
70 =  140/(1 + 1,8 • 0,79t)
1 + 1,8 • 0,79t = 2
1,8 • 0,79t = 1
0,79t = 0,5555
t = log(0,5555)/log(0,79) = 2,5 jaar
       
6. a. Invoeren in de GR (MODE SEQ)
nmin = 0
u(n) = u(n-1) + 0,3•u(n - 1)•(1 - u(n-1)/10,9)
u(nmin) = 6,1
Dan in de tabel kijken levert als grenswaarde 10,9 miljard (vanaf ongeveer n= 28)
In 2050 (n= 5) zijn er 9,42 miljard
Dat scheelt 1,48 miljard en dat is  1,48/10,9 • 100% = 13,6%
In 2050 is de bevolking dus meer dan 10% van de grenswaarde verwijderd.
       
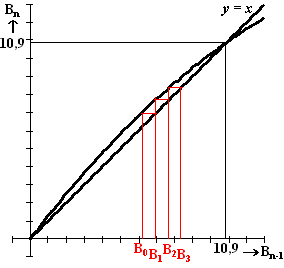
  b.  
    Begin bij B0 = 6,1 op de x-as. Ga omhoog tot de gekromde grafiek, daarna opzij naar de lijn y = x
Bij dit punt hoort B1 op de x-as.
Ga weer omhoog naar de gekromde grafiek, en weer opzij naar y = x, enz.
       
  c. Stel de bevolking in 1990 gelijk aan x, dan geldt:
6,1 = x + 0,3x • (1 - x/10,9)
6,1 = x + 0,3x - 0,3x • x/10,9  ⇒  6,1 = 1,3x - 0,0275x2  ⇒  0,0275x2 - 1,3x + 6,1 = 0
ABC-formule levert nu  x = 41,99 V x = 5,28 en dat laatste is het juiste antwoord.
(met de GR Y1 = 6,1 en Y2 = x + 0,3x • (1 - x/10,9) en dan intersect kan ook natuurlijk)
In 1990 was de wereldbevolking 5,28 miljard.
       
7. a. c = 165/500 = 0,33
Het is een meetkundige rij
Daarvan is de directe formule  P(n) = 0,33 · 1,26n 
 0,33 · 1,26n  = 1
1,26n = 3,0303...
n = log(3,0203...)/log(1,28) = 4,49
Dus na 5 jaar is het maximale aantal bereikt.
       
  b. P0 = 0,25
P1 = 1,58 · 0,25 · (1 - 0,25 = 0,29625
P2 = 1,58 · 0,29625 · (1 - 0,29625) = 0,3294
Het maximum is 2000 dus dit zijn 658 α 659 edelherten
Vanaf de 500 zijn er dus  158 α 159 bijgekomen.
       
  c. r en Pn en  1 - Pn liggen alle drie tussen 0 en 1  (en zijn alle drie positief)
Als je ze met elkaar vermenigvuldigt wordt dat dus steeds kleiner.
Het blijft wel positief, dus gaat dat naar nul.
       
  d. Voer de recursieformule in in de GR:
MODE - SEQ
Y=
nMin = 0
u(n) = 3,15· u(n - 1) · (1 - u(n - 1))
u(0) = 0,25
Kijk dan in de tabel bij grote waarden van n
Dan zie je dat Pn heen en weer gaat tussen 0,78 en 0,53
       

© h.hofstede (h.hofstede@hogeland.nl)