© h.hofstede (h.hofstede@hogeland.nl)

       
1. a.

       
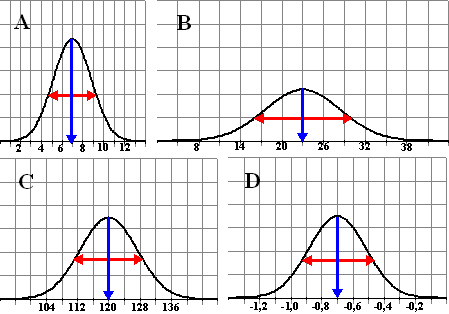
    μ bij de blauwe pijl.
De lengte van de rode pijl (zo goed mogelijk bij het buigpunt getekend) is 2σ.

A:  μ = 7,   σ = 2,5
B:  μ = 23,  σ = 7,5
C:  μ = 120,  σ = 9
D:  μ = -0,7,  σ = 0,25
       
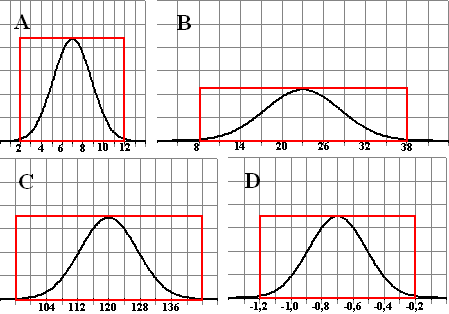
  b. De totale oppervlakte moet steeds 1 zijn.
Teken er een rechthoek omheen:
       
   

       
    A:  de breedte is 10, en de klokvorm is ruwweg de helft van de oppervlakte.
Dus moet de oppervlakte 2 zijn, dus de hoogte ongeveer  0,2
De schaalverdeling is waarschijnlijk 0,05 per hokje

B:  de breedte is 30, en de klokvorm is ruwweg de helft van de oppervlakte.
Dus moet de oppervlakte 2 zijn, dus de hoogte ongeveer  0,07
De schaalverdeling is waarschijnlijk 0,03 per hokje

C:  de breedte is 48, en de klokvorm is ruwweg de helft van de oppervlakte.
Dus moet de oppervlakte 2 zijn, dus de hoogte ongeveer  0,04
De schaalverdeling is waarschijnlijk 0,01 per hokje

D:  de breedte is 1, en de klokvorm is ruwweg de helft van de oppervlakte.
Dus moet de oppervlakte 2 zijn, dus de hoogte ongeveer 2
De schaalverdeling is waarschijnlijk 0,5 per hokje
       
2. De totale oppervlakte moet 1 zijn, dus als de klokvorm hoger is moet hij wel smaller zijn anders zou die oppervlakte te groot worden.
       
3.

       
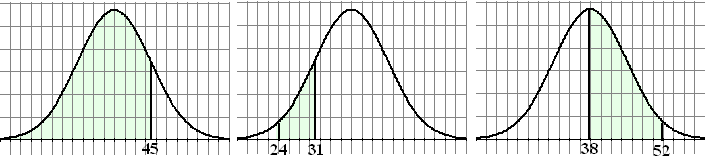
  a. alles onder  μ + σ  en dat is 68% + 16% = 84%
       
  b. alles tussen  μ - 2σ en μ - σ  en dat is  16% (links van 31) - 2,5% (links van 24) = 13,5%
       
  c. alles tussen m en  μ + 2σ  en dat is  97,5% (links van 52) - 50% (links van 38) = 37,5%
       
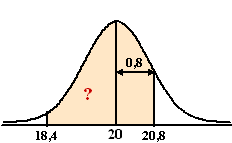
4. a. Zie de oppervlakte hiernaast.
Het is het gebied tussen  μ - 2σ  en  μ + σ
Dat is  84% (links van 20,8) - 2,5% (links van 18,4) = 81,5%
       
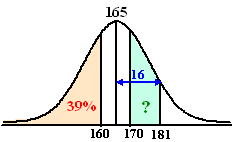
  b. Als het gebied links van 160 gelijk is aan 39%, dan is vanwege de symmetrie van de klokvorm het gebied rechts van 170 ook 39%
Tussen 165 en 181 zit 34%, dus rechts van 181 zit 16%

Dan zit tussen 170 en 180 dus  39% - 16% = 23%
       
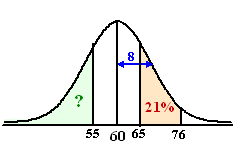
  c. 76 is gelijk aan m + 2σ, dus rechts ervan zit 2,5%
Dan zit rechts van 65 dus  21 + 2,5 = 23,5%

Dat zit ook links van 55 (symmetrie van de klokvorm)
Dus links van 55 zit 23,5%
       
5. a. NEE.  er zijn niet evenveel mensen met een hoog inkomen als met een laag inkomen. De inkomensverdeling is niet symmetrisch!
       
  b. JA  
       
  c. JA  
       
  d. JA  
       
  e. NEE. De afstand kan niet onder nul, en er wonen wel redelijk wat kinderen dicht bij school, dus de staart van de verdeling naar links stopt bij nul.
       
  f. JA  
       
  g. NEE. De meeste mensen betalen vrij snel hun rekening, dus bij kleine tijden zal de verdeling hoog zijn, en naar rechts toe steeds lager worden. Bovendien kan ook nu onder nul dagen niet voorkomen.
       
6. Als iedereen in Nederland samen zo'n klokvorm vormt, dan zijn de VWO leerlingen daar het rechterdeel van (dat zijn voornamelijk de leerlingen met een hoger IQ)
Het rechterdeel van een klokvorm kan zelf niet weer een klokvorm zijn!
       
7. Het gemiddelde is bij vrouwen hoger, dus het midden van de klokvorm bij vrouwen moet meer naar rechts liggen dan bij mannen. 
De standaardafwijking bij mannen is kleiner dan bij vrouwen, dus de klokvorm van de mannen is smaller (en daardoor ook hoger, want de totale oppervlakte blijft natuurlijk 100%)
Figuur 1 is de enige waarbij de klokvorm die het meest links ligt ook het smalst is. Dat is 'm dus.
       
       

© h.hofstede (h.hofstede@hogeland.nl)