© h.hofstede (h.hofstede@hogeland.nl)

       
       
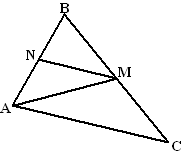
1. AN + NM ≥ AM  (driehoeksongelijkheid)
NM = 1/2AC,  en AN = 1/2AB
Dus 1/2AB + 1/2AC ≥ AM
1/2(AB + AC) ≥ AM
       
2. AB + BC ≥ AC  (driehoeksongelijkheid)
AC + CD ≥ AD  (driehoeksongelijkheid)
Dus AB + BC + CD ³ AD
of:  "de kortste route van A naar D is een rechte lijn"
       
3. AP + PB ≥ AB   (driehoeksongelijkheid)
BP + PC ≥ BC   (driehoeksongelijkheid)
CP + PA ≥ CA   (driehoeksongelijkheid)
optellen:  2AP + 2BP + 2CP ≥ AB + BC + CA  en dat laatste is de omtrek van de driehoek.
dus 2(AP + BP + CP) ≥ omtrek
       
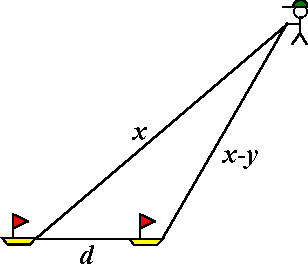
4. Stel dat het touw lengte x heeft, en dat kleine Karel het touw y meter inneemt.
Dan geldt de situatie hiernaast.

De driehoeksongelijkheid levert  d + x - y  > x
En daaruit volgt:

d > y

ofwel in woorden: de afstand tot de oever (d) is groter dan de hoeveelheid ingenomen touw (y)

       
5. noem de zijden a, b en c. En kies als willekeurige zijde a.
driehoeksongelijkheid:  b + c  ≥  a
tel bij beide kanten a op:
a + b + c ≥ 2a
a ≤ 1/2(a + b + c) = 1/2 • omtrek.
       
6. Noem de drie zijden x, 3x en 15.
Dan zijn er drie driehoeksongelijkheden waaraan voldaan moet worden:

x + 3x > 15  geeft  x > 3,75
x + 15 > 3x  geeft  15 > 2x dus  x < 7,5
3x + 15 > x geeft  2x > -15 en x > -7,5

De maximaal mogelijke x volgt uit de tweede voorwaarde en dat is x = 7
Dat geeft zijden 7 - 15 - 21
De omtrek is dan 43
       
7. a. a + d + z = 4,7   (1)
a + b + z = 5,7   (2)
b + c + z = 4,3   (3)

(1) geeft a = 4,7 - d - z
(3) geeft  b = 4,3 - c - z
en dat kun je invullen in (2):

4,7 - d - z  + 4,3 - c - z  + z = 5,7
d + c + z = 4,7 + 4,3 - 5,7 = 3,3 en dat is de omtrek van PCD
       
  b. b + c + z = 3,3
Maar z < b + c dus z is minder dan de helft van 3,3
Dus z < 1,65

a + b + z  is de omtrek van  PAB en die is 5,7
Als z < 1,65 dan moet wel gelden dat a + b > 5,7 - 1,65 = 4,05
       
  c. Stel dat a de langste zijde is van a en b
Dan is  a > 4,05/2 = 2,33
Punt P bevindt zich dan in de onderste helft van vierkant ABCD.
De langste lijn die daarin te tekenen is, is als z = 1,65 en is gelijk aan √(1,652 +  (0,5 •1,65)2) = 2,02
Dat kan dus nooit 2,33  worden....
(als b de langste zijde is, geldt uiteraard precies zo'n verhaal)
       
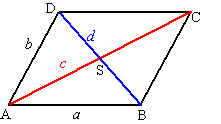
8. Noem de zijden a en b en de diagonalen c en d

AD ≤  AS + SD  dus  b ≤ 1/2c + 1/2d
AB ≤ AS + SB  dus  a ≤ 1/2c + 1/2d

Tel die twee op:   a + b  ≤ c + d

       
9. Vermenigvuldig van de linkerkant teller en noemer steeds met 2, dan krijg je:
 
       
  Omdat a < b + c  en  b < a + c  en  c < a + b  worden de noemers kleiner als je één van beide termen vervangt door de derde zijde (dus vervang a + b door c   enz.)
Als de noemers kleiner worden, dan worden de drie breuken groter.
       
 
       
  en dat moesten we bewijzen!
       

© h.hofstede (h.hofstede@hogeland.nl)