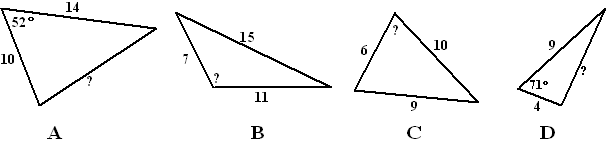|
|||||
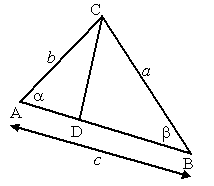
| 1. | cosα
= AD/b ⇒ AD
= bcosα AD2 + CD2 = b2 ⇒ b2cos2α + CD2 = b2 ⇒ CD2 = b2 - b2cos2α DB = AB - AD = c - bcosα DB2 + CD2 = CB2 |
 |
|||
| 2. |
|
||||
| A. | x2 = 102 + 142 - 2 10 14 cos52º = 123,61 ⇒ x = √123,61 = 11,1 | ||||
| B. | 152 = 72
+ 112 - 2 7 11 cosα 225 = 170 - 154cosα 55 = -154cosα cosα = -0,357 α = 110,9º |
||||
| C. | 92 = 102 +
62 - 2 10 6 cosα 81 = 136 - 120cosα -55 = -120cosα cosα = 0,458 α = 62,7º |
||||
| D. | x2 = 42 + 92 - 2 4 9 cos71 = 73,56 ⇒ x = √73,56 = 8,6 | ||||
| 3. |
|
||||
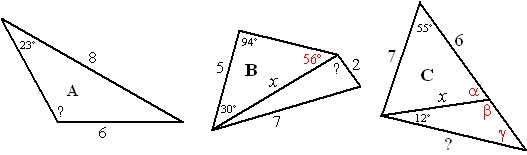
| A. | 6/sin23
= 8/sinα sinα = 8 sin23/6 = 0,521 α = 31,4º maar je moet de hoek 180 - 31,4 = 148,6º hebben |
||||
| B. | 5/sin56
= x/sin94 x = sin94 5/sin56 = 6,016 72 = 22 + 6,0162 - 2 2 6,016 cosα 49 = 40,197 - 24,066 cosα 8,803 = - 24,066 cosα cosα = -0,366 α = 111,5º |
||||
| C. | x2
= 62 + 72 - 2 6 7 cos55 = 36,82
Þ x =
√36,82 = 6,07 7/sinα = x/sin55 sinα = 7 sin55/6,07 = 0,945 α = 70,90º dan is β = 109,09º en γ = 58,91º 7/sinγ = ?/sin55 ? = sin55 7/sin58,91 = 6,7 |
||||
| 4. | voor de hoek bij A
geldt: 72 = 92 + 32 - 2 9 3
cosα 49 = 90 - 54cosα -41 = -54cosα cosα = 0,759 α = 40,6º sin(40,6) = CD/3 CD = 3 sin40,6 = 1,95 |
||||
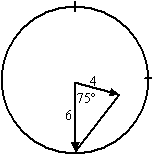
| 5. | De hoek is dan 75º. x2 = 42 + 62 - 2 4 6 cos75 = 39,58 x = √39,58 = 6,29 cm |
|
|||
| 6. | a. | D heeft maximale hoogte als B
recht onder C staat. ABC en AED zijn gelijkvormig BC/CA = DE/DA 60/100 = DE/130 DE = 130 60/100 = 78 cm hoog |
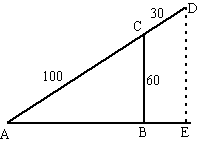 |
||
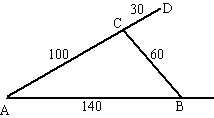
| b. | De situatie is dan als hiernaast. Helemaal ingeklapt was AB = 160, dus nu is AB = 140 602 = 1002 + 1402 - 2 100 140 cosα 3600 = 29600 - 28000 cosα -26000 = -28000cosα cosα = 0,928 α = 21,79º en dat is hoek BAC. sin(21,79) = hoogteD/130 hoogte D = 130 sin(21,79) = 48,2 cm gaat D omhoog |
 |
|||
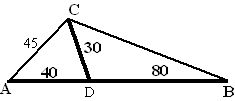
| 7. | in driehoek ACD: 302 = 402 + 452 - 2 40 45 cosα 900 = 3625 - 3600 cosα -2725 = -3600cosα cosα = 0,757 α = 40,80º in driehoek ACB: BC2 = 452 + 1202 - 2 45 120 cosα BC2 = 8250 BC = 90,8 meter |
 |
|||
| 8. |
|
||||
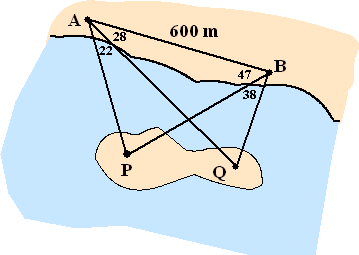
| ∠BQA
= 180 - 28 - 47 - 38 = 67º driehoek BQA: 600/sin67 = AQ/sin85 ⇒ AQ = sin85 600/sin67 = 649,34 ∠APB = 180 - 22 - 28 - 47 = 83º driehoek APB: 600/sin83 = AP/sin47 ⇒ AP = sin47 600/sin83 = 442,11 driehoek PQA: PQ2 = 442,112 + 649,342 - 2 442,11 649,34 cos22 = 84751,13 Dan is PQ = √84751,13 = 291 meter |
|||||
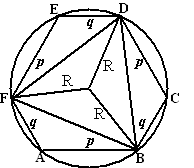
| 9. | De hoeken van de
zeshoek zijn allemaal 120º, want alle hoeken zijn gelijk (steeds de hoek
tussen een zijde p en een zijde q) Binnen de cirkel is nu een gelijkzijdige driehoek met zijden z te zien. Cosinusregel: z2 = p2 + q2 - 2pqcos 120º en ook z2 = R2 + R2 - 2RRcos120º samennemen, en invullen cos 120º = -0,5 geeft: p2 + q2 + pq = 3R2 ofwel R = √(1/3(p2 + pq + q2)) |
 |
|||
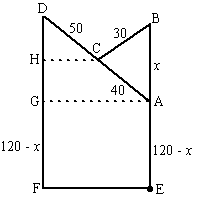
| 10a. | Als AB = x dan
is AE = 120 - x driehoek ABC: 302 = 402 + x2 - 2 40 x cos∠CAB 80x cos∠(CAB) = 700 + x2 cos∠CAB = (700 + x²)/80x maar dat is ook cos∠ADG want die hoeken zijn gelijk (Z-hoeken) in driehoek AGD: cos∠ADG = DG/90 ⇒ DG = 90 cos∠ADG dat geeft DG = 90 (700 + x²)/80x = 787,5/x + 9/8x |
 |
|||
| DF = h = DG + GF = 787,5/x + 9/8x + 120 - x = 787,5/x + 1/8x + 120 | |||||
| 10b. | De stijg/daalsnelheid
is h ' h ' = (-787,5 x-2 + 1/8) x' Als x afneemt, dan is x' negatief -787,5 x-2 + 1/8 = 0 x-2 = 0,000159 x = 79,4 Als x < 79,4 (en dat is altijd zo, want x < 70), dan is -787,5 x-2 + 1/8 negatief, dus als x' negatief is, dan is h' positief is h' positief, dus stijgt D |
||||
|
© h.hofstede (h.hofstede@hogeland.nl) |
|||||