|
|||||
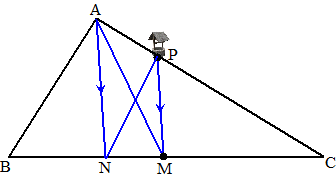
| 1. | a. | De basis van beiden is gelijk,
want AM = AC De hoogte van beiden is gelijk, namelijk de hoogtelijn van A op BC Dus zijn de oppervlakten gelijk. |
 |
||
| b. | Kies als basis PM Dan is de hoogte van beiden de afstand tussen de evenwijdige lijnen PM en AN. Die is vanaf A natuurlijk gelijk aan vanaf N |
||||
| c. | PNC = PNM + PMC AMC = AMP + PMC Omdat PNM = AMP (vraag b)) is dus ook PNC = AMC en dat is volgens a) de helft van de driehoek ABC. |
||||
| 2. |
|
||||
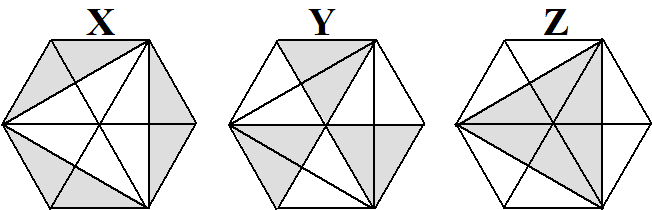
| Alle grijze
driehoekjes zijn nu even groot en elke figuur heeft er zes. Dus X = Y = Z |
|||||
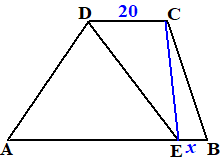
| 3. | Stel dat de hoogte van het
trapezium h is, dan is de oppervlakte ervan 35h,
dus elk deel heeft oppervlakte 17,5h driehoek DCE heeft oppervlakte 10h driehoek EBC moet dus oppervlakte 7,5h hebben Dus EB = 15 dus AE = 35 |
|
|||
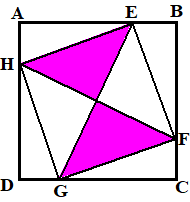
| 4. | Haal eerst bij ieder hoekpunt een
rechthoekige driehoek van het vierkant af. De zijde van het vierkant is √80 De oppervlakte van zo'n driehoek is 0,5 (1/4√80) (3/4√80) = 7,5 Dan blijft er een nieuw vierkant met oppervlakte 80 - 4 7,5 = 50 over. Het paarse gebied is daar de helft van, dus heeft oppervlakte 25. |
|
|||
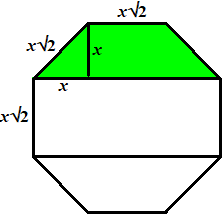
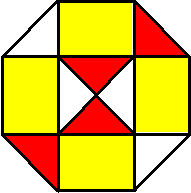
| 5. | Als de aangegeven lijnstukken
hiernaast gelijk zijn aan x, dan zijn de zijden van de achthoek
gelijk aan x√2 Het groene deel heeft oppervlakte 3 = x2 + x2√2 3 = x2(1 + √2) De middelste strook heeft oppervlakte (2x + x√2) x√2 Dat is 2x2√2+ 2x2 = 2 x2(1 + √2) en dat is precies tweemaal de groene oppervlakte. De hele achthoek heeft dan oppervlakte 3 + 6 + 3 = 12 |
|
|||
| Overigens: in het plaatje hiernaast kun je in één keer zien dat de groene oppervlakte een kwart van de hele achthoek is. |
|
||||
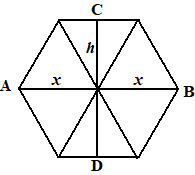
| 6. | zes driehoeken zijn samen 60 6 0,5xh = 60 xh = 20 AB CD = 2x 2h = 4xh = 80 |
|
|||
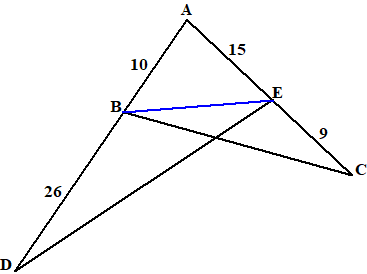
| 7. | ABE en ADE hebben dezelfde hoogte
(met AD als basis) dus de oppervlakte van ADE is 36/10
keer zo groot als die van ABE ABE en ABC hebben dezelfde hoogte (met AC als basis) dus de oppervlakte van ABC is 24/15 keer zo groot als die van ABE De verhouding is dus 36/10 : 24/15 = 9 : 4 |
 |
|||
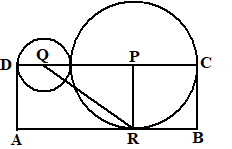
| 8. | Neem basis PR en hoogte PQ PQ is de helft van DC dus de oppervlakte van PQR is de helft van die van BCD Dus de oppervlakte is een kwart van de rechthoek, dus 31/4. |
|
|||
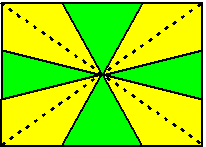
| 9. | Teken de diagonalen in de
rechthoek; die verdelen ede rechthoek in vier delen. In elk van die vier delen zie je twee gele en één groene driehoek die allemaal dezelfde oppervlakte hebben (namelijk dezelfde basis en hoogte) Dus geel : groen = 2 : 1 |
|
|||
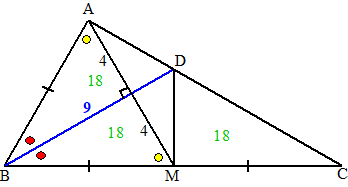
| 10. | Zie de figuur. De driehoeken BDA en BDM zijn congruent (ZZR) De oppervlakte van BDM is 0,5 9 4 = 18 De oppervlakte van BDA is ook 18 De oppervlakte van DMC is ook 18 (zelfde hoogte en zelfde basis als BMD) De totale oppervlakte is dus 54. |
 |
|||
| 11. | Zie de figuur hiernaast de rode
breuken geven aan hoeveelste deel het lijnstuk van de zijde van de
rechthoek is. driehoek ADM1: 1/2
1/2 1 = 1/4 |
|
|||
|
© h.hofstede (h.hofstede@hogeland.nl) |
|||||