|
||||||||
| 1. | ||||||||
|
|
||||||||
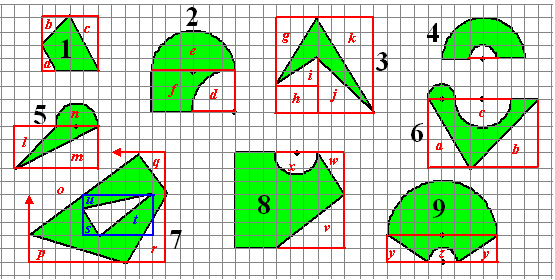
| 1.1. | hele oppervlakte is 4
• 3 = 12 a: 1 b: 2 c: 4 Dan blijft over 12 - 1 - 2 - 4 = 5 |
|||||||
| 1.2. | f + d
is samen 18. f is dan 18 - d = 18 - 1/4 • π 32 = 18 - 21/4π e is 1/2 • π • 32 = 41/2π Samen geeft dat 18 - 21/4π + 41/2π = 18 + 21/4π |
|||||||
| 1.3. | hele oppervlakte is
7 • 7 = 49 g : 71/2 h : 6 i : 3 j : 8 k : 14 Dan blijft over 49 - 71/2 - 6 - 3 - 8 - 14 = 101/2 |
|||||||
| 1.4. | grote halve cirkel:
1/2
•
π • 32 = 41/2π kleine halve cirkel: 1/2 • π • 12 = 1/2π Dan blijft over 41/2π - 1/2π = 4π |
|||||||
| 1.5. | rode rechthoek:
18 l : 41/2 m: 9 n: 1/2 • π • 22 = 2π Dat geeft samen 18 - 41/2 - 9 + 2π = 41/2 + 2π |
|||||||
| 1.6. | rode rechthoek:
40 a: 71/2 b: 121/2 c: 1/2 • π • 22 = 2π dat geeft 40 - 71/2 - 121/2 - 2π + 1/2 • π • 12 = 20 - 11/2π |
|||||||
| 1.7. | rode rechthoek :
80 o: 24 p: 7 q: 3 r: 7,5 blauwe rechthoek: 15 s: 1 t: 6 u: 21/2 het gat is dan 15 - 1 - 6 - 21/2 = 51/2 De oppervlakte is dan 80 - 24 - 7 - 3 - 71/2 - 51/2 = 33 |
|||||||
| 1.8. | hele rechthoek:
56 v: 10 w: 3 x: 1/2 • π • 11/22 = 9/8π dat geeft dan 56 - 10 - 3 - 9/8π = 43 - 9/8π |
|||||||
| 1.9. | rode rechthoek:
16 2 stukjes y: 2 • 3 = 6 z: 1/2 • π • 12 = 1/2π halve cirkel: 1/2 • π • 42 = 8π Dat geeft 16 + 8π - 6 - 1/2π = 10 + 71/2π |
|||||||
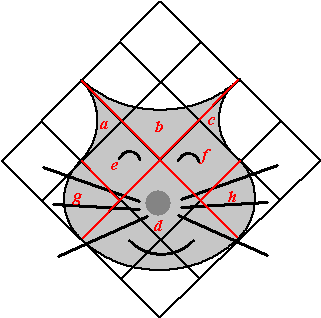
| 2. | a + c heel vierkant min een kwartcirkel 1 - 1/4 • π • 12 = 1 - 1/4π b: vierkant van 2 bij 2 min een kwartcirkel 4 - 1/4 • π • 22 = 4 - π e en f: oppervlakte 1 g en h: beiden een kwartcirkel: 1/4 • π • 12 = 1/4π d: kwartcirkel: 1/4 • π • 22 = π samen: 1 - 1/4π + 1 - 1/4π + 4 - π + 1 + 1 + 1/4π + 1/4π + π = 8 |
 |
||||||
| 3. | Trek lijnstukken
vanaf alle hoekpunten naar het midden. Een hoek in het midden is 40º tan 20º = 2/h geeft h = 5,49 voor de hoogte van een driehoek de oppervlakte van zo'n driehoek is dan 0,5 • 4 • 5,49 = 10,99 de hele negenhoek heeft dan oppervlakte 9 • 10,99 = 98,91 |
|||||||
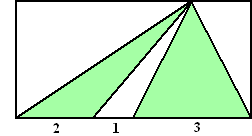
| 4. | de linker groene driehoek heeft
oppervlakte 1/2
• 2 • h de rechter groene driehoek heeft oppervlakte 1/2 • 3 • h samen is dat 2,5h de hele rechthoek heeft oppervlakte 6h dat is 2,5/6 • 100% = 42% |
|
||||||
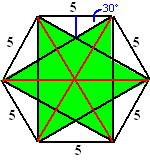
| 5. | De blauwe hoek is 30º Als het blauwe hoogtelijntje lengte h heeft, dan geldt: tan30º = h/2,5 h = 2,5 • tan30º = 2,5 • 1/3√3 De oppervlakte van de witte driehoek bovenaan is dan 1/2 • 5 • 21/2 • 1/3√3 = 25/12√3 De hele zeshoek bestaat uit 6 gelijkzijdige driehoeken met zijden 5 (zie de rode lijnen) Zo'n driehoek heeft hoogte H: H2 = 52 - 2,52 H = √18,75 De oppervlakte is dan 6 • 1/2 • 5 • √18,75 = 15√18,75 |
|
||||||
| Voor de ster blijft dan over: 15√18,75 - 6 • 25/12√3 = 43,30 | ||||||||
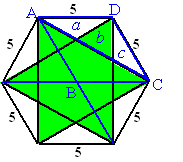
| Zie de figuur hiernaast. de ruit ABCD is 1/3 deel van de zeshoek. de driehoek ACD is de helft van de ruit, dus 1/6 deel van de zeshoek. De driehoekjes a, b. en c zijn even groot (zelfde basis en zelfde hoogte) dus elk is 1/18 deel van de zeshoek. Van de hele zeshoek gaan zes driehoekjes van 1/18 af, dus blijft over 1 - 6/18 = 1 - 1/3 = 2/3 deel. |
|
|||||||
| 6. | Zie de figuur
hiernaast. Daar staan allemaal 1-1-√2
driehoeken. In de linkerfiguur is de oppervlakte van het vierkant x2 en de oppervlakte van de driehoek 1/2 • 2x • 2x = 2x2 Het vierkant is de helft van de driehoek. In de rechterfiguur is de oppervlakte van het vierkant y2 en de oppervlakte van de driehoek 1/2 • (y√2 + y/√2)2 y/√2 = 1/2y√2, dus dat geeft voor de oppervlakte: 1/2 • (11/2y√2)2 = 1/2 • 21/4y2 • 2 = 21/4y2 Het vierkant is 1/2,25 = 4/9 deel van de driehoek. |
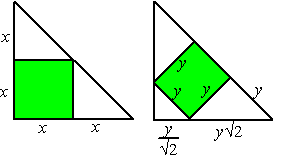 |
||||||
| De verhouding tussen beide manieren is 1/2 : 4/9 = 1 : 8/9 = 8 : 9 | ||||||||
| 7. |
|
|||||||
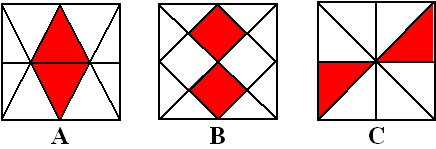
| A:
2/8
deel B: 2/8 deel C: 2/8 deel Het is allemaal 2/8 deel van het hele vierkant, dus de verhoudingen zijn 1 : 1 : 1 |
||||||||
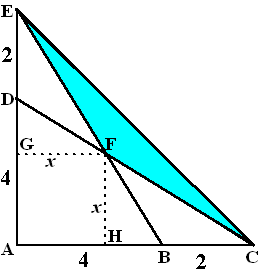
| 8. | Stel FH = FG = x Driehoeken BHF en BAE zijn gelijkvormig. |
|
||||||
|
||||||||
| Daaruit volgt
BH = 4 • x/6 Maar ook is BH = 4 - x (AB - GF) 2/3x = 4 - x 12/3x = 4 x = 2,4 |
||||||||
| Oppervlakte CBE =
1/2
• 2 • 6 = 6 Oppervlakte CBF = 1/2 • 2 • 2,4 = 2,4 Oppervlakte CFE = 6 - 2,4 = 3,6 |
||||||||
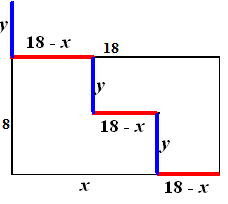
| 9. | Zie de figuur hiernaast. Die
gekleurde delen komen aan elkaar dus moeten even lang zijn. 3(18 - x) = 18 54 - 3x = 18 x = 12 2y = 8 y = 4 Het wordt bij herrangschikken inderdaad een vierkant van 12 bij 12. |
|
||||||
| OF (veel sneller): De oppervlakte van de rechthoek is 8 • 18 = 144 De oppervlakte van het vierkant dus ook, dus de zijden zijn 12. |
||||||||
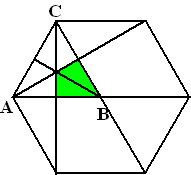
| 10. | Teken in de driehoek ABC alle
drie de hoogtelijnen. Je ziet dat het groene deel 1/3 van de driehoek is. Maar die driehoek is 1/6 van de zeshoek. Het groene deel is dus 1/3 • 1/6 = 1/18 van de zeshoek. Dat is 55/9% |
|
||||||
|
|
||||||||
|
© h.hofstede (h.hofstede@hogeland.nl) |
||||||||