© h.hofstede (h.hofstede@hogeland.nl)

       
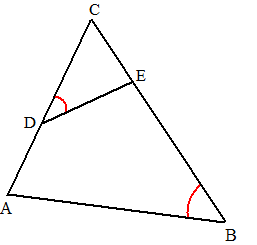
1. CDE ~ CAB

dus  CI/DF = CH/AB
(3 - x)/x = 3/4 
4(3 - x) = 3x
12 - 4x = 3x
12 = 7x
x = 12/7.
De oppervlakte is dan 144/49

       
2. ∠ACB = 30º
Dan is ∠CBA = 60º  dus ∠FBA = ∠FBE = 30º
De driehoeken AFB en EFB zijn gelijk

Stel dat de zijden van de eerste driehoek gelijk zijn aan x
Dan is dus EF = AF = 0,5x
Elke volgende driehoek is dus een verkleining van de vorige met factor 1/2.
De oppervlakte wordt dan vermenigvuldigd met 1/4
De vierde driehoek is dan  (1/4)3 van de eerste en dat is 1/64
De verhouding is dus 64 : 1

       
3. De vouw loopt door het  midden van BD en staat er loodrecht op.

BD = 100 (Pythagoras:  60-80-100)

DME ~ BAD

 
DM
50		 ME
?		 DE
 
BA
80		 AD
60		 BD
100
  ? = 50 • 60/80 = 37,5
De vouw is dan 2 • 37,5 = 75 cm lang.
       
4. Een rode en een groene hoek zijn steeds samen 90º.

DCE ~ BCF
 
BC
4		 CF
 		 BF
 
DC
8		 CE
 		 DE
 
     
  De oppervlakte van ECF is 25, dus  CE • CF = 50, dus  CE = 50/CF
Dan geeft de verhoudingstabel:  CF • 8 = 4 • 50/CF
Daaruit volgt  8CF2 = 200
CF2 = 25
CF = 5
Dan is CE = 10
102 = 82 + DE2
DE2 = 36
DE = 6
AE = 2
       
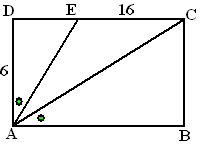
5. ADE  ~ ABC
Noem DE = x dan is  AB = 16 + x

 
AD
6		 DE
x		 AE
 
AB
16 + x		 BC
6		 AC
 
  x(16 + x) = 6 • 6
16x + x2 = 36
x2 + 16x - 36 = 0
(x - 2)(x + 18) = 0
x = 2  ∨  x = -18
x = 2 is de juiste oplossing.
De oppervlakte is dan  (2 + 16) • 6 = 108.
       
6. Zie de figuur hiernaast. Een rode en een groene hoek zijn samen 90º. Uit symmetrie volgt dat de beide rode hoeken bij M gelijk zijn.

ADM  ~ ABC
 
AD
x		 DM
4		 AM
 
AB
8		 BC
x		 AC
 
  32 = x2
x = √32
       
7. Hiernaast zie je het vooraanzicht van de tafel.
De rode stukken zijn afgezaagd.
De poten hadden oorspronkelijk lengte x

Als de tafel stabiel staat dan moet die schuine lijn een rechte lijn zijn.

     
  zie de afmetingen hiernaast.
 1/3x - 11 = 2 • 8   want de driehoeken hebben y en 2y als zijden, dus de hele driehoek is dubbel zo groot als de rechter.

Dat geeft  1/3x - 11 = 16
1/3x = 27
x =  81

       
8. AD2 = AM2 - MD2 = 252 - 52 = 600
AD = √600

ADM ~ ACB

 
AD
√600		 DM
5		 AM
25
AC
30		 CB
?		 AB
 
  ? = 5 • 30/√600 = 21/2√6
       
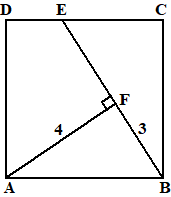
9. ABD ~ BCD ~ ACB
Stel CD = x dan is  AD = 4 - x

 
AB
 		 BD
1		 AD
4 - x
BC
 		 CD
x		 BD
1
AC
4		 CB
 		 AB
 
       
  1 • 1 = x(4 - x)
1 = 4x - x2
x2 - 4x + 1 = 0
x =  (4 ±√12)/2 = 2 ±√3
de juiste oplossing is  x = 2 - √3
Dan is  AD = 4 - x = 2 + √3
tanα = 1/(2 + √3)
α = 15º
       
10.

       
  ANC = DNC  dus  CD = 14 en DB = 5
ANM ~ ADB  met factor 2 want  AB = 2AM
Dan is NM = 1/2DB = 21/2
       
11. ∠ACD = ∠ABC want van beiden is de tangens gelijk aan x/2x = 1/2

Dan is  CAD ~ BAC en ∠ADC = 90º

 
CA
x		 AD
 		 CD
 
BA
 		 AC
x		 BC
2x
       
  BA = √(x2 + (2x)2) = √(5x2) = x√5
AD = x • x /x√5 = x/√5
CD = 2AD = 2x/√5
Oppervlakte van ADC is dan 1/2 • AD • CD = 1/2 • x/√5 • 2x/√5 = 1/5x2
Er zijn 8 zulke witte driehoeken in de figuur dus die hebben samen oppervlakte 8/5x2
Dan blijft voor de blauwe ster over:  (2x)2 - 8/5x2 = 2,4x2
Als de zijde van het vierkant z = 2x is, dan is x = 1/2z en de oppervlakte is 2,4 • (1/2z)2 = 3/5z2 
       
12. Zie de figuur hiernaast.
vanwege het raken is ∠ACM = 90º
Een rode en een groene hoek zijn samen 90º

MBC ~ ABM

 
MB
4		 BC
 		 MC
 
AB
5		 BM
4		 AM
3
       
  straal is MC =  4 • 3/5 = 2,4
       
13. AEH ~ CAB ~ GEI

 
AE
 		 EH
 		 AH
1
CA
5		 AB
4		 CB
3
GE
 		 EI
12/3		 GI
 
       
  EH = 1 • 4/3 = 4/3  dan is  EF = 22/3  en  EI = 12/3
GI = 3 • EI/4 = 5/4
De groene oppervlakte is  1/2 • 12/3 • 5/4 = 25/24
       
14.
DC
x		 CA
6		 DA
 
DA
 		 AB
8		 DB
7 + x
       
  Stel DC = x dan is  DB = 7 + x
DA = 8x/6  en ook  DA = 6 • (7 + x)/8
dus  8x/6 = 6(7 + x)/8
64x = 36(7 + x)
28x = 252
x = 9 = DC
       
15. MBP ~ NAP
Stel NP = x dan is  MP = x + R + r

 
MB
R		 BP
8		 MP
x + R + r
NA
r		 AP
4		 NP
x
     
  8R = 4r dus R = 2r
8x = 4(x + 3r)
Dat geeft  x = 3r
Pythagoras in NAP:  r2 + 42 = (3r)2
  r2 + 16 = 9r2
r2 = 16/8 = 2
r = √2
       
16. Zie de figuur hiernaast. Een rode en een blauwe hoek zijn samen 90º

Dan is ∠DEN = 90º en  DEN ~ CDN
CN = √(602 + 302) = √4500

 
DE
 		 EN
 		 DN
30
CD
60		 DN
30		 CN
W4500
       
  DE = 30 • 60/√4500 = 1800/√4500
EN = 30 • 30/√4500 = 900/√4500
oppervlakte DEN = 1/2 • 1800/√4500 • 900/√4500 = 180

Verder is AFM ~ DFC (zandloper) met factor 2.
Dus de hoogte van AFM is 1/3 van het vierkant, dus 20
Oppervlakte AFM = 1/2 • 30 • 20 = 300

opp(NEFA) = opp(AMD) - opp(AFM) - opp(DNE)
= 900 - 300 - 180 = 420
       
17. CDM  ~ CAB ~  MEB
CB = √42 (Pythagoras in ABC)

 
CD
 		 DM
r		 CM
 
CA
6		 AB
4		 CB
√42
ME
r		 EB
 		 MB
 
     
  CM = r • √42/4
MB = r •√42/6
CM + MB = BC geeft dan  r • √42/4 + r • √42/6 = √42
5/12r√42 = √42
r = 12/5
       
18 Teken een lijn van D loodrecht op BC.
Een rode en een groene hoek zijn samen 90º
Dus is ∠BDE twee roden = ∠ACB

ABC ~  EBD en  ADC = EDC  (precies hetzelfde)
Dan is  EB = 3 (Pythagoras)

 
AB
9		 BC
 		 AC
 
EB
3		 BD
5		 ED
4
     
  AC = 9 • 4/3 = 12
oppervlakte ABC = 1/2 • 12 • 9 = 54
       
19. Uit twee gelijkvormige driehoeken zien we dat
H/(x + 1) = h/x  ofwel H = h • (x + 1)/x = h(1 + 1/x)

Elke groene driehoek hiernaast is 1/6 van de hele driehoek. (immers de drie samen zijn de helft)
1/6 • 1/2 • (x + 1) • H = 1/2 • 1 • h

substitutie geeft  1/12 • (x + 1) • (1 + 1/x) • h = 1/2 • h
⇒ x + 2 + 1/x = 6
⇒ x2 - 4x + 1 = 0
⇒ (ABC):    x = 2 + √3   (de oplossing x = 2 - √3 valt af want x > 1)

       
20. ABF ~ ECF

 
AB
6		 BF
8		 AF
10
EC
 		 CF
 		 EF
3
     
  EC = 6 • 3/10 = 1,8  dus  DE = 6 - 1,8 = 4,2
CF = 8 • 3/10 = 2,4 dus  AD = 8 - 2,4 = 5,6
oppervlakte ADE is  1/2 • 4,2 • 5,6 = 11,76
       
21. Zie de figuur hiernaast.
een rode en een groene hoek zijn steeds samen 90º

CDE ~ EDA ~ AEB ~ CEA ~ CAB

Noem EB = x dan is  CE = 169 - x

 
AE
60		 EB
x		 AB
 
CE
169-x		 EA
60		 CA
 
     
  x(169 - x) = 3600
169x - x2 = 3600
x2 - 169x + 3600 = 0
x = 25 ∨  x = 144
De juiste oplossing is x = EB = 25 (EB < EC) en dan is  CE = 144
AB = √(602 + 252) = 65
       
 
CD
 		 DE
 		 CE
144
AE
60		 EB
25		 AB
65
 
       
  CD = 144 • 60/65 = 1728/13  ( ≈133)
       
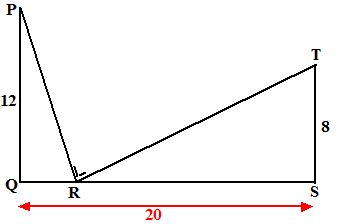
22. PQR ~ RST
Stel QR = x dan is  RS = 20 - x

     
 
PQ
12		 QR
x		 PR
 
RS
20 - x 		ST
8		 RT
 
     
  x(20 - x) = 8 • 12
20x - x2 = 96
x2 - 20x + 96 = 0
(x - 12)(x - 8) = 0
x = 12 ∨ x = 8
De juiste is x = 8  en dan is QR = 8 en RS = 12
       
23. Zie de figuur hiernaast.
Kies de afmeting x, dan volgen de andere afmetingen uit het feit dat dit een 3-4-5 driehoek is (er zijn steeds twee driehoeken met gemeenschappelijke rode schuine zijde gelijk aan elkaar)

r = 4 - x  en  r = x - 2  geeft  4 - x = x - 2  dus  x = 3
Dan is r = 1

       
24. BC = AB = √2 (vanwege de gelijkvormigheid.
Stel de straal van de cirkel r
MQ staat loodrecht op BC en op AB, dus is  BQ = r
Dan is CQ = BC - BQ = √2 - r

Driehoeken MQC en MPC zijn congruent (ze hebben twee zijden en een hoek gelijk)
Dus is PC = CQ = √2 - r

AD = 2 (Pythagoras in ABC) dus DC = 1 
dus PD = 1 + √2 - r

 

AR =  √2 + r  = AP (want ook AMP en AMR zijn gelijkvormig)
dus √2 + r = 2 + √2 - r ⇒  r = 1

Dus PD = √2 en MP = 1
Pythagoras in MPD geeft dan  MD2 = 2 + 1 = 3  ⇒  MD = √3

       
25. Neem zijden van 5 (de lengte doet er niet toe)

AE2 + 2,52 = 52  geeft  AE = √18,75
BCD is gelijkvormig met ACF met factor 0,2
Dus BD = 0,2 • AF = 0,2√18,75
EC = 4
oppervlakte van ECD = 0,5 • 4 • 0,2√18,75
= 0,4√18,75

De hele driehoek heeft oppervlakte 0,5 • 5 • √18,75
= 2,5√18,75

Om de rode driehoek te krijgen gaan daar drie van die driehoeken als ECD van af.

       
  De rode driehoek heeft oppervlakte 2,5√18,75 - 3 • 0,4√18,75 = 1,3√18,75
De verhouding is dan  1,3 : 2,5
       
26. a. CDE is gelijkvormig met CBA (beiden hoek C en de rode hoek)

CD/CE = CB/CA
CD/2 = 6/4
CD = 3

       
  b. DE = x  en dus AB = x + 2
DE/CD = BA/BC
x/3 = (x + 2)/6
6x = 3(x + 2)
6x = 3x + 6
3,x = 6
x = 2
 		  
       
27. Zie de figuur.
DESD  ~ DEDA 
ES/ED = ED/EA
ES/4 = 4/√48
ES = 16/√48

SD/ED = DA/EA
SD/4 = 8/√48
SD = 32/√48

De oppervlakte is dan 1/2 • 16/√48 • 32/√48 = 51/3

       
28. zandloperfiguur, dus gelijkvormige driehoeken.

x + y = 90  dus  x = 90 - y

verhoudingen:   x/60 = y/25
dus 25x = 60y
25(90 - y) = 60y
2250 - 25y = 60y
85y = 2250
y = 26,47
Dan is x = 63,53

       
29. Gelijkgekleurde hoeken hiernaast zijn gelijk (allemaal paren Z-hoeken)

DPN ~ BPC  (zandloper)
omdat BC = 2PN  is ook BP = 2DP dus DP is 1/3 deel van BD.

MQB ~  CQD (zandloper)
omdat DC = 2MB is ook DQ = 2BQ dus is BQ 1/3 deel van BD. 

       
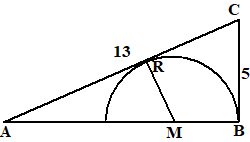
30. AB = √(132 - 52) = 12
Noem de straal r
ABC  is gelijkvormig met ARM

MB = r dus AM = 12 - r
 
AB
12		 BC
5		 AC
13
AR RM
r		 AM
12 - r

5(12 - r) = 13r
60 - 5r = 13r
60 = 18r
r = 31/3

       
31.

       
  Zie de figuur
x2 + 42 = (16 - x)2
x2 + 16 = 256 - 32x + x2
32x = 240
x = 7,5
Maar de blauwe hoeken zijn gelijk (beiden met HMAN 90º) dus de driehoeken ABN en AD'M zijn gelijk
Dan is AM = AN = 16 - 7,5 = 8,5
Dan is ABNM precies de helft van  ABCD  (NCDM is de andere helft)
ABNM heeft dus oppervlakte 32.
 AMD' heeft oppervlakte 0,5 • 4 • 7,5 = 15
De vijfhoek heeft oppervlakte 15 + 32 = 47
       
32. De gele driehoeken zijn gelijkvormig met factor 2.
Dus lijnstuk a is 1/3 van de diagonaal.
Lijnstuk b is 1/2 van de diagonaal

Dan blijft er voor het rode deel 1 - 1/3 - 1/2 = 1/6 deel over.

       
33. Teken het lijnstuk MR (zie de figuur)

De groene driehoeken zijn congruent (DP = MR)
De rode driehoeken zijn congruent (QB = MR)

De oppervlakte van MQCP is dus gelijk aan de oppervlakte van BCD en dus 18.

       
34. AB = 5   (pythagoras)
BC = 5  (vierkant)

ABF is gelijkvormig met EBC met factor 5/4
Dus EC = 5/4 • 3 = 3,5

ED = 1,5

       
35. De driehoeken CQB en  ABP zijn gelijkvormig met factor 2.
Stel CB = x, dan is AP = 2x
Stel CQ = y dan is AB = 2y dus DQ = 2y - x

Pythagoras in driehoek PQD:

PQ2 = (2x + y)2 + (2y - x)2
= 4x2 + 4xy + y2 + 4y2 - 4xy + x2  
= 5x2 + 5y2
= 5(x2 + y2)
= 5 • 82
= 320
Dus PQ = √320 = 8√5   

       
36. Vanwege de gelijke basishoeken zijn de driehoeken KOE en OBE gelijkvormig.

Dus  2/2a = a/2

Dat geeft 2a2 = 4  dus  a = √2
De hoogte h is dan  √((2a)2 - 12) = √7

De oppervlakte is dan  0,5 • 2 • √7 = √7

       
37.

       
  Zie de figuur met de afmetingen op de x-as.
QRA en QCO zijn gelijkvormig, dus  AR/(1/p - 1) = 1/(1/p) 
Dat geeft AR • 1/p = 1/p - 1  dus  AR = 1 - p
AR = PA dus de driehoeken ACR en ACP zijn congruent.
Dus de hoeken RCA en PCA zijn geljk en dat zijn precies de gevraagde hoeken.
       

© h.hofstede (h.hofstede@hogeland.nl)