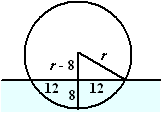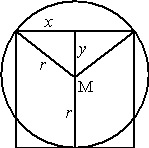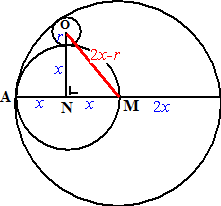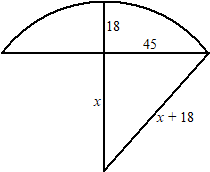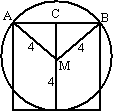
© h.hofstede (h.hofstede@hogeland.nl)

       
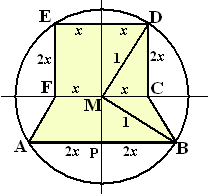
1. zie wat afmetingen hiernaast.

driehoek MCD:   2x2 + x2 = 12
3x2 = 1
x2 = 1/3
x = 1/3√3

MCD heeft oppervlakte  0,5 • x• 2x = 1/3
MPB is dezelfde driehoek, dus heeft ook oppervlakte 1/3, en dus is ook MP = x
MCB heeft oppervlakte  0,5 • x • x = 1/6

De hele figuur heeft dan oppervlakte  6 • 1/3 + 2 • 1/6 = 21/3.  
       
2.

       
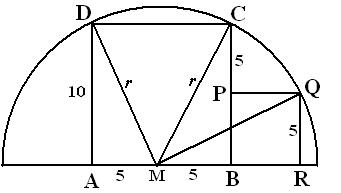
  in driehoek AMD:   52 + 102 = r2  ⇒  r2 = 125
Als BC = 10 dan is  QR = PB = 5
in driehoek MQR:   MR2 + 52 = r2 = 125
Dus MR = 10
Dan is  BR = 5
De oppervlakte van BPQR is dan 25.
       
3. zie de figuur hiernaast.

(r - 5)2 + (r - 10)2 = r2 
r2 - 10r + 25 + r2 - 20r + 100 = r2
r2 - 30r + 125 = 0
(r - 5)(r - 25) = 0
r = 5  ∨  r = 25
De gezochte oplossing is r = 25
       
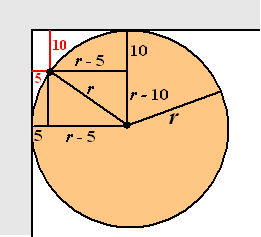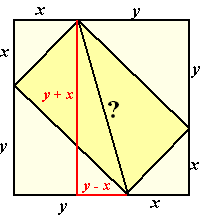
4. Noem de afmetingen van de driehoeken x en y zoals hiernaast.

Oppervlakte is dan x2 + y2 = 200

Diagonaal:  L2 = (x + y)2 + (y - x)2
L2 = x2 + 2xy + y2 + y2 - 2xy + x2
L2 = 2(x2 + y2) = 2 • 200 = 400
L = √400 = 20

       
5. zie de figuur hiernaast.
r2 = 122 + (r - 8)2
r2 = 144 + r2 - 16r + 64
16r = 208
r = 208/16 = 13

       
6.

       
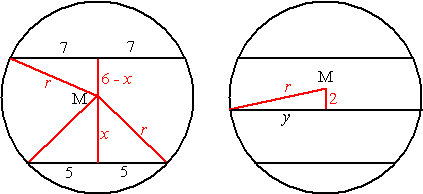
  linkerfiguur: 
r2 = 72 + (6 - x)2  dus  r2 = 85 - 12x + x2
r2 = x2 + 52  dus  r2 = x2 + 25
gelijkstellen geeft dan  12x = 60 ⇒ x = 5 ⇒ r = √50

rechterfiguur:  als x = 5 dan is de afstand van M tot de lijn in het midden gelijk aan 2.
r2 = 22 + y2
50 = 4 + y2
y2 = 46
y = √46
De lengte van de lijn in het midden is dan 2√46
       
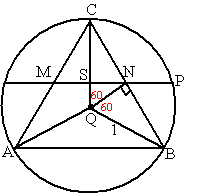
7. Hoek BQC is 120º
Omdat N het midden van BC is, is QN de hoogtelijn van driehoek QCB
Dus hoek BQN en CQN zijn beiden 60º

in driehoek BQN:  cos60º = QN/BQ  dus  QN = BQ • cos60º = 1/2
in driehoek QSN:  cos60º = QS/QN dus QS = QN • cos60º = 1/4

in driehoek QSP:   12 = (1/4)2 + SP2 
1 = 1/16 + SP2
SP2 = 15/16
SP = 1/4√15 
 

  in driehoek QNC:  tan60º = CN/QN  dus  CN = QN • tan60º = 1/2 • √3
Dan is AB = W3 en dus  MN = 1/2√3  dus  SN = 1/4√3

NP = SP - SN = 1/4√15 - 1/4√3
       
8.

       
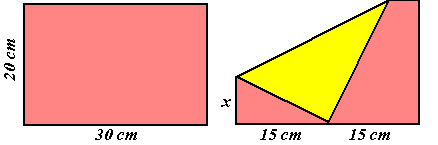
  rechterfiguur:  in de driehoek linksonder is de schuine zijde gelijk aan 20 - x
x2 + 152 = (20 - x)2
x2 + 225 = 400 - 40x + x2
40x = 175
x = 43/8 cm en dat is ongeveer 44 mm
       
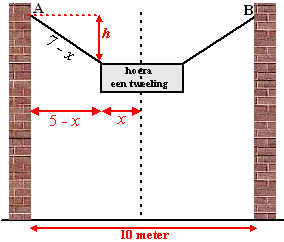
9. Noem de lengte van het halve spandoek x
Dan zijn de afmetingen zoals in de figuur hiernaast.

(5 - x)2 + 42 = (7 - x)2
25 - 10x + x2 + 16 = 49 - 14x + x2
4x = 8
x = 2
Het spandoek is 4 meter lang.
       
10. Zie de afmetingen hiernaast.
Stel dat het vierkant zijden 2x heeft en de cirkel straal r.
Dan geldt  y = 2x - r

y2 + x2 = r2
(2x - r)2 + x2 = r2
4x2 - 4xr + r2 + x2 = r2
5x2 = 4xr
x = 0,8r

       
  De oppervlakte van het vierkant is  4x2 = 4(0,8r)2 = 4 • 0,64r2 = 2,56r2
De oppervlakte van de cirkel is πr2
De verhouding is dan  π : 2,56   (ongeveer  1 : 0,81)
       
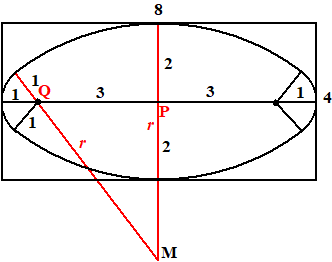
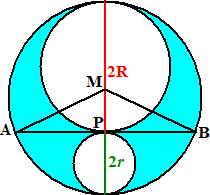
11. Noem de straal van de grote cirkel 2x
Dan heeft de cirkel met middelpunt N straal x
Noem de straal van de kleine cirkel r

Als je de lijn MO doortrekt naar de rand van de grote cirkel, dan heeft dat lijnstuk totale lengte 2x.
Dus is  MO = 2x - r

Omtrek driehoek MNO:  x + (x + r) + (2x - r) = 8
4x = 8
x = 2

In driehoek MNO:
x2 + (x + r)2 = (2x - r)2
4 + 4 + 4r + r2 = 16 - 8r + r2
12r  = 8
r = 2/3

       
12. zie de figuur hiernaast.

noem de zijde van het vierkant x
dan is MC = x - 4 en  AC = 1/2x
Pythagoras in driehoek AMC:
42 = (1/2x)2 + (x - 4)2
16 = 1/4x2 + x2 - 8x + 16
0 = 11/4x2 - 8x
0 = x(11/4x - 8)
x = 0  ∨   x = 6,4
Als x = 6,4 dan is de oppervlakte gelijk aan 40,96

       
13. Noem de rechthoekszijden a en b
Dan is  a2 + b2 = 252  en  1/2ab = 84
a = 168/b  geeft  (168/b)2 + b2 = 625
28224 + b4 = 625b2
b4 - 625b2 + 28224 = 0
b2 = 576 ∨ b2 = 49
Dat geeft b = 24  ∨  b = 7
Dan is a = 7  of  a = 24
De rechthoekszijden zijn dus 24 en 7 en de omtrek is 7 + 24 + 25 = 56
       
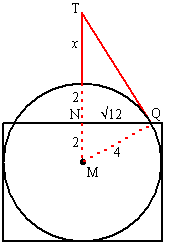
14. a. Zie het vooraanzicht hiernaast.

NP2 = MP2 - MN2 = 42 - 22 = 12  dus  NP = √12

De oppervlakte van de snijcirkel is dan
π•(√12)2 = 12π

Het hele vlak heeft oppervlakte 8 • 8 = 64
Het vlakke gedeelte is dan 64 - 12π = 26,3

       
  b. Zie het vooraanzicht hiernaast.
De top T van de mast is overal te zien als hij te zien is vanaf punt Q op de snijcirkel van de bol met het bovenvlak.

Kijklijn  QT is raaklijn aan de bol dus QT staat loodrecht op MQ.

Noem de masthoogte x, dan geldt;

(x + 2)2 + (√12)2 = QT2   in driehoek NQT
(x + 4)2 - 42 = QT2  in driehoek MQT

dus geldt  (x + 2)2 + (√12)2  = (x + 4)2 - 42
x2 + 4x + 4 + 12 = x2 + 8x + 16 - 16
16 = 4x
x = 4
De minimale hoogte van de mast is 4.

       
15. Noem de rechthoekszijden a en b en de schuine zijde c = p + q
De hoogtelijn verdeelt de driehoek in twee kleinere driehoeken.
Pythagoras in die driehoeken:
h2 + p2 = a2
h2 + q2 = b2
Optellen:   2h2 + p2 + q2 = a2 + b2  =  c2
Maar c = p + q
Dus  2h2 + p2 + q2 = (p + q)2  = p2 + 2pq + q2
2h2 = 2pq
h2 = pq
       
16. Als AB door het middelpunt gaat, dan moet hoek ACB een rechte hoek zijn, dus moet Pythagoras gelden:

142 + 482 = 196 + 2304 = 2500
Dat is inderdaad precies gelijk aan  AB2 = 502

AB gaat dus WEL door het middelpunt van de cirkel.
       
17. Stel de x-coördinaat van M3 is gelijk aan  p  en de straal van c3 is r
Pythagoras in M1PM3:    (p - 2)2 +  r2 = (r + 2)2  
p2 - 4p + 4 + r2 = r2 + 4r + 4
p2 - 4p = 4r    ....(1)

Pythagoras in M2PM3:   (p + 6)2 + r2 = (r + 6)2
p2 + 12p + 36 + r2 = r2 + 12r + 36
p2 + 12p = 12r   ....(2)

(1) invullen in (2):  p2 + 12p = 3p2 - 12p
2p2 - 24p = 0
2p(p - 12) = 0
p = 0  ∨  p = 12
De gezochte oplossing is p  = 12
Dan is  4r = 122 - 4 • 12 = 96  dus  r = 24.
       
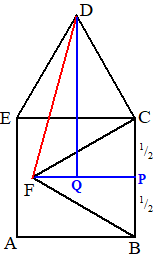
18. FP2 + 1/22 = 12  dus  FP = 1/2√3
FQ = FP - QP = FP - 1/2 = 1/2√3 - 1/2
DQ = 1/2√3 + 1/2

FD2  = (1/2√3 - 1/2)2 + (1/2√3 + 1/2)2
FD2  =  3/4 - 1/2√3 + 1/4 + 3/4 + 1/2√3 + 1/4 = 2

FD = √2

       
19.

       
  MP = r - 2
PQ = 3
MQ = r - 1
(r - 2)2 + 32 = (r - 1)2
r2 - 4r + 4 + 9 = r2 - 2r + 1
12 = 2r
r = 6
       
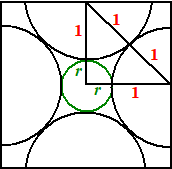
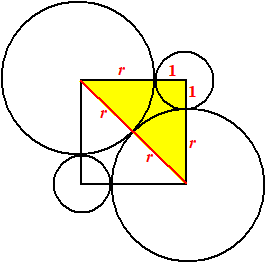
20. Pythagoras in de gele driehoek:

(2r)2 = (r + 1)2 + (r + 1)2
4r2 = 2r2 + 4r + 2
r2 - 2r - 1 = 0
r = (2 ± √8)/2
r = 1 + √2

OF:
De driehoek is een 1-1-√2  driehoek dus 2r = (r + 1)√2
daaruit volgt hetzelfde.
       
21. Noem de straal van de grote witte cirkel R en die van de kleine witte cirkel r
Dan is de straal van de grote cirkel R + r.

De oppervlakte van de grote cirkel is  π(R + r)2 = π(R2 + 2rR + r2)
Blauwe deel heeft dan oppervlakte:
 π(R2 + 2rR + r2) - πR2 - πr2 = π2rR = 2π
Daaruit volgt dat Rr = 1

Noem het middelpunt van de grote cirkel M
Dan is MP hiernaast R + r - 2r = R - r
Pythagoras in MAP:
(R + r)2 = AP2 + (R - r)2
R2 + 2Rr + r2 = AP2 + R2 - 2rR + r2
AP2 = 4rR
Maar omdat Rr = 1 is  AP2 = 4  dus AP = 2
AB  is dan gelijk, aan 4.

       
22. Zie de figuur hiernaast.

22 = (1 + r)2 + (1 + r)2
4 = 2 + 4r + 2r2
r2 + 2r - 1 = 0
r = (-2 ± √(4 + 4))/2  = -1 + √2

       
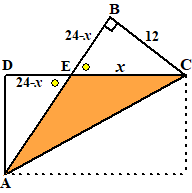
23. Neem de middelste figuur.
De driehoeken ADE en CBE zijn gelijk.

Pythagoras:  (24 - x)2 + 122 = x2
576 - 48x + x2 + 144 = x2
48x  = 720
x = 15

 

       
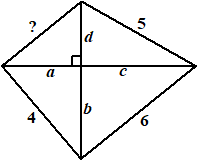
24. a2 + b2 = 42   dus  b2 = 16 - a2
b2 + c2 = 62  dus  16 - a2 + c2 = 36  dus  c2 = 20 + a2
d2 + c2 = 25  dus  d2 + 20 + a2 = 25  dus  d2 = 5 - a2

a2 + d2 = a2 + 5 - a2 = 5

De vierde zijde is dus √5

       
25. Zie de figuur waarin P de projectie van M op de x-as is.
NP = OP - ON = 14 - r

Pythagoras in driehoek MPN:   (10 + r)2 = (14 - r)2 + 64
100 + 20r + r2 = 196 - 28r + r2 + 64
48r = 160
r = 31/3
       
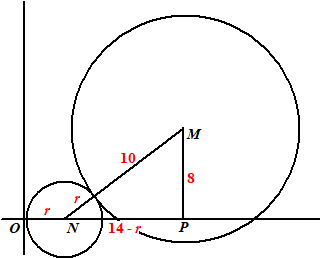26. Zie het schetsje hiernaast.

x2 + 452 = (x + 18)2
x2 + 2025 = x2 + 36x + 324
36x = 1701
x = 47,25
r = 47,25 + 18 = 65,25 ≈ 65 cm.

       
27. Je moet aantonen dat a2 + c2 = b2 + d2

a2 = g2 + f2
c2 = h2 + e2
b2 = f2 + h2
d2 = g2 + e2

dus a2 + c2 = g2 + f2 + h2 + e2
en  b2 + d2 = f2 + h2 + g2 + e2
Dat is inderdaad gelijk.

       
28.      
       

© h.hofstede (h.hofstede@hogeland.nl)