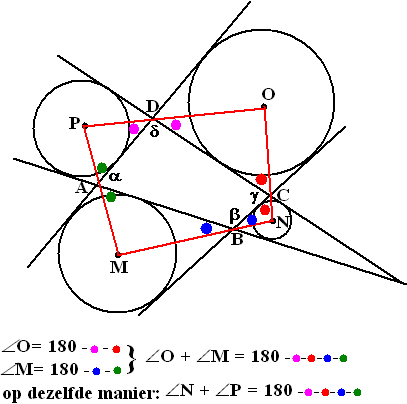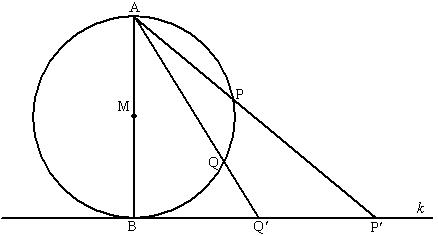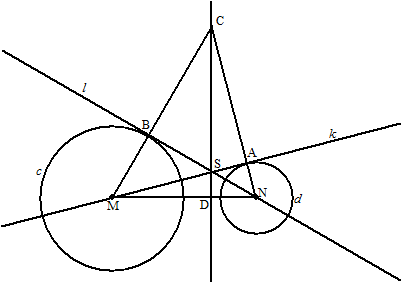|
|||||
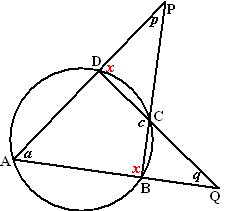
| 1. | Hiernaast zie je
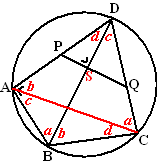
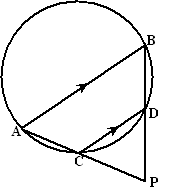
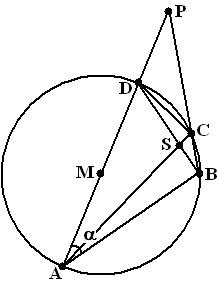
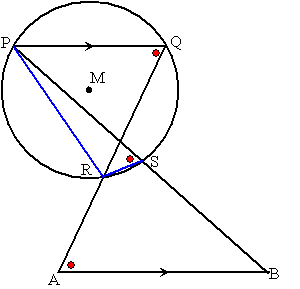
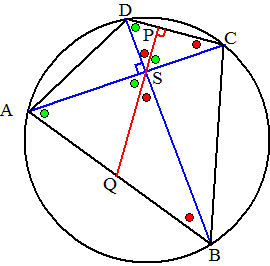
gelijke letters in gelijke hoeken, allemaal vanwege omtrekshoeken a van koorde AD, b van koorde DC, c van koorde BC en d van koorde AB. Vanwege Thales is ∠DAB = 90º (DB is een middellijn) De driehoeken DSP en DAB zijn gelijkvormig, dus is ∠DPS = a ∠PQC = c + d + a (buitenhoek driehoek PDQ) Dan is ∠PQC + ∠PAC = a + b + c + d Dat is 180º omdat dat gelijk is aan ∠ABC + ∠ADC en ABCD was een koordenvierhoek. omdat ∠PQC + ∠PAC = 180º is PACQ een koordenvierhoek. |
|
|||
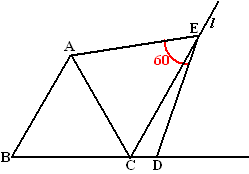
| 2. | a. | l evenwijdig aan AB dus
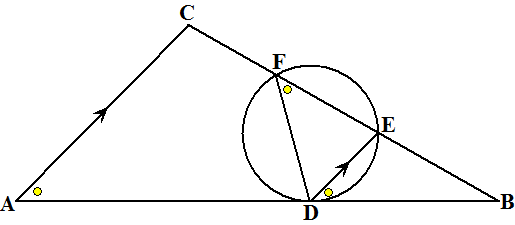
∠ECD = 60º (F-hoeken) ∠BCA = 60 º (gelijkzijdige driehoek) Dus is ook ∠ACE = 60º (rechte lijn BCD). ∠AED + ∠ACD = 60 + 120 = 180º dus is ACDE een koordenvierhoek. |
|
||
| b. | Het is beiden de omtrekshoek van koorde CD (van de cirkel door ACDE). | ||||
| c. | ∠ADE
= ∠ACE = 60º (beiden omtrekshoek van AE, dat ∠ACE 60º is, staat in vraag a) Dus zijn alle hoeken van driehoek ADE 60º, dus is de driehoek gelijkzijdig. |
||||
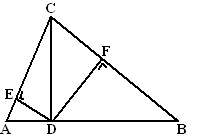
| 3. | ∠CED
= 90º en ∠DFC = 90º Dus zijn ze samen 180º en dus is CEDF een koordenvierhoek.
∠CDE = ∠CFE
(beiden omtrekshoek van koorde CE) |
|
|||
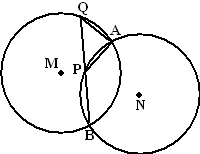
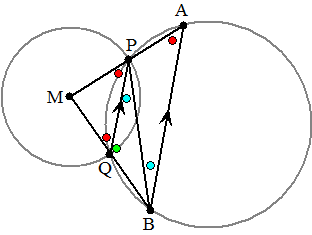
| 4. | Kies (de kleinste)
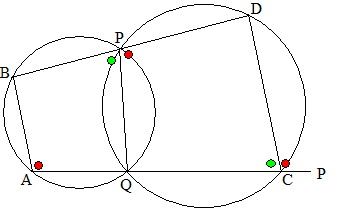
koorde AB van de linkercirkel Daarvan is de middelpuntshoek ∠AMB = 2α De omtrekshoek van die koorde is dan α, en dat is ∠AQP. In de rechtercirkel heeft de (kleinste) koorde AB dan ook omtrekshoek α (de cirkels zijn even groot) Dan heeft de grootste koorde AB in die cirkel omtrekshoek 180 - α, en dat is gelijk aan ∠APB Als ∠APB = 180 - α, dan is ∠APQ = α Dus ∠APQ = ∠AQP dus is driehoek APQ gelijkbenig en dus is AQ = AP. |
|
|||
| 5. | a. | ∠DAB + ∠DCB = 180º (koordenvierhoek ∠DCB + ∠PCB = 180º (rechte lijn) dus ∠DAB = ∠PCB ∠ADC + ∠ABC = 180º (koordenvierhoek) ∠ABC + ∠PBC = 180º (rechte lijn) dus ∠ADC = ∠PBC |
|
||
| Dan is driehoek PAD
gelijkvormig met driehoek PCB Dus PA/PD = PC/PB PA PB = PC PD |
|||||
| b. | Omdat ABCD een
willekeurige koordenvierhoek was, mag je C en D ook wel ergens anders
kiezen. Trek de lijn van P door M, en kies als C en D de snijpunten van die lijn met de cirkel. Dan is PC = PM - r en PD = PM + r PA PB = PC PD = (PM - r)(PM + r) = PM2 - r2 |
||||
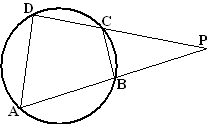
| 6. | Noem
∠PDC = x Dan is ∠ADC = 180 - x (rechte lijn) Dan is ∠ABC = x (koordenvierhoek: samen 180º) c is de buitenhoek van driehoek BQC dus c = q +
180 - x |
|
|||
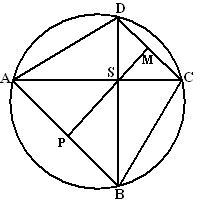
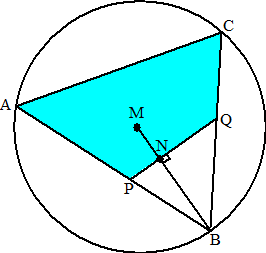
| 7. | M is het midden van
DC, en ∠DSC = 90º Dus is er een cirkel door D, S en C met middellijn DC (Thales) Dan is MS = MD = MC, dus is driehoek SMC gelijkbenig, en zijn de hoeken MCS en MSC gelijk (basishoeken) ∠ASP = ∠MSC (overstaande hoeken) dus ∠ASP = ∠MCS ∠PAS = ∠SDC (beiden omtrekshoek van koorde BC) Dus zijn de driehoeken APS en DSC gelijkvormig en is ∠APS = 90º |
|
|||
| 8. | Als DC middelloodlijn
is, dan is DC de verzameling van alle punten die even ver van A als van
B afliggen. Dus ligt het middelpunt van de cirkel ook op DC, dus DC is een middellijn van de cirkel. Dan is ∠DQC = 90º (Thales) ∠DMP = 90º vanwege de middelloodlijn Dus is ∠DMP + ∠DQC = 180º dus is MPQD een koordenvierhoek. |
|
|||
| 9. | a. | Stel ∠PDC
= x Dan is ∠PBA = x (F-hoeken) Dan is ∠ACD = 180 - x (koordenvierhoek) Dan is ∠PCD = x (rechte lijn) Dus is driehoek PDC gelijkbenig en is PC = PD. |
|
||
| b. | Als ∠PDC
= ∠PCD (zie vraag a) dan is ook ∠PAB = ∠PBA (F-hoeken) Dus is driehoek PBA gelijkbenig, en is PB = PA AC = PA - PC = PB - PD = BD |
||||
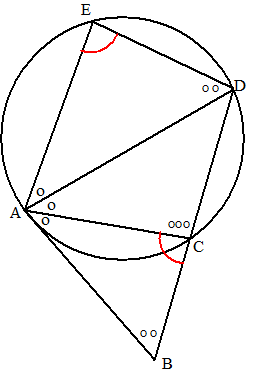
| 10. | ∠B
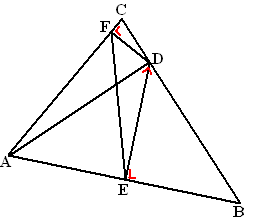
+ ∠EDB = 90º ∠ADE + ∠EDB = 90º Dus is ∠ADE = ∠B ∠C + ∠CDF = 90º ∠CDF + ∠FDA = 90º Dus is ∠C = ∠FDA ∠C + ∠B + ∠A = 180º dus ∠C + ∠ADE + ∠FDA = 180º en dat is ∠C + ∠FDE Dus is AFDE een koordenvierhoek. Als AFDE op één cirkel liggen is ∠ADE = ∠AFE (beiden omtrekshoek van koorde AE Dus is ook ∠B = ∠AFE. |
|
|||
| 11. | Omdat
∠AFE = ∠AEB = 90º
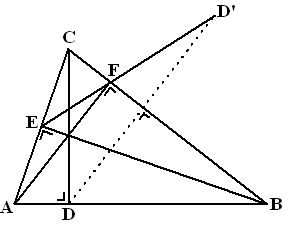
is AB de middellijn van een cirkel door A, B, F en E (Thales) Dus is ABFE een koordenvierhoek. ∠BAE + ∠BFE = 180º (koordenvierhoek) ∠CFE + ∠BFE = 180º (rechte lijn Dus is ∠CFE = ∠BAE. Doe hetzelfde nu met AC: ∠ADC = ∠AFC = 90º dus is AC een middellijn van een cirkel door A, D, F, C. ∠BAC + ∠DFC = 180º (koordenvierhoek) ∠DFC + ∠DFB = 180º (rechte lijn) Dus ∠DFB = ∠BAC Dus ∠DFB = ∠CFE (beiden gelijk aan ∠BAC) Vanwege het spiegelen is ook ∠D'FB = ∠DFB Dus is ∠D'FB = ∠CFE. Het zijn kennelijk overstaande hoeken, dus is ED' een rechte lijn. |
|
|||
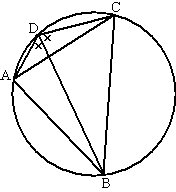
| 12. | hoek BCA
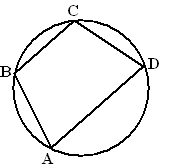
= hoek DAC (Z - hoeken) Het zijn de omtrekshoeken van bgBA en bg CD, dus bg BA = bg CD Dus BA = CD en dat zijn twee even lange overstaande zijden. |
|
|||
| 13. | a. | M ligt even ver van BA als van BC
dus is MB bissectrice van de hoek bij B. Op dezelfde manier is BN ook bissectrice van de hoek bij B. Omdat de hoeken overstaande hoeken zijn, zijn ze gelijk. Dus ∠MBA + ∠ABC + ∠CBN = ∠MBA + ∠ABC + ∠MBA = 2∠MBA + ∠ABC = 180º Dus is MBN een rechte lijn. |
|||
| b. | Vanwege de
bissectrices (zie vraag a) zijn de gekleurde hoeken hieronder even
groot. Onder de figuur wordt bewezen dat ∠O + ∠M = ∠N + ∠P Omdat de vier hoeken van een vierhoek samen 360º zijn, zijn beide koppels dus gelijk aan 180º. Maar dan is MNOP een koordenvierhoek, dus liggen de vierhoekpunten op één cirkel. |
||||
|
|
|||||
| 14. |
|
||||
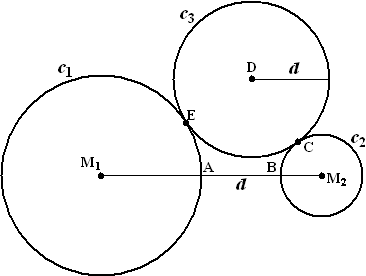
| a. | Driehoek
M1EA is gelijkbenig, want M1E = M1A = r1.
Dus is ∠M1EA = ∠M1AE. Maar dan is ∠DEA = 180º - ∠M1EA = 180º - ∠M1AE = ∠BAE. Noem deze hoeken α. Driehoek M1DB is ook gelijkbenig,
want M1D = M1B = r1 + d In vierhoek AEDB geldt nu α + α + β + β = 360 ⇒ α + β = 180º dus twee hoeken tegenover elkaar zijn 180º. Dan is AEBD een koordenvierhoek. |
||||
| b. | Door
de gelijkbenige driehoeken M2CB en M2DA te
bekijken kun je op precies dezelfde manier als in opgave 15 bewijzen dat
ADCB ook een koordenvierhoek is. De cirkel door AEDB is de omgeschreven cirkel van driehoek ADB De cirkel door ADCB is ook de omgeschreven cirkel van driehoek ADB. Kortom; alle vijf de punten liggen op deze omgeschreven cirkel. |
||||
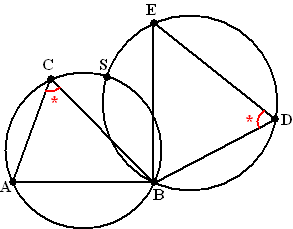
| 15. | ∠ASB
= ∠ACB (beiden de omtrekshoek van boog
AB) dus ∠ASB = * BSED is een koordenvierhoek, ∠ASB + ∠BSE
= * + 180º - * = 180º
|
|
|||
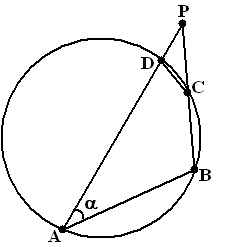
| 16. | a. | ∠BCD
= 180 -
α (want ABCD is een
koordenvierhoek. Dus is ∠DCP = α Maar ∠CPD = α want driehoek ABP is gelijkbenig met tophoek B. Als ∠DCP = ∠CPD is driehoek CDP óók gelijkbenig met tophoek D. Dus DP en DC zijn even lang. |
|
||
| b. | Driehoek
CDP is gelijkbenig met basishoeken DCP = CPD =
α
(zie antwoord 16) Dus ∠PDC = 180 - 2α (hoekensom driehoek) Dus ∠ADC = 2α (samen een gestrekte hoek) ∠ACD = 90º (want AD is een middellijn) dus ∠DAC = 90º - 2α (hoekensom driehoek DAC) ∠CAB = ∠DAB - ∠DAC = α - (90 - 2α) = α - 90 ∠ABD = 90º (want AD is een middellijn) Dan is ∠BSA = 180º - ∠SAB - 90º = 180 - 3α + 90 - 90 = 180 - 3α Dan is ∠ASD = 3α (samen 180º) |
|
|||
| 17. | a. | hoek BAL = hoek
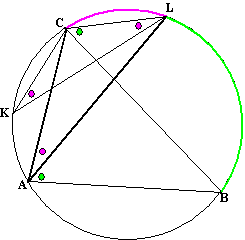
BCL (beiden omtrekshoek van BL) hoek LAC = hoek CKL (beiden omtrekshoek van CL) hoek CKL = hoek CLK (gelijkbenige driehoek CKL) dus BAC = BAL + LAC = BCL + CKL = BCL + CLK = QCL + CLK |
|
||
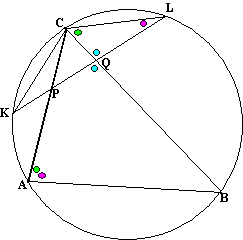
| b. | hoek PQB = hoek
CQL (overstaande hoeken) Uit de vorige vraag bleek dat BAC = QCL + QLC Maar QCL + QLC + CQL = 180º (hoekensom driehoek) De drie verschillende kleurtjes hiernaast zijn dus samen 180º Dus is ook BAC + PQB = 180º Dus is APQB een koordenvierhoek
|
|
|||
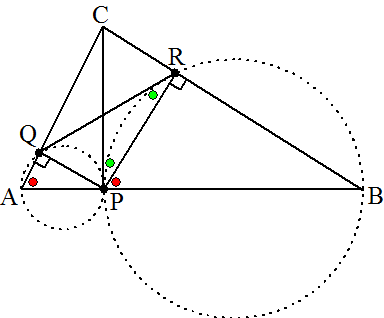
| 18. | ∠AQP
en ∠PRB zijn 90º (Thales) Dus is QPRC een rechthoek De groene hoeken zijn gelijk (rechthoek) De rode hoeken zijn gelijk (F-hoeken) Een rode en een groene zijn samen 90º (rechte hoek bij P) ∠BAQ + ∠QRB = 180º (rood + groen + 90) Overstaande hoeken 180º betekent dat AQRB een koordenvierhoek is. |
 |
|||
| 19. |
|
||||
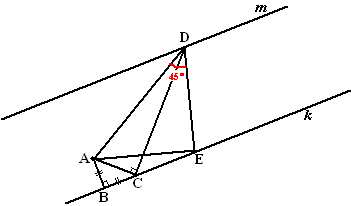
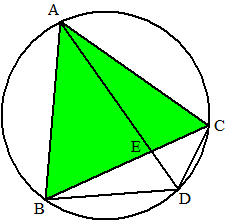
| a. | AB =
BC dus ABC is gelijkbenig ∠CBA = 90º dus ÐBCA = 45º ∠ACE = 135º want de hoeken bij C zijn samen 180º ∠ACE + ∠ADE = 135º + 45º = 180º dus is de vierhoek een koordenvierhoek. |
||||
| b. | Omdat
ACED een koordenvierhoek is liggen de punten A, C, D en E op een cirkel. ∠AED = ∠ACD = 90º (omtrekshoek van AD) ∠DAE = 45º (in driehoek AED zijn de hoeken samen 180º) Driehoek ADE heeft twee gelijke hoeken (van 45º) dus is de driehoek gelijkbenig. Bovendien heeft de driehoek een rechte hoek (∠AED) Dus is het een geo-driehoek. |
||||
| 20. | Stel dat twee van die cirkels
elkaar in S snijden. Dan is hoek ASC = 120º want omdat ASCD een koordenvierhoek is moet die hoek samen met de hoek bij D 180º zijn Om dezelfde reden is ∠ASB = 120º Maar dan is ook ∠CSB 120º (samen 360º) Dus is CSBF ook een koordenvierhoek Dus ligt S ook op de omgeschreven cirkel van de andere driehoek. |
|
|||
| 21. |
|
||||
| a. | ∠APB = 90º (Thales),
Dus ∠BAP + ∠ABP
= 90º (hoekensom driehoek ∠ABP'= 90º (raaklijn aan cirkel), Dus ∠BAP + ∠AP'B = 90º (hoekensom driehoek) ∠BAP is zowel met ∠ABP als met ∠AP'B samen 90º dus zijn die twee hoeken aan elkaar gelijk. |
||||
| b. | Het is voldoende om aan te tonen dat twee
hoeken van vierhoek PQQ'P' die tegenover elkaar liggen samen 180º zijn,
want dan is de vierhoek een koordenvierhoek dus liggen de punten op één
cirkel. We gaan aantonen dat ∠PQQ' + ∠AP'B = 180º ∠ABP = ∠AQP (constante hoek) ∠ABP = ∠AP'B (vraagstuk a) Dus is ∠AQP = ∠AP'B Maar ∠AQP + ∠PQQ' = 180º (gestrekte hoek) dus zijn ook ∠AP'B + ∠PQQ' samen 180º. q.e.d. |
||||
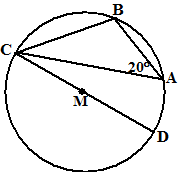
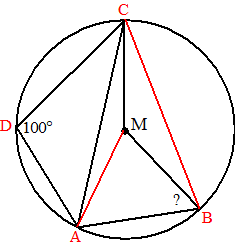
| 22. | Omdat CD een middellijn is, is
∠CAD = 90º (Thales) Dus is ∠BAD = 90 + 20 = 110º Omdat CDAB een koordenvierhoek is, is ∠BAD + ∠BCD = 180º Dus is ∠BCD = 70º |
|
|||
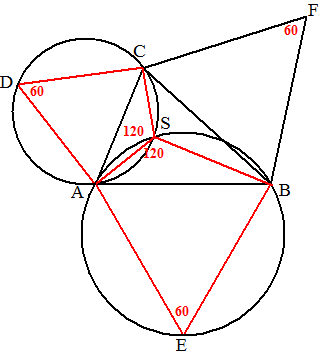
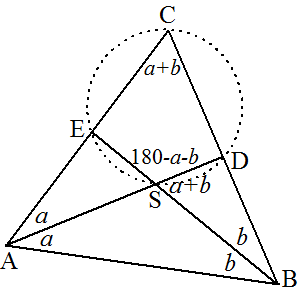
| 23. | Noem de hoeken even a en
b ∠BSD = a + b (buitenhoek driehoek ASB) ∠DSE = 180 - a - b (gestrekte hoek BSE) ∠C = a + b (koordenvierhoek ESDC) hele driehoek: 3a + 3b = 180º Dan is ∠C = a + b = 60º |
|
|||
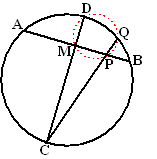
| 24. | APQB is een
koordenvierhoek dus ∠PAB + ∠PQB = 180º Maar ∠PQB + ∠PQM is ook 180º (gestrekt) Dus ∠PQM = ∠PAB (rood) ∠PQM = ∠QPM (gelijkbenige driehoek) (rood) Dus ∠QPM = ∠PAB Dan is AB // PQ (F-hoeken) Dan is ∠PBA = ∠BPQ (Z-hoeken) (blauw) maar ∠PBA is de omtrekshoek van koorde PA en ∠BPQ is de omtrekshoek van koorde BQ De koorden BQ en PA hebben dezelfde omtrekshoek dus zijn gelijk. |
|
|||
| 25. |
∠PQR = ∠PSR
(beiden de omtrekshoek van koorde PR) ∠PQR = ∠BAQ (Z-hoeken) Dus is ∠BAQ = ∠PSR ......(1) ∠BSR = 180º - ∠PSR (gestrekte hoek) ∠BSR + ∠PSR = 180º Maar vanwege (1) is dan ook ∠BSR + ∠BAQ = 180º Dus is de vierhoek een koordenvierhoek. |
|
|||
| 26. | ∠ABD =
oo (gelijkbenige driehoek) ∠ACD = ooo (buitenhoek ABC) ∠AED = 180 - ooo (koordenvierhoek) hoekensom ADE: ∠D = 180 - o - (180 - ooo) = oo |
|
|||
| 27. | a. |
∠BAC = ∠BDC
(beiden omtrekshoek van BC) ∠BCA = ∠BDA (beiden omtrekshoek van BA) Dus ∠BCA = ∠BAC Dus driehoek ABC is gelijkbenig met top B (gelijke basishoeken) Dus is BA = BC. |
|
||
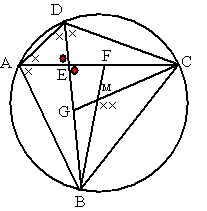
| b. | de vier hoeken met een kruisje zijn allemaal
gelijk (zie vraag a) ∠BMC is het dubbele daarvan (middelpuntshoek van BC is dubbel zo groot als omtrekshoek van BC) ∠GMF is dus ook gelijk aan twee kruisjes (overstaande hoeken) De rode hoek is samen met twee kruisjes gelijk aan 180º (in driehoek AED). De rode hoek daartegenover dus ook (overstaande hoeken) Dus ∠GEF (rood) + ∠GMF (twee kruisjes) = 180º Dan is EGMF een koordenvierhoek. |
|
|||
| 28. | a. |
|
|||
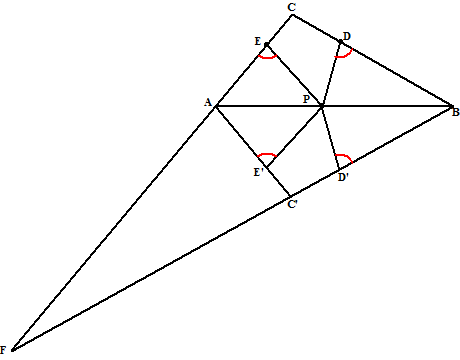
| Vanwege het spiegelen is
∠PDB = ∠PD'B Maar omdat de rode hoeken gelijk zijn is dan ook ∠PD'B = ∠PEA PDÇ is samen met PD'B 180º dus ook samen met PEA Als ∠PDC + ∠PEA = 180º dan is FD'PE een koordenvierhoek |
|||||
| b. | Construeer een cirkel door de
drie bekende punten F, D', E (middelloodlijnen van FE en FD' met
elkaar snijden voor het middelpunt) Die cirkel snijdt AB in P. |
||||
| 29. |
|
||||
| ∠ACS
= ∠NMS ∠MBN = ∠MAN = 90º (raaklijnen aan een cirkel) Dus is MN middellijn van een cirkel door A en B (Thales) Dus is MBNA een koordenvierhoek ∠AMN = ∠ABN (omtrekshoeken van AN) Op dezelfde manier is BSAC ook een koordenvierhoek (hoeken B en A 90º) ∠ABN = ∠ACS (omtrekshoeken van AS) Dus is ∠AMN = ∠ACS (beiden gelijk aan ∠ABN) |
|||||
| 30. | a. |
∠CMB = 2 ∠CAB
(middelpuntshoek en omtrekshoek van koorde CB) .....(1) ∠CBM = ∠BCM (gelijkbenige driehoek, want MC en BM zijn beiden de straal van de cirkel) Som van de hoeken in driehoek CMB geeft ∠CMB + 2 ∠CBM = 180º ∠CBM = 1/2(180 - ∠CMB) met (1) geeft dat: ∠CBM = 1/2(180 - 2∠CAB) ∠CBM = 90 - ∠CAB |
|
||
| b. |
∠CQP = 90 + ∠CBM
(buitenhoek van driehoek BQN met het resultaat van vraag 12: ∠CQP = 90 + (90 - ∠CAB) ∠CQP + ∠CAB = 180 Dus is CAPQ een koordenvierhoek. |
|
|||
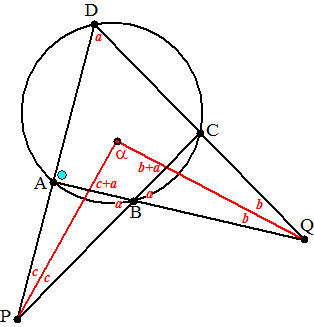
| 31. | Stel de hoek bij D gelijk aan
a Dan is ∠ABC = 180 - a (koordenvierhoek), dus de andere hoeken bij B zijn ook gelijk aan a (gestrekte hoek: zie tekening) Noem de hoeken bij P en Q c en b Daaruit volgende hoeken c + a en b + a in de figuur hiernaast (buitenhoeken) De vierhoek met a erin heeft dan som van de hoeken a + (c + a) + (b + a) + (180 - a) = 360º dus a = 180º - (a + b + c) .....(1) Maar de blauwe hoek is gelijk aan a + 2c (buitenhoek) hoekensom driehoek AQD: 2b + a + (a + 2c) = 180º dus a + b + c = 90º Dan geeft (1) dat α = 180º - 90º = 90º |
|
|||
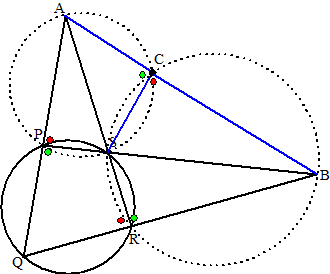
| 32. | Noem ∠QRS
= a Dan is ∠QPS 180 - a (koordenvierhoek QRSP) Dan is ∠APS = a (gestrekte hoek) Dan is ∠ACS = 180 - a (koordenvierhoek ACSP Verder is ∠BRS = 180 - a (gestrekte hoek) Dan is ∠SCB = a (koordenvierhoek RSCB) De hoeken bij C zijn samen 180º dus C ligt op AB. |
|
|||
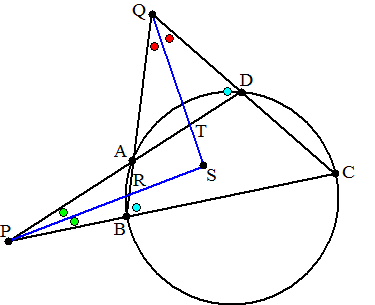
| 33. | Zie de figuur hiernaast. Noem de aangegeven hoeken R (rood) B (blauw) en G (groen) ∠PDC = 180º - B (gestrekte hoek) Dus ∠ABC = B (koordenvierhoek) Dus ∠PBA = 180º - B ∠PAQ = RRB (buitenhoek driehoek QAD) Dus ÐPAB = 180º - RRB (gestrekte hoek) Hoekensom driehoek PAB: GG + 180º - RRB + 180º - B = 180º Daaruit volgt R + B - G = 90º .....(1) ∠PTQ = R + B (buitenhoek driehoek QTD) dus ∠PTS = 180º - R - B (gestrekte hoek) Hoekensom PST: G + S + 180º - R - B = 180º Daaruit volgt S = R + B - G Met (1) geeft dat S = 90º |
|
|||
| 34. | ∠ABD = ∠ACD (omtrekshoek AD) ∠BAC = ∠BDC (omtrekshoek BC) groen plus rood zijn samen 90º (bijv. hoekensom BSA) Dat geeft de hoeken DSP en CSP Dat geeft de hoeken ASQ en BSQ (overstaande hoeken) De driehoeken ASQ en BSQ zijn gelijkbenig Dus AQ = SQ = QB Dus Q is het midden van AB |
|
|||
| 35. | ∠QAB + ∠BPQ = 180º (koordenvierhoek) ∠BPQ + ∠QPD = 180º (gestrekte hoek) dus ∠QPD = ∠QAB ∠QDP + ∠QCD = 180º (koordenvierhoek) ∠QCD + ∠DCP = 180º (gestrekte hoek) Dus ∠DCP = ∠QPD = ∠QAB Dan is AB // CD (F-hoeken) |
|
|||
| 36. |
|
||||
| ∠BDE = ∠BFD (hoek tussen koorde DE en
raaklijn) ∠BDE = ∠BAC (F-hoeken) dus ∠BFD = ∠BAC omdat ∠BFD + ∠DFC = 180º (gestrekte hoek) is ook ∠BAC + ∠CFD = 180º Dus is ADFC een koordenvierhoek (overstaande hoeken samen 180º) |
|||||
| 37 | MR is
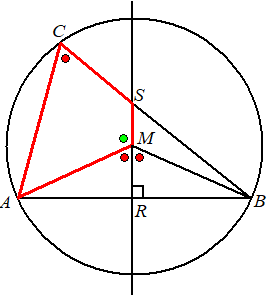
middelloodlijn van AB dus AR = RB MR = MR Dus driehoek AMB is gelijkbenig met gelijke basishoeken Dus AMR en BMR zijn gelijkvormig (ZZR) Dus is ∠AMR = ∠BMR Maar ∠ACB = 1/2 ∠AMB (koorde AB) Dus ∠ACB = ∠AMR Rood plus groen hiernaast is 180º (gestrekte hoek bij M Dus ∠ACS + ∠AMS = 180º Dan is AMSC een koordenvierhoek. |
|
|||
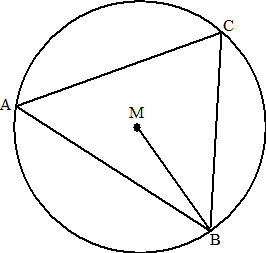
| 38. | ∠ABC = 80
(koordenvierhoek) ∠AMC = 160 (middelpuntshoek) ∠MAC = 10 (gelijkbenig) ∠MAB = 61 = MBA (gelijkbenig) |
|
|||
| 39. |
|
||||
| Verleng DC en AB tot
ze elkaar snijden in H. ∠DCB = 180 - α (koordenvierhoek) dus ∠HCB = α De driehoeken HCB en FAE en HAD en HFG zijn gelijkvormig. tanα = 2 dus DH = 2 AD = 2√450 AEF is gelijkvormig met FGH dus AE/FG = EF/GH Noem de zijden van het vierkant x, dan geldt: (√450 - x)/(x) = (x)/(2√450 - x) x2 = (√450 - x)(2√450 - x) = 900 - 3x√450 + x2 3x√450 = 900 x = 300/√450 = 300/450 √450 = 10√2 De diameter van de cirkel is dan 20, dus de oppervlakte is 100ππ |
|||||
| 40. | ABDC is een
koordenvierhoek, dus hoek D is 120° oppBCD = oppBDE + oppCDE BD CD sin120 = BD DE sin60 + CD DE sin60 maar sin60 = sin120, dus: BD CD = BD DE + CD DE BD CD = DE (BD + CD) DE = BD CD/(BD + CD) |
|
|||
|
© h.hofstede (h.hofstede@hogeland.nl) |
|||||