Nieuwe pagina 1

© h.hofstede (h.hofstede@hogeland.nl)

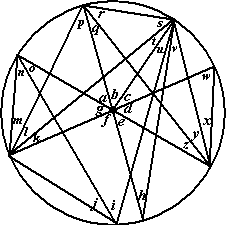
a - m, z
b - y
c - x , k
d - geen
e - v, q
f - geen
g - j

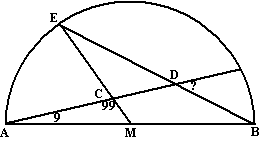
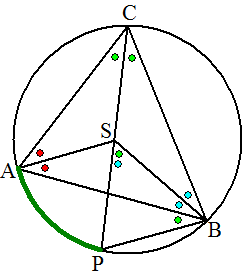
∠AME = 180 - 9 - 99 = 72º

Dan is ∠ABE de helft daarvan (omtrekshoek van koorde AE): 36º

∠BME = 108º (samen een rechte lijn met ∠AME)
∠MCD = 81º (samen een rechte lijn met ∠ACM)

Dan is ∠BDA = 360 - 108 - 81 - 36 = 135º
Dan is de vraagteken hoek 180 - 135 = 45º

De middelpuntshoek is ¹/₅ • 360 = 72º
Dan is de omtrekshoek 36º

De middelpuntshoek is dan ³⁶⁰/_n
De omtrekshoek is dan ¹⁸⁰/_n

De omtrekshoek van koorde AC is hoek B van de driehoek
De omtrekshoek van koorde BA is hoek C van de driehoek.

Samen zijn die de omtrekshoek van koorde BC
De middelpuntshoek daarvan is ∠BMC
Die is dus dubbel zo groot als de hoeken B en C van de driehoek

∠CDB is constant want is gelijk aan ∠ADB en dat is de omtrekshoek van koorde AB

∠ACB is constant want is de omtrekshoek van koorde AB.
Dus is ∠BCD ook constant (180º - ∠ACB)

Van driehoek BCD liggen twee hoeken vast, dus de derde ook, dus is ∠CBD constant.

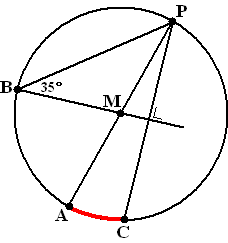
trek lijn BM door totdat hij de cirkel snijdt in Q.

De omtrekshoek van PQ is dan 35º
De middelpuntshoek van PQ is dan 70º
Dat is hoek PMQ dus die is 70º

Dan is hoek APC 20º (vanwege de rechte hoek tussen PC en BQ)
Dan is hoek AMC 40º (het is de middelpuntshoek van AC)

AC is dus ¹/₉ deel van de cirkel.
De hele omtrek is 2 • π • 8, dus AC heeft lengte ¹⁶/₉π

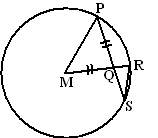
∠QMP = ∠QPM (basishoeken gelijkbenige driehoek)

∠QMP is ook de middelpuntshoek van PR.
∠QSR is de omtrekshoek van PR, dus 2 • ∠QSR = ∠QMP

∠MQP = 180º - 2 • ∠QMP
∠MQP = ∠SQR (overstaande hoeken)
Dus ∠SQR = 180 - 2 • ∠QMP
Met het rode resultaat hierboven geeft dat
∠SQR = 180 - 4 • ∠QSR

∠QRS = 180 - ∠SQR - ∠QSR (driehoek QRS)
= 180 - (180 - 4 • ∠QSR) - ∠QSR
= 3 • ∠QSR

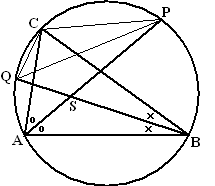
∠CPQ = ∠CBQ (constante hoek) dus ∠CPQ is ook een "kruisje"
∠QPS = ∠QBA (constante hoek) dus ∠QPS is ook een "kruisje"

∠CQP = ∠CAP (constante hoek) dus ∠CQP is ook een "rondje"
∠PQB = ∠PAB (constante hoek) dus ∠PQB is ook een "rondje"

De driehoeken CQP en SQP hebben beiden een hoek met een "kruisje" en eentje met een "rondje"
Verder hebben ze zijde QP gemeenschappelijk
Dus zijn de driehoeken congruent (HZH)

∠APC is constant (omtrekshoek van AC)
Dus is ∠QRP constant (hoekensom driehoek QRP)
Dus is ∠CRB constant (overstaande hoeken)

Omdat ∠BRC constant is liggen B, C en alle punten R op één cirkel.
Teken de middelloodlijn van RC en die van BR. Waar deze twee middelloodlijnen elkaar snijden ligt het middelpunt van de gezochte cirkel.

Die cirkel kun je dan tekenen (rode cirkel hiernaast)

ABP mag geen stompe hoek hebben.
Teken de grensgevallen AP en BP waarbij de driehoek ABP rechthoekig is (blauw hiernaast).

Verbind C met beide punten P, en je snijdt een stuk van de rode cirkel af waar R op moet liggen.
(het groene deel hiernaast)

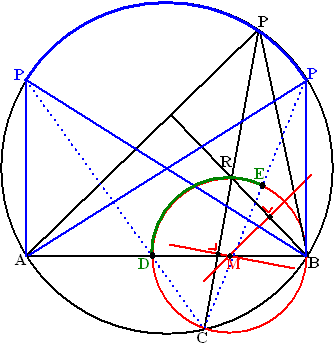10.

∠ADB is de omtrekshoek van boog AB

∠DAC is de omtrekshoek van boog CD

∠ADB + ∠DAC zijn dan samen 90º want als AB en CD samen de helft van de cirkel zijn, zijn hun middelpuntshoeken samen 180º , dus hun omtrekshoeken samen 90º

Als S het snijpunt van de diagonalen is, is dan ∠ASD ook 90º (hoekensom driehoek ADS)

Dus staan de diagonalen loodrecht op elkaar.

11.

∠PSB is groen plus blauw (buitenhoek driehoek CSB)
∠PBA = ∠ACP (omtrekshoek AP)
Dus ∠PBS = groen plus blauw

∠PBS = ∠BSP dus driehoek BSP is gelijkbenig.

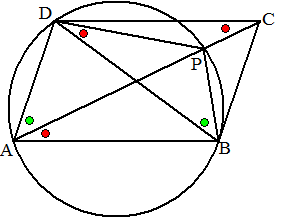
12.

∠PDB = ∠PAB (omtrekshoek PB)
∠PAB = ∠ACD (Z-hoeken)
∠DAC = ∠DBP (omtrekshoek DP)

Dus de driehoeken ACD en BDP zijn gelijkvormig (HH)
Dan is ^AD/_AC = ^BP/_BD
Daaruit volgt AD • BD = AC • BP