|
|||||
| 1. | Propositie 7 zegt: Twee punten C en D liggen aan dezelfde kant naast lijnstuk AB. Als AC = AD en BC = BD dan zijn C en D hetzelfde punt. Dat betekent in dit geval dat F en C' wel hetzelfde punt moeten zijn. Dus vallen de driehoeken volledig samen, en dus zijn ze congruent. (A4) |
||||
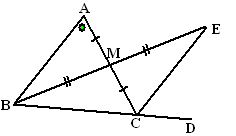
| 2. | a. | ∠AMB = ∠CME (overstaande hoeken) AM = CM BM = EM Dus zijn de driehoeken AMB en CME congruent (ZHZ) |
|
||
| b. | Vanwege de congruentie van vraag
a) is ∠BAC = ∠ACE Maar ∠ACD = ∠ACE + ∠ECD Dus ∠ACD > ∠ACE = ∠BAC. |
||||
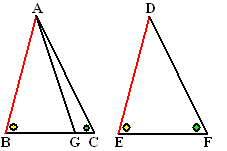
| 3. | a. | ∠GBA = ∠FED AB = DE BG = EF Dus zijn de driehoeken BGA en EFD congruent (ZHZ) |
|
||
| b. | Vanwege deze congruentie is
∠BGA = ∠EFD Maar ook geldt ∠BCA = ∠EFD Dus is ∠BGA = ∠BCA (A1) Maar als je driehoek AGC bekijkt, dan is ∠BGA een buitenhoek en ∠BCA een gewone hoek. Volgens de vorige opgave moet ∠BGA altijd groter zijn dan ∠BCA. Dat klopt dus niet. |
||||
| c. | Dat heet een "bewijs
uit het ongerijmde" We begonnen met aan te nemen dat er een punt G bestaat (dus een tweede driehoek die óók congruent met de eerste is). Maar daardoor kwamen we uit op iets onmogelijks (vraag b)). Dus klopt die aanname niet: er bestaat niet zo'n punt G. Dus er is maar één manier voor de driehoeken met twee gelijke hoeken en een gelijke zijde te tekenen. Dus zijn die driehoeken congruent. |
||||
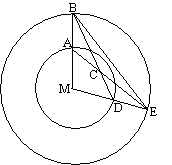
| 4. | a. | BA = DE (beiden zijn de
grote straal min de kleine) BE = BE ∠ABE = ∠DEB (want driehoek MBE is gelijkbenig, omdat NB en ME allebei de straal van de cirkel zijn)) Dus zijn de driehoeken ABE en DEB congruent (ZHZ) |
|
||
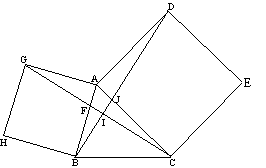
| b. | BA = GA (vierkant) AD = AC (vierkant) ∠GAC = ∠BAD (beiden zijn ∠BAC plus een rechte hoek) Dus zijn de driehoeken GAC en BAD congruent (ZHZ) |
 |
|||
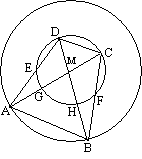
| c. | AM = MB (straal van de
grote cirkel) MD = MC (straal van de kleine cirkel) ∠AMD = ∠BMC (overstaande hoeken) Dus zijn de driehoeken AMD en BMC congruent (ZHZ) |
|
|||
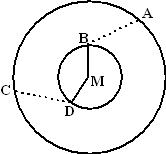
| 5. | MB = MD (straal
kleine cirkel) MA = MC (straal grote cirkel) BA = DC (gegeven) Dus zijn de driehoeken MBA en MDC congruent (ZZZ) |
|
|||
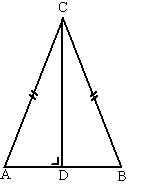
| 6. | AC = BC
(gelijkbenige driehoek) DC = DC ∠ADC = ∠BDC = 90º (hoogtelijn) dus zijn de driehoeken ADC en BDC congruent (ZZR) Dus is AD = BD Dus is D het midden van AB. |
|
|||
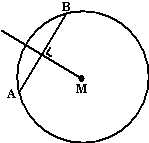
| 7. | Omdat MB = MA
(straal van de cirkel) is MBA een gelijkbenige driehoek. In de vorige opgave is bewezen dat dan geldt dat de basis AB in twee gelijke delen wordt verdeeld door de hoogtelijn vanuit de top. Dat hoeven we dus nu niet wéér te doen!! |
|
|||
| 8. | a. |
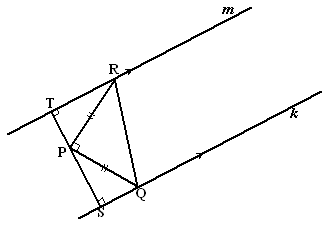
∠SPQ + ∠SQP = 90º
(samen met de rechte hoek QPR zijn het de hoeken van een driehoek) ∠SPQ + ∠TPR = 90º (samen met de rechte hoek QPR vormen ze een gestrekte hoek) Dus ∠SQP = ∠TPR ∠PSQ = ∠PTR (= 90º) PR = PQ Dus zijn de driehoekencongruent (ZHH) |
 |
||
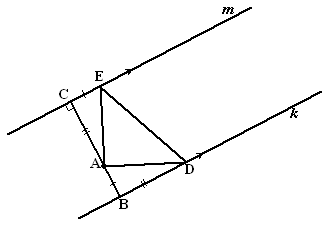
| b. | Teken een lijn
door punt A loodrecht op k en m. Noem de snijpunten met
k en m respectievelijk B en C Teken nu E en D zó dat CE = AB en BD = AC (zie de figuur hiernaast) Dan zijn de driehoeken ACE en ABD congruent en is de driehoek een geodriehoek. |
 |
|||
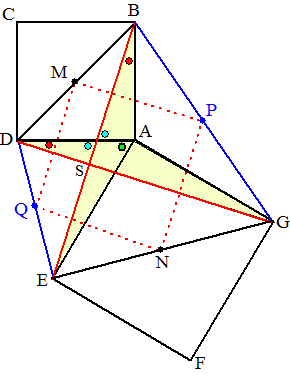
| 9. | a. | AB = AD AE = AG ∠DAG = ∠BAE (beiden een rechte hoek plus de groene hoek) Dus de driehoeken zijn congruent (ZHZ) |
|
||
| b. | MP // DG (middenparallel
driehoek BDG) QN // DG (middenparallel driehoek EDG) Dus MP en QN zijn evenwijdig, en ook even lang omdat beiden de helft van DG zijn MQ // EB (middenparallel driehoek DEB) PN // EB (middenparallel driehoek GEB) Dus MQ en PN zijn evenwijdig en ook even lang omdat beiden de helft van EB zijn Nu nog bewijzen dat DG en EB loodrecht op elkaar staan: De rode hoeken zijn gelijk (vraag a) De blauwe hoeken zijn gelijk (overstaand) Dus is ∠DSB = ∠DAB = 90º MQNP heeft allemaal even lange zijden en allemaal rechte hoeken. Dus het is een vierkant. |
||||
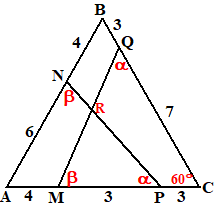
| 10. | Zie de afmetingen
hiernaast. De driehoeken PAN en QCM zijn congruent (ZHZ) Dus de hoeken α en β hiernaast zijn gelijk. In driehoek QMC kun je zien dat α + β = 120º Dus in driehoek MPR ook. Dus is de gezochte hoek 60º |
|
|||
|
© h.hofstede (h.hofstede@hogeland.nl) |
|||||