© h.hofstede (h.hofstede@hogeland.nl)

       
1. a. x' = sin(2t)    
y' = 2sin2tcost
v = √(sin2(2t) + 4sin4tcos2t)
de kromme wordt één keer doorlopen voor  -1/2π < t < 1/2π

Y1 = √( (sin(2X))^2+4(sin(X))^4*(cos(X))^2)
calc - ∫f(x)dx  voor  X = -1/2π  tot X = 1/2π  geeft lengte L = 2,438
       
  b. y = 2/3x√x
y = 2/3x1,5
2/3sin3t    ?=?   2/3 • (1/2-1/2cos(2t))1,5 
sin3t   ?=?  (1/2-1/2(1 - 2sin2t))1,5
sin3t   ?=?  (1/2-1/2 + sin2t)1,5
sin3t   ?=?  (sin2t)1,5
sin3t   ?=?  sin3t
q.e.d.
       
  c.
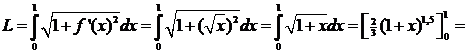    = 2/3 • 2√2 - 2/3 • 1
= 4/3√2 - 2/3
De lengte van de kromme is dan het dubbele daarvan (boventak plus ondertak):  8/3√2 - 4/3 ≈  2,438
       
2. a. x(t) = t3 - at = 0
t(t2 - a) = 0
t = 0   ∨   t = √a  ∨  t = -√a

t = 0 geeft y = 0
t = ±√a geeft  y = a en dat is inderdaad het punt  (0, a)
       
  b. x ' = 3t2 - a
y ' = 2t
v = √((3t2 - a)2 + 4t2)
Dat is minimaal als dat deel onder de wortel minimaal is, en dat is zo als de afgeleide ervan nul is.
(3t2 - a)2 + 4t2 = 9t4 - 6at2 + a2 + 4t2
afgeleide:  36t3 - 12at + 8t = 0
t(36t2 - 12a + 6) = 0
t = 0 ∨  36t2 = 12a - 6
t = 0  ∨  t = ±√(1/3a - 1/6)

raaklijn evenwijdig aan de y-as:  x ' = 0
3t2 - a = 0
t2 = 1/3a
t = ±√(1/3a)

Dat is niet hetzelfde....
       
  c. Het lusje bevindt zich tussen t = -√2 en t = √2  (zie vraag a)
v = √((3t2 - 2)2 + 4t2)  (zie vraag b)

Y1 = √((3X^2 - 2)^2 + 4X^2)
calc - ∫f(x)dx -  tussen X = √2 en X = -√2 geeft lengte  L = 6,37
       
3. a. x  = 0
2cost + cos(2t) = 0
2cost +  (2cos2t - 1) = 0
2cos2t + 2cost - 1 = 0
cost =  (-2 ±√(4 + 8))/4 = -1/2 ± 1/2√3

alleen de oplossing  cost = -1/2 + 1/2√3 is mogelijk, en geeft 
t = 1,196 ∨  t = 4,338
dan is  y = 2sint - sin(2t) = 1,18  ∨  -1,18

y = 0
2sint - sin(2t) = 0
2sint - 2sintcost = 0
2sint(1 - cost) = 0
sint = 0  ∨  cost = 1
t =  0  ∨   t = π
dan is x =  2cost + cos(2t) = 3  of  -1  

       
  b. x'  = -2sint - 2sin(2t)  dus  x'(1/4p) = -√2 - 2
y ' =  2cost - 2cos(2t)   dus  y '(1/4p) = √2
   
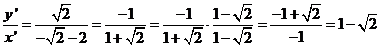    Het raakpunt is het punt (√2, √2 - 1)  
    √2 - 1 = (1 - √2) · √2 + b
√2 - 1 = √2 - 2 + b
b = 1
De raaklijn is de lijn  y = (1 - √2)x + 1
       
  c. v2  =  x ' 2 + y ' 2  = (-2sint - 2sin(2t))2 + (2cost - 2cos(2t))2 
v2 = 4sin2t + 8sintsin2t  + 4sin2(2t) + 4cos2t - 8costcos(2t) + 4cos2(2t)
v2 = 4 + 4 + 8(sintsin2t  - costcos2t)
v2 = 8 + 8sin(-t)       want  sinacosb - cosasinb = sin(a - b)
v2 = 8 - 8sint
v = √(8 - 8sint)
       
  d. Y1 = √(8 - 8sin(X))
calc - ∫f(x)dx  van  X = 0 tot X = 2π  geeft  L = 16
       
4. a. een beetje proberen geeft als gauw  a = 1/2π denk ik...
       
  b. cost + cos(3t)  ?=?   2(sint - 1/2π) + 4sin3(t - 1/2π)
cost + cos(3t)  ?=?  -2cost - 4cos3t     want  sin(t - 1/2π) = -cost
cost + cos(2t + t)  ?=?  -2cost - 4cos3t   
cost + cos2tcost - sin2tsint   ?=?  -2cost - 4cos3t   
cost + (2cos2t - 1)cost - 2sintcostsint  ?=?  -2cost - 4cos3t   
cost + 2cos3t  - cost  -  2(1 - cos2t)cost   ?=?  -2cost - 4cos3t   
2cos3t - 2cost + 2cos3t   ?=?   -2cost - 4cos3t   
-2cost + 4cos3t   ?=?  -2cost - 4cos3t   
q.e.d.
       
  c. sin(t + 1/3π) = 0
t + 1/3π = 0  ∨  t + 1/3π = π
t = -1/3π ∨  t = 2/3π

t = -1/3π   geeft  y = cos(-1/3π) + cos(-π) = 1/2 - 1 = -1/2
t = 2/3π   geeft  y = cos(2/3π) + cos(2π) = -1/2 + 1 = 1/2
De afstand daartussen is 1.
       
  d. x ' =  cos(t + 1/6π)  dus  x'(1/3π) = cos(1/3π + 1/6π) = cos(1/2π) = 0

y ' =  -sint - 3sin3t  dus  y '(1/3p) = -sin(1/3π) - 3sinπ =  -1/2√3

Dat is dus geen keerpunt, want  y' is niet gelijk aan 0.
       
5. a. x ' = cost
y ' = 2cos(t - 1/2π) = 2sint
v = √(cos2t + 4sin2t) = √(1 - sin2t + 4sin2t) = √(1 + 3sin2t)
       
  b. Y1 = √(1 + 3(sin(X))^2)
calc - ∫f(x)dx  van  X = 0 tot X = 2π geeft L = 9,69		  
       
  c. de punten met verticale raaklijn zijn de punten waar x ' = 0 dus waar cost = 0
dat zijn dus de punten waarbij  t = 1/2π  en  t = 3/2π horen
bij deze ellips zijn dat de punten  (-1, 1)  en  (1, -1)   (bedenk dat y van -2 tot 2 loopt)
bij t = 1/2π  heeft x een maximum, dus dat is het rechterpunt, dus dan is y = -1

2sin(1/2π - aπ) = -1
sin(1/2π - aπ) = -1/2
1/2π - aπ = 7/6π  ∨  1/2π - aπ = 11/6π
a = -2/3   ∨   a = -4/3
Tussen 0 en 2π geeft dat  a = 2/3 ∨  a = 4/3
       
6. a. K snijdt zichzelf in de oorsprong.

x = 0
cos2t = 0
2t = 1/2π + k2π  ∨  2t = 3/2π + k2π
t = 1/4π + kπ  ∨  t = 3/4π + kπ
dat geeft  t = 1/4π,  3/4π,  5/4π,  7/4π

y = cost + sint = 0
y(1/4π) = y(5/4π) = √2
y(3/4π) = y(7/4π) = 0  dus de gezochte t-waarden zijn  3/4π en 7/4π

x ' = -2sin(2t)  dus  x' (3/4π) = 2  en  x '(7/4π) = 2
y ' = -sint + cost  dus   y' (3/4π) = -√2   en  y '(7/4π) = √2

de helling in t =  3/4π  is -1/2√2 en dat maakt een hoek van  tan-1(-1/2√2) = -35,26º met de horizontaal
de helling in t =  7/4π  is 1/2√2 en dat maakt een hoek van  tan-1(1/2√2) = 35,26º met de horizontaal

de kromme snijdt zichzelf dan onder een hoek van  2 • 35,26 ≈ 70º
       
  b. cos22t + ((cost + sint)2 - 1)2   ?=?   1
cos22t + (cos2t + 2costsint + sin2t - 1)2  ?=?  1
cos22t + (1 + 2costsint - 1)2  ?=?  1
cos22t + (sin2t)2  ?=?  1
1  ?=?  1

q.e.d.
       
  c. P = (cos2t,  cost + sint)
OP met Pythahoras:

OP2 = (cos22t) + (cost + sint)2
OP2 = cos22t + cos2t + 2costsint + sin2t
OP2 = cos22t + sin2t + 1

OP is maximaal als OP2 maximaal is.
de afgeleide van OP2 moet dus nul zijn:
-2cos(2t)•sin(2t) • 2 + 2cos(2t) = 0
2cos(2t) • (-2sin(2t) + 1) = 0
cos2t = 0 ∨  sin2t = 1/2
2t = 1/2π  ∨ 2t = 3/2π  ∨  2t = 1/6π  ∨ 2t = 5/6π   (alles + k2π)
dat geeft  t =  1/4π,  3/4π, 5/4π,  7/4π,  1/12π,  13/12π, 5/12π, 17/12π 
De maxima vind je bij  t =  1/12π,  13/12π, 5/12π, 17/12π   en die zijn allemaal gelijk aan 21/4.

Als OP2 = 21/4, dan is OP = 11/2
       
7. a. sos-cas-toa in driehoek MPV: (MV = 1)
cost = MP/MV = MP/1 =  MP
sint  = VP/MV = VP/1 = VP

xV = (horizontale plaats van M) - (VP) = t - sint
yV = (verticale plaats van M) - (MP) = 1 - cost

Dat geeft de volgende plot:
   
       
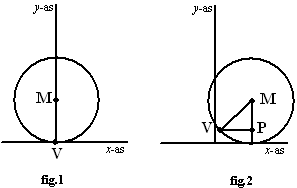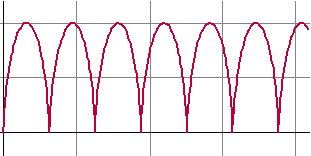  b. 1 - cos t = 0,5
cost  = 1/2
t = 1/3π Ú  t = 12/3π
t = 1/3π  geeft  x = 1/3π - 1/2√3
t = 12/3π geeft  x = 12/3π - - 1/2√3

Het verschil daartussen is 11/3π + √3
       
  c. x ' = 1 - cost
y ' = sint

v = √((1 - cost)2 + sin2t)  = 1
√(1 - 2cost + cos2t + sin2t) = 1
1 - 2cost + 1 = 1
2cost = 1
cost = 1/2
t = 1/3π  ∨  t =  12/3π    (+ k2π)
       
  d. Een punt van V is  P = ( t - sint , 1 - cost )
De lijn naar de oorsprong heeft dan helling:   Δy/Δx =  (1 - cost)/(t - sint)  en dat is het gezochte functievoorschrift
       
8. a. x = 0  
   
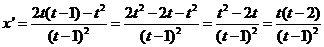    Dat is nul voor t = 0  en t = 2
t = 0 kan niet
t = 2 geeft het punt (4, ln3)
       
  b. de helling moet dan 1 zijn, dus  y'/x'= 1  dus  y' = x'  
    y '= 1/(t² - 1) • 2t  en  x' = t(t - 2)/(t-1)²
2t(t - 1)2 = t(t - 2)(t2 - 1)
2(t - 1)2 = (t - 2)(t2 - 1)
2(t2 - 2t + 1) = t3 - t - 2t2 + 2
2t2 - 4t + 2 = t3 - t - 2t2 + 2
0 = t3 - 4t2 + 3t
0 = t (t2 - 4t + 3)
0 = t(t - 3)(t - 1)
t = 0 ∨  t = 3  ∨  t = 1
alleen t = 3 is toegestaan, en dat geeft het raakpunt  (41/2, ln8)
daar moet y = x + p doorgaan, dus  ln8 = 41/2 + p
p = ln8 - 41/2
       
  c. ln(t2 - 1) = a
t2 - 1 = ea
t2 = 1 + ea
t = √(1 + ea) ∨  t = -√(1 + ea)
     
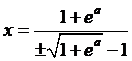    de x-coördinaat van M is het gemiddelde van deze twee:  
       
   
       
   
       
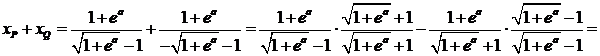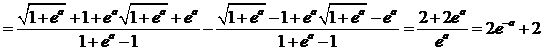    xM is de helft daarvan, dus  e-a + 1  
       
9. a. De afstand tot de assen is gelijk als x = y  of als x = -y

x = y  betekent  cos2t = cos3t  
⇒   2t = 3t (mod 2π)  ∨  2t = 2π - 3t (mod 2π)
⇒   t = 0  (mod 2π)  ∨  t = 2/5π  (mod 2/5π)

x = -y  betekent  cos 2t = -cos3t = cos(π - 3t)
⇒  2t = π - 3t  (mod 2π)  ∨  2π - 2t = π - 3t  (mod 2π)
⇒  t = 1/5π  (mod 2/5π)  ∨  t = π  (mod 2π)

Na t = 0 is het eerste tijdstip dus t = 1/5π
       
  b. y = 0,5  ⇒  cos3t = 0,5 = cos(1/3π)
⇒ 3t = 1/3π  (mod 2π)  ∨  3t = 2π - 1/3π  (mod 2π)
⇒  t = 1/9π   (mod 2/3π )  ∨  t = 5/9π  (mod 2/3π )
Tussen 0 en π geeft dat de oplossingen  t = 1/9π ,  5/9π en 7/9π
Het punt bevindt zich boven de lijn y = 0,5 als x ligt in het interval  [0, 1/9π〉 ∪ 〈5/9π, 7/9π〉
Dat is in totaal 1/3π (de eenheid in onbekend)
       
  c. snelheid v = √((x' )2 + (y ')2 ) = √((-2sin2t)2 + (-3sin3t)2) = √(4sin22t + 9cos2(3t))
plot de grafiek van v
bij t = 0,5π geeft dat v = 3.
maar het maximum zit bij t ≈ 0,56 en t ≈ 2,58 en is gelijk aan ongeveer 3,48
conclusie: de grootste snelheid wordt NIET bereikt voor t = 0,5π.
       
10. a. De afstand van P tot de oorsprong is  (Pythagoras):
OP = √(xP2 + yP2) = √( (1/2sint)2 + (sin(t + 1/3π))2 )
Voer deze formule in bij Y1 van de GR
Gebruik calc - maximum, en dat geeft dan y = 1,04
De maximale afstand is dus 1,04.
       
  b. dx/dt = x'(t) = 1/2cost
dy/dt = y'(t) = cos(t + 1/3π)
voor t = 0  geldt   dx/dt = 1/2cos0 = 1/2
voor t = 0 geldt  dy/dt = cos(0 + 1/3π) = 1/2
Dan is v = √(0,52 + 0,52) = √1/2 = 1/2√2.
       
  c. In A en B is y = 2x
Dat geeft  sin(t + 1/3π) = 2 • 1/2sint
sin(t + 1/3π) = sint
t + 1/3π = t + k2π  ∨  t + 1/3π = π - t + k2π
0 = -1/3π   ∨  2t = 2/3π+ k2π
t = 1/3π + kπ
tussen 0 en 2π geeft dat de oplossingen  t = 1/3π en  t = 11/3π
t = 1/3π  geeft  A = (1/4√3, 1/2√3)
t = 11/3π  geeft  B = (-1/4√3, -1/2√3)
       
11. a. v = √((x')2 + (y')2) = √{(-sin(t) + 2cos(2t))2  + (-2sin(t))2}
√{(-sin(X) + 2cos(2X))2  + (-2sin(X))2)
calc - maximum geeft maximale snelheid  3,6 m/s.  (bij t = 1/2π)
       
  b. y = x  geeft  cost + sin2t = 2cost
2sintcost - cost = 0
cost(2sint - 1) = 0
cost = 0  ∨  sint = 1/2
t = 1/2π  ∨  t = 3/2π  ∨ t = 1/6π  ∨  t = 5/6π
A en B horen bij   t = 1/6π  en  t = 5/6π dus de beweging duurt  2/3π  seconden.   
       
  c. P = (cost + sin(2t), 2cost)   en  Q = (cos(t + π) + sin2(t + π),  2cos(t + π)
cos(t + π) = -cost
sin2(t + π) = sin(2t + 2π) = sin(2t)
Dat geeft
P = (cost + sin(2t),  2cost)  en  Q = (-cost + sin(2t), -2cost)
Dus  Δx = 2cost  en  Δy = 4cost
De helling is dan  Δy/Δx =  2  en dat is inderdaad constant.
       
12. a. v1 = √(x1' 2 + y1'2) = √((2t + 2)2 + 16)
v2 = √(t2 + 1) 
v1 = v2  geeft dan    √((2t + 2)2 + 16) = 4√(t2 + 1)
(2t + 2)2 + 16 = 16(t2 + 1)
4t2 + 8t + 20 = 16t2 + 16
12t2 - 8t - 4 = 0
t = 1  ∨  t = -1/3
Alleen t = 1 voldoet.
       
  b. P1 = (t2 + 2t, 4t)  en P2 = (4t, 2t2)
De helling daartussen is:
(2t²- 4t)/(4t - t² - 2t) =  2t(t - 2)/t(2 - t) = -2 
Waarbij dat wegdelen aalleen mag als  t niet 0 of 2 is.
       
  c. P2 = (4t, 2t2)
lijn met helling -2 door P2 :   2t2  = -2 • 4t + b geeft  b = 2t2 + 8t
de lijn is dan  y = -2x + 2t2 + 8t
y = 0  geeft  0 = -2 • 3 + 2t2 + 8t
2t2 + 8t - 6 = 0
t2 + 4t - 3 = 0
t = (-4 ± √28)/2 = -2 ± √7
Alleen de plus-oplossing voldoet, dus t =  -2 + √7
       

© h.hofstede (h.hofstede@hogeland.nl)