© h.hofstede (h.hofstede@hogeland.nl)

       
1. a. sin(x - 1/6π) = sinx
x - 1/6π = x + k2π  ∨   x - 1/6π = π - x + k2π  
- 1/6π = k2π   ∨  2x = 7/6π + k2π
x = 7/12π + kπ
Binnen [0, 2π] geeft dat de oplossingen  {7/12π, 17/12π}
       
  b. cos(x) = cos(x + 1/4π)
x = x + 1/4π + k2π  ∨   x = 2π - (x + 1/4π) + k2π
 1/4π = k2π  ∨   2x = 13/4π + k2π
x = 7/8π + kπ
Binnen [0, 2π] geeft dat de oplossingen  {7/8π, 17/8π}
       
  c. cos(2x) = cos(x + 1)
2x = x + 1 + k2π   ∨   2x = 2π - (x + 1) + k2π
x = 1 + k2π  ∨  3x = 2π - 1 + k2π
x = 1 + k2π  ∨  x = 2/3π - 1/3 + k2/3π
Binnen [0, 2π] geeft dat de oplossingen  {1, 2/3π - 1/3,  4/3π - 1/3,  2π - 1/3}
       
  d. cos(x + π) - cos2x = 0 
cos(x + π) = cos2x 
x + π = 2x + k2π  ∨  x + π = 2π - 2x + k2π
-x = -π + k2π  ∨  3x = π + k2π
x = π + k2π  ∨   x = 1/3π + k2/3π
Binnen [0, 2π] geeft dat de oplossingen  {π, 1/3π, 5/3π}
       
  e. sin(x + 1/4π) = sin(3x - 1/3π)
x + 1/4π = 3x - 1/3π + k2π  ∨  x + 1/4π = π - (3x - 1/3π) + k2π
-2x = -7/12π + k2π  ∨  4x = 13/12π + k2π
x = 7/24π + kπ  ∨   x = 13/48π + k1/2π
Binnen [0, 2π] geeft dat de oplossingen  {7/24π, 31/24π, 13/48π, 37/48π, 61/48π, 85/48π}
       
  f. sin(1/2x) = sin(π - x)
1/2x = π - x + k2π   ∨  1/2x = π - (π - x) + k2π
11/2x = π + k2π  ∨   -1/2x = k2π
x = 2/3π + k4/3π  ∨    x = k4π
Binnen [0, 2π] geeft dat de oplossingen {0, 2/3π, 2π}
       
  g. sin(x + 4) = sin(2 - x)
x + 4 = 2 - x + k2π  ∨  x + 4 = π - (2 - x) + k2π
2x = -2 + k2π  ∨   4 = π - 2 + k2π
x = -1 + kπ
Binnen [0, 2π] geeft dat de oplossingen  {-1 + π, -1 + 2π}
       
  h. cos(2x + 2/3π) = cos(1/6π - x)
2x + 2/3π = 1/6π - x + k2π  ∨  2x + 2/3π = 2π - (1/6π - x) + k2π
3x = -1/2π + k2π  ∨   x = 7/6π + k2π
x = -1/6π + k2/3π   ∨   x = 7/6π + k2π
Binnen [0, 2π] geeft dat de oplossingen  {1/2π, 7/6π, 11/6π}
       
2. sin(1/6π) = sin(p + 1/6p)
1/6π = p + 1/6π + k2π   ∨   1/6π = π - (p + 1/6π) + k2π
p = k2π  ∨   p = 4/6π + k2π
mogelijkheden zijn:  {0, 2π, 4π, ...} en {2/3π, 22/3π, 42/3π, ...}
       
3. cosx = cosy  geeft  x = y + k2π  ∨   x = 2π - y + k2π
Dat geeft de lijnen;
y = x,  y = x + 2π,  y = x + 4π, ....  allemaal, lijnen evenwijdig aan y = x
y = -x, y = -x + 2π,  y = -x + 4π, .....allemaal lijnen evenwijdig aan y = -x
Samen geeft dat figuur e, waarbij de verticale afstand tussen al die evenwijdige lijnen dus gelijk is aan 2π.
       
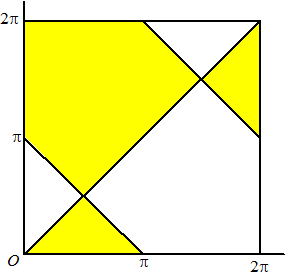
4. voor de grenslijnen geldt:  sinx = siny
y = x + k2π  ∨ y =  π - x + k2π
Dat geeft de lijnen hieronder en in de gele gebieden geldt de ongelijkheid.
       
 

       

© h.hofstede (h.hofstede@hogeland.nl)