|
|||||
| 1. | a. | cos(2α) = cos2α - sin2α = 1 - sin2α - sin2α = 1 - 2sin2α | |||
| b. | cos(2α) = cos2α - sin2α = cos2α - (1 - cos2α) = cos2α - 1 + cos2α = 2cos2α - 1 | ||||
| c. | (sinα +
cosα)2
= (sinα + cosα)(sina + cosa) = sin2α + sinαcosa + cosαsinα + cos2α = sin2α + cos2α + 2sinαcosα = 1 + 2sinαcosα = 1 + sin2α |
||||
| 2. | a. | sin(3α)
= sin(2α + α) = sin2αcosα + cos2αsinα = 2sinαcosαcosα + (1- 2sin2α)sinα = 2sinαcos2α + sinα - 2sin3α = 2sinα(1 - sin2α) + sinα - 2sin3α = 2sinα - 2sin3α + sinα - 2sin3α = 3sinα - 4sin3α |
|||
| b. | sin(4α)
= sin(2α + 2α) = sin2αcos2α + cos2αsin2α = 2sin2αcos2α = 2 2sinαcosα (cos2α - sin2α) = 4sinαcosα cos2α - 4sinαcosα sin2α = 4sinαcos3α - 4sin3αcosα |
||||
| c. | sin(4α)
= sin(2α + 2α) = sin2αcos2α + cos2αsin2α = 2sin2αcos2α = 2sin2α (1 - 2sin2α) |
||||
| 3. | a. | sin(1/6π)
= sin(2 1/12π) = 2sin(1/12π) cos(1/12π) = 1/2 4sin2(1/12π) cos2(1/12π) = 1/4 4sin2(1/12π) (1 - sin2(1/12π)) = 1/4 noem sin2(1/12π) = p 4p(1 - p) = 1/4 16p - 16p2 - 1 = 0 16p2 - 16p + 1 = 0 p = (16 ±√(256 - 64))/32 = (16 ± √192)/32 = (16 ± 8√3)/32 = 1/2 ± 1/4√3 omdat p kleiner dan 0,25 moet zijn (immers sin2(1/6π) = 0,25) is p = 1/2 - 1/4√3 sin2(1/12π) = 1/2 - 1/4√3 sin(1/12π) = √(1/2 - 1/4√3) (alleen positief omdat de sinus van 1/12π positief is) |
|||
| b. | cos(1/4π) = cos(2 1/8π) = 2cos2(1/8π) - 1 = 1/2√2 2cos2(1/8π) = 1 + 1/2√2 cos2(1/8π) = 1/2 + 1/4√2 cos(1/8π) = √(1/2 + 1/4√2) |
||||
| c. | cos(1/8π) = cos(2 1/16π) = 2cos2(1/16π) - 1 = √(1/2 + 1/4√2) 2cos2(1/16π) = 1 + √(1/2 + 1/4√2) cos2(1/16π) = 1/2 + 1/2√(1/2 + 1/4√2) cos(1/16π) = √(1/2 + 1/2√(1/2 + 1/4√2)) |
||||
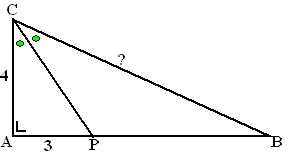
| 4. | Noem de groene hoek
x in driehoek APC: is PC = 5 (Pythagoras) Dan is cosx = 4/5 in driehoek ABC: cos2x = 4/BC cos2x = 2cos2x - 1 = 2 (4/5)2 - 1 = 7/25 Dus is 4/BC = 7/25 BC = 100/7 |
 |
|||
| 5. | a. | Vermenigvuldig alles
met 2sinx: (sinx ≠ 0) 2sin3x + sin2x = 2sinx 2sin3x + 2sinxcosx - 2sinx = 0 2sinx (sin2x + cosx - 1) = 0 sin2x + cosx - 1 = 0 (want sinx ¹ 0) 1 - cos2x+ cosx - 1 = 0 cosx - cos2x = 0 cosx(1 - cosx) = 0 cosx = 0 ∨ cosx = 1 x = 1/2π ∨ x = 11/2π ∨ x = 0 ∨ x = 2π Die laatste twee vallen af, want dan is sinx = 0, dus blijft over x = 1/2π ∨ x = 11/2π. |
|||
| b. | cos2x - sinx = 0 1 - 2sin2x - sinx = 0 noem sinx = p -2p2 - p + 1 = 0 ABC- formule: p = (1 ±√(1 + 8))/-4 = (1 ± 3)/-4 = 1/2 of -1 sinx = 1/2 ∨ sinx = -1 x = 1/6π ∨ x = 5/6π ∨ x = 11/2π |
||||
| 6. | cosinusregel op twee
manieren: 42 = 52 + 62 - 2 5 6 cosα en daaruit volgt cosα = 9/12 62 = 42 + 52 - 2 4 5 cosγ en daaruit volgt cosγ = 1/8 2 (9/12)2 - 1 = 1/8 Dus cosγ = 2 cos2α - 1 Dan is γ = 2α |
||||
| 7. |
|
||||
| 8. | a. | Y1 = 2cos(X) en Y2 = cos(2X) Intersect geeft X = 1,95 ∨ X = 4,34 |
|||
| b. | 2cosx = cos(2x) 2cosx = 2cos2x - 1 noem cosx = p 2p2 - 2p - 1 = 0 ABC-formule: p = (2 ±√(4 + 8))/4 = (2 ±√12)/4 = 1,366 of -0,366 cosx = 1,366 kan niet. cosx = -0,366 x = cos-1(-0,366) = 1,95 ∨ x = 2π - 1,95 = 4,34 |
||||
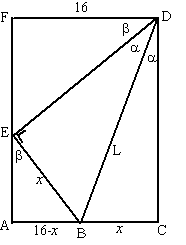
| 9. | Zie de figuur hiernaast. β = 90 - 2α (bij hoek D) ∠DEF = 90 - β dus is ∠AEB = β In driehoek AEB: sinb = sin(90 - 2α) = cos(2α) = (16-x)/x = 16/x - 1 cos(2α) = 2cos2α - 1, dus 16/x - 1 = 2cos2α - 1 2cos2α = 16/x dus cos2α = 8/x dus x = 8/cos2α In driehoek DBC: sinα = x/L dus L = x/sinα Samen geeft dat L = 8/cos2α sinα = 8/(1 - sin2α)sinα = 8/(sinα - sin3α) |
|
|||
| 10. | cos(4x) = cos(2 2x) = 2cos2(2x) - 1 = 2 (2cos2x - 1)2 - 1 = 2 (4cos4x - 4cos2x + 1) - 1 = 8cos4x - 8cos2x + 1 cos(4x) + 11cos2x = 0 8cos4x - 8cos2x + 1 + 2cos2x = 0 8cos4x - 6cos2x + 1 = 0 noem nu cos2x = p 8p2 - 6p + 1 = 0 ABC-formule: p = (6±√(36-32))/16 = (6 ± 2)/16 = 1/2 of 1/4 cos2p = 1/2 ∨ cos2p = 1/4 cosp = 1/2√2 ∨ cosp = -1/2√2 ∨ cosp = 1/2 ∨ cosp = -1/2 p = 1/4π ∨ p = 13/4π ∨ p = 3/4π ∨ p =11/4π ∨ p = 1/3π ∨ p = 12/3π ∨ p = 2/3π ∨ p = 11/3π |
||||
| 11. | Nulpunten: sin2x - 2sinx = 0 2sinxcosx - 2sinx = 0 2sinx(cosx - 1) = 0 sinx = 0 ∨ cosx = 1 x = 0 ∨ x = π ∨ x = 2π Extremen: afgeleide moet nul zijn. f ' = 2cos2x - 2cosx = 0 2(2cos2x - 1) - 2cosx = 0 4cos2x - 2 - 2cosx = 0 2cos2x - cosx - 1 = 0 noem nu cos = p 2p2 - p - 1 = 0 ABC-formule: p = (1 ±√(1 + 8))/4 = (1 ± 3)/4 = 1 of -1/2 cosx = 1 ∨ cosx = -1/2 x = 0 ∨ x = 2π ∨ x = 2/3π ∨ x = 11/3π De extremen zijn dan (0, 0) en (2/3π, -3/2√3) en (11/3π, 3/2√3) en (2π, 0) |
||||
| 12. | a. | 3sinx = 1/cosx 3sinxcosx = 1 11/2 2sinxcosx = 1 11/2 sin2x = 1 sin2x = 2/3 2x = sin-1(2/3) = 0,73 + k2π ∨ 2x = π - 0,73 = 2,41 + k2π x = 0,36 + kπ ∨ x = 1,21 + kπ In [0,1/2π] geeft dat de oplossingen {0.36, 1.21} Dat geeft de punten (0.36, 1.07) en (1.21, 2.80) |
|||
| b. | asinx = 1/cosx asinxcosx = 1 1/2a 2sinxcosx = 1 1/2a sin2x = 1 sin2x = 2/a Dat heeft geen oplossing als 2/a > 1 of 2/a < -1 Dat betekent dat a < 2 of a > -2 dus a in het interval 〈-2, 2〉 |
||||
| 13. | sin2x + cos2x = a(sinx + cosx) 2sinxcosx + cos2x - sin2x = a(sinx + cosx) Deel alles door cosx; 2sinx + cosx - sin²x/cosx = a(sinx/cosx + 1) Maar sinx/cosx = tanx = 2, dus dat wordt; 2sinx + cosx - 2sinx = a(2 + 1) cosx = 3a Omdat -1 ≤ cosx ≤ 1 geldt dus -1/3 ≤ a ≤ 1/3 |
||||
| 14. |
√(4 - 7sin2x) = cosx -
sinx 4 - 7sin2x = (cosx - sinx)2 4 - 7sin2x = cos2x - 2sinxcosx + sin2x 4 - 7sin2x = 1 - sin2x 3 = 6sin2x sin2x = 1/2 2x = 1/6π + k2π ∨ 2x = 5/6π + k2π x = 1/12π + kπ ∨ x = 5/12π + kπ |
||||
|
© h.hofstede (h.hofstede@hogeland.nl) |
|||||