|
|||||
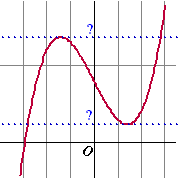
| 1. | Zie de grafiek
hiernaast. Tussen beide blauwe lijnen zijn er drie snijpunten en dus drie oplossingen. Het is dus zaak het maximum en het minimum van de grafiek te vinden. Daar is de afgeleide nul. f '(x) = 3x2 - 6 = 0 3x2 = 6 x2 = 2 x = √2 of x = -√2. |
|
|||
| x =
√2 geeft y = x3 - 6x + 8
= (√2)3 - 6√2
+ 8 = 2√2 - 6√2
+ 8 = 8 - 4√2 = 2,343 x = -√2 geeft y = x3 - 6x + 8 = (-√2)3 + 6√2 + 8 = -2√2 + 6√2 + 8 = 8 + 4√2 = 13,657 Voor p tussen 2,343 en 13,657 zijn er drie snijpunten dus 3 oplossingen. |
|||||
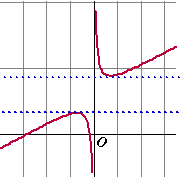
| 2. | Zie de figuur
hiernaast. Er zijn twee oplossingen zolang de y-coördinaat maar niet tussen de beide blauwe lijnen ligt. Het is dus zaak het maximum en het minimum van de grafiek te vinden. Daar is de afgeleide nul. f '(x) = 2 - 1/x2 = 0 1/x2 = 2 x2 = 1/2 x = √1/2 = 0,707 ∨ x = -√1/2 = -0,707. |
|
|||
| x = 0,707
geeft y = 8,828 x = -0,707 geeft y = 3,172 Er zijn twee oplossingen voor p > 8,828 en p < 3,172 |
|||||
| 3. | (x²
- 8)/(4x + 4) = p x2 - 8 = p(4x + 4) x2 - 4px - 8 - 4p = 0 x2 - 4px - (8 + 4p) = 0 De twee oplossingen vind je met de ABC-formule: x = (4p ±√(16p² + 4 • 1 • (8 + 4p))/2 x = 2p ± 1/2 • √(16p2 + 4(8 + 4p)) De afstand tussen die twee punten is √(16p2 + 4(8 + 4p)) = 8 16p2 + 4(8 + 4p) = 64 16p2 + 16p - 32 = 0 p2 + p - 2 = 0 (p - 1)(p + 2) = 0 p = 1 ∨ p = -2 |
||||
| 4. | a. | f(x)
= 0 3√(x3 + 3x2 + 2x) = 0 x3 + 3x2 + 2 = 0 x(x2 + 3x + 2) = 0 x(x + 2)(x + 1) = 0 x = 0 ∨ x = -2 ∨ x = -1 |
|||
| b. | De waarde van p moet tussen het maximum en het minimum
van de grafiek liggen. Dat kan met de GR m,et de optie calc - maximum/minimum of algebraïsch zó: f '(x) = 0 1/3 • (x3 + 3x2 + 2x)-2/3 • (3x2 + 6x + 2) = 0 3x2 + 6x + 2 = 0 ABC-formule: x = (-6 ±√12)/6 x = -0,42 ∨ x = -1,58 y = 0,727 ∨ y = -0,727 Dus -0,727 < p < 0,727 |
||||
|
© h.hofstede (h.hofstede@hogeland.nl) |
|||||