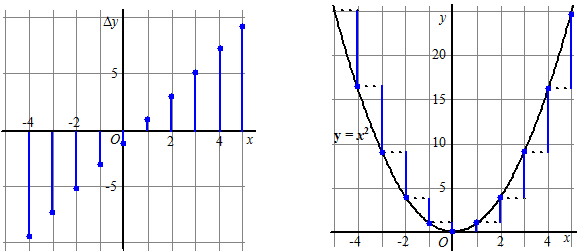
toenamendiagram kwadratische functie

© h.hofstede (h.hofstede@hogeland.nl)

Het toenamendiagram van een kwadratische functie.

Je ontdekt iets aparts als je het toenamendiagram van een kwadratische functie bekijkt. Met een kwadratische functie bedoel ik: "Een formule met als hoogste macht van x een kwadraat". Er mogen behalve x² dus ook nog best stukken met x of losse getallen in de formule staan.
In de meest algemene vorm zal zo'n functie er (na vereenvoudigen een haakjes wegwerken en zo) zó uit zien:
y = ax² + bx + c (met a, b en c constante getallen)

De meest eenvoudige kwadratische functie is natuurlijk y = x² .
Laten we daar een toenamendiagram van maken:

x	-5	-4	-3	-2	-1	0	1	2	3	4	5
y	25	16	9	4	1	0	1	4	9	16	25
Δy	-	-9	-7	-5	-3	-1	1	3	5	7	9

Links zie je het toenamendiagram, rechts wat dat met de grafiek zelf te maken heeft.
Aan dat toenamendiagram zal je direct één ding opvallen hoop ik: die uiteinden liggen op een rechte lijn!!
En nou komt het aparte: dat is bij elke kwadraatformule zo!

de bolletjes van het toenamendiagram van een parabool liggen op een rechte lijn.

Het bewijs van deze alleraardigste eigenschap

De meest algemene kwadratische functie is f(x) = ax² + bx + c

Maar ga je dan één stapje naar rechts, dan wordt x dus één groter en dan krijg je de nieuwe y die daarbij hoort door voor x nu x + 1 in de formule in te vullen:

f(x + 1) = a(x + 1)² + b(x + 1) + c
   = a(x² + 2x + 1) + bx + b + c
   = ax² + 2ax + a + bx + b + c
   = ax² + bx + c + 2ax + b + c

Maar dat eerste stuk ax² + bx + c dat was de oude y
Dus dat deel 2ax + b + c dat is het deel dat er bij is gekomen, dus dat is de lengte van het stokje van het toenamendiagram.
Maar dat is een een oude bekende: y = 2ax + b + c is de vergelijking van een rechte lijn! (met hellinggetal 2a en beginpunt b + c)

Daarmee is het bewijs geleverd.