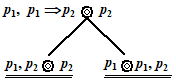© h.hofstede (h.hofstede@hogeland.nl)

Semantische Tableaus.
       
De vorige les hebben we gekeken of een bepaalde conclusie (of welke conclusie) logisch volgt uit een aantal beginformules.
Je zou dat natuurlijk altijd kunnen onderzoeken met een waarheidstabel.
Bijvoorbeeld, stel dat we ons afvragen of het volgende geldig is:
       
p1  ⇒ p2
p3  ⇒ p2
p1 ∨  p3
_______
p2
       
Ofwel:  volgt die onderste uit de bovenste drie beweringen?
De waarheidstabel daarbij zou er zó uitzien:
       

       
En nu moet je controleren bij het geval dat alle drie de voorwaarden waar zijn (dat zijn de enen in de rechthoek) of daar de conclusie (de p2-kolom) ook elke keer een 1 geeft.
Dat is inderdaad zo, dus deze gevolgtrekking klopt.

Maar dit is een nogal inefficiënte controlemanier. De tabellen worden bij meer p's snel groter, en bovendien wordt het grootste gedeelte ervan toch niet gebruikt. We waren alleen geïnteresseerd in de enen uit de kolom met de rechthoek, de rest van de tabel deed er eigenlijk niet toe.

Als je er nog even langer over nadenkt zul je snappen dat we eigenlijk alleen geïnteresseerd waren in de vraag of er een horizontale lijn in de tabel zou verschijnen met in de rechthoekkolom een 1 en in de conclusiekolom (p2)  een 0. We zochten eigenlijk een tegenvoorbeeld.....
De methode van de semantische tableaus (door de Nederlandse Evert Willem Beth, 1955) doet dat op een redelijk eenvoudige manier.
   
De methode.

Je hebt een aantal formules  α1, α2, α3, .... (het mogen ook enkelvoudige premissen pi zijn),
en je hebt een eindconclusie Ω.
De vraag is nu:  is er een tegenvoorbeeld voor:   (α1 ∧ α2 ∧ α3 ∧ ...)  ⇒ Ω   te vinden?

We noteren dit voor het gemak als  α1, α2, α3, ... ⊚ Ω.  Ik gebruik een soort dikke stip (Beth noemde het een knoop) voor de implicatiepijl waar alles om draait, anders komen we misschien in de war met andere implicatiepijlen in de beginformules αi.

Beth's truc was om deze vraag stap voor stap terug te brengen tot steeds eenvoudiger vragen, net zolang totdat de vragen zó eenvoudig waren geworden dat ze in één oogopslag te beantwoorden waren.
 
minivraagje1:  geldt  p1, p2 ⊚ p1 ?
Natuurlijk, want het kan nooit zo zijn dat p1 = 1 en p2 = 1 en toch p1 = 0 
Ik noteer hier nogal slordig p1 = 1  in plaats van  W(p1) = 1: "de waarde van p1 is 1".
Dat zal wel geen misverstanden geven.

minivraagje 2:  geldt  p1, p2 ⊚ p3  ?
Natuurlijk niet; neem als tegenvoorbeeld  p1 = 1 en p2 = 1 en p3 = 0

minivraagje 3:   geldt   p1,  p1 ⇒ p2  ⊚ p2  ?
Als er een tegenvoorbeeld te vinden is, dan moet er dus een geval zijn waarbij p1 en p1 ⇒ p2 beiden 1 zijn,
en tegelijk p2 = 0
Merk op dat bij een tegenvoorbeeld  links van de knoop alles waarde 1 heeft, en rechts van de knoop 0.

Hier komt ons systeem in werking.

Voor de formule  p1 ⇒ p2 zijn er twee mogelijkheden om waar te zijn (= waarde 1 te hebben),  namelijk p1 = 0  of  p2 = 1.
Daarom gaan we een boom maken, die zich vanaf deze knoop splitst in deze twee mogelijkheden. Daarbij schrijven we elke keer de formules die voor dit tegenvoorbeeld waar moeten zijn rechts van de knoop, en de formules die voor een tegenvoorbeeld onwaar moeten zijn links. Dat ziet er zó uit:
       

       
Links staat het geval p2 = 1, rechts staat het geval p1 = 0. De streep onder beide takken betekent dat die takken sluiten. Dat betekent dat je ze niet verder hoeft te onderzoeken omdat ze niet goed zijn. Je ziet dat zodra één formule links én rechts van de knoop voorkomt; een formule kan immers nooit 1 en 0 zijn? 
Van dit boompje hier sluiten alle takken dus geen enkel tegenvoorbeeld was goed, dus het antwoord was  JA, dit geldt!
       
Nog een paar semantische tableaus (sla ze vooral over als je het al snapt):
       

       
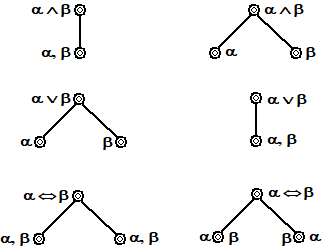
Logisch natuurlijk dat een ¬ p aan de andere kant van de knoop tevoorschijn komt als een  p.
Je ziet dat de linkerboom niet sluit, dus er is een tegenvoorbeeld te vinden, dus het antwoord is NEE; de conclusie volgt niet uit de formules.
De rechterboom sluit wel; daar is dus geen tegenvoorbeeld te vinden, dus daar is het antwoord JA; de conclusie volgt inderdaad uit deze formules.

Als er alleen maar een eindconclusie is gegeven en geen premissen waar die uit moet volgen, dan zet je om een tegenvoorbeeld te vinden niets links van de knoop en deze hele conclusie rechts (moet voor een tegenvoorbeeld immers onwaar worden).

Voorbeeld:

       
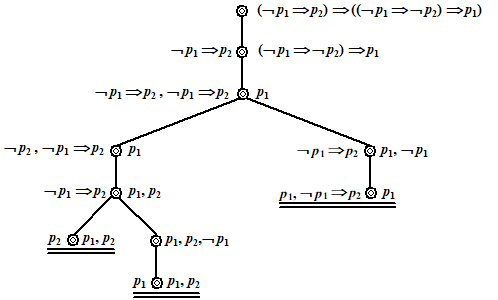
In het begin staat er nu een implicatie aan de rechterkant, dus een implicatie die niet waar is. Nou staat er in de waarheidstabel dat  p1 ⇒ p2 alleen niet waar is als p1 waar is, en p2 niet waar. In zo'n geval moet dus p1 naar de linkerkant van de boom worden verplaatst en p2 rechts blijven staan. Dat is hierboven in de eerste stap ook gebeurd.

Je zou dit nog wat efficiënter kunnen noteren door formules niet steeds van boven naar beneden in het tableau te herhalen. Je kunt ook afspreken dat formules aan hun kant van de boom naar beneden toe van kracht blijven.

De verplaatsregels voor de andere connectieven:
       

       
       

© h.hofstede (h.hofstede@hogeland.nl)