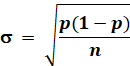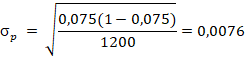|
|||||||||||||
| Van Steekproef naar Populatie. | |||||||||||||
| Ik moet eerlijk
zeggen, die vorige les (van populatie naar steekproef), daar heb je niet
zo heel veel aan, want je kent meestal tóch de gegevens van de populatie
niet. Als dat wel zo zou zijn, waarom zou je dan nog een "onderzoek"
willen doen? Deze les wordt nuttiger. We gaan bekijken in hoeverre resultaten van een steekproef iets zeggen over de populatie. De andere kant op dus. En dat is nou juist het doel van de meeste onderzoeken. Laat één ding vooraf volkomen duidelijk zijn, misschien wel HET principe van deze les: |
|||||||||||||
|
|||||||||||||
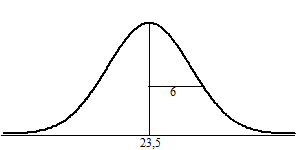
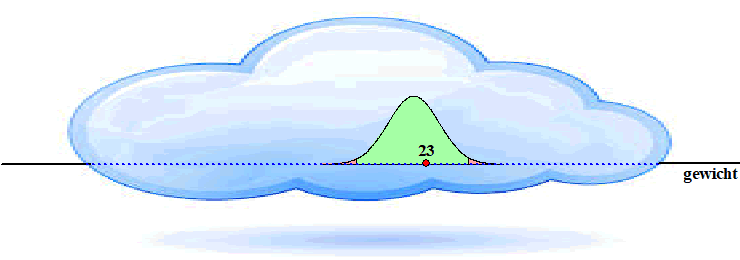
| Stel dat je in een
(verantwoord) onderzoek hebt gevonden dat het gemiddelde gewicht van
zesjarige kinderen in een steekproef die je hebt gehouden gelijk is aan
23 kg (met een standaarddeviatie van 6 kg). Dan lijkt het een redelijke
veronderstelling om te zeggen dat van alle kinderen in Nederland het
gemiddelde gewicht gelijk zal zijn aan ongeveer 23 kg. Hoe groter je
steekproef, hoe betrouwbaarder dat getal zal zijn. Maar je weet het nooit helemaal zeker! Overschrijdingskans. Je vermoedt dat het gemiddelde gewicht voor heel Nederland ongeveer gelijk zal zijn aan G ≈ 23 met een standaarddeviatie van 6 kg. Maar als dat niet zo is, en G is bijvoorbeeld 23,5 kg met een standaarddeviatie van 6 kg, dan ziet de gewichtsverdeling er in werkelijkheid zó uit: |
|||||||||||||
|
|
|||||||||||||
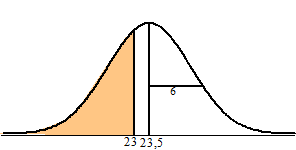
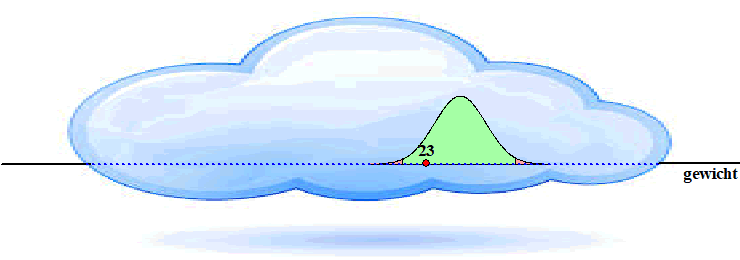
| Ook dan zou jouw
steekproef dus best een waarde van 23 kunnen opleveren. Of zelfs nog
lager. Dat is natuurlijk wel een afwijking van de 23,5 maar niet een al
te grote. Geef toe: Het zou zelfs heel toevallig zijn als jouw
steekproef PRECIES 23,5 zou opleveren! Kortom: een afwijking zal
vaak voorkomen, maar een al te grote afwijking niet. Daarom gebruiken we vanaf nu het begrip "overschrijdingskans": |
|||||||||||||
|
|||||||||||||
| We kunnen de kans op die overschrijdingskans in ons geval natuurlijk makkelijk uitrekenen. Het is de oppervlakte van het gekleurde gebied hieronder (en die is normalcdf(0, 23, 23.5, 6) = 47%). | |||||||||||||
|
|
|||||||||||||
|
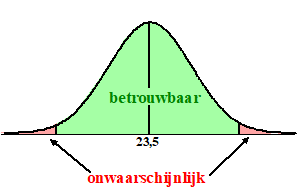
Betrouwbaarheidsinterval. Bij het maken van een schatting voor een gemiddelde in een populatie gaan we voortaan gebruik maken van het begrip "betrouwbaarheid". Stel dat we kiezen voor een betrouwbaarheid van 95%. Dan noemen we de metingen die in een gebied van 95% rond het midden liggen "betrouwbaar". De buitenste 5% van de klokvorm noemen we "onwaarschijnlijk". De metingen in het groene gebied hieronder zijn dus "betrouwbaar" en de metingen in het rode gebied zijn "onwaarschijnlijk". |
|||||||||||||
|
|
|||||||||||||
| Bij een normale verdeling ligt 95% van alle metingen tussen μ - 2σ en μ + 2σ dus dat zijn de grenzen van het groene gebied. | |||||||||||||
| Terug naar ons probleem. | |||||||||||||
| Wat was het probleem
ook al weer? Nou, stel dat we in een steekproef een gemiddelde van 23
hebben gemeten, wat kunnen we dan over het gemiddelde van de hele
populatie zeggen? Ofwel: ergens in deze mist ligt een klokvorm verscholen, en wij hebben als enige gegeven een gemeten gemiddelde van 23. |
|||||||||||||
|
|
|||||||||||||
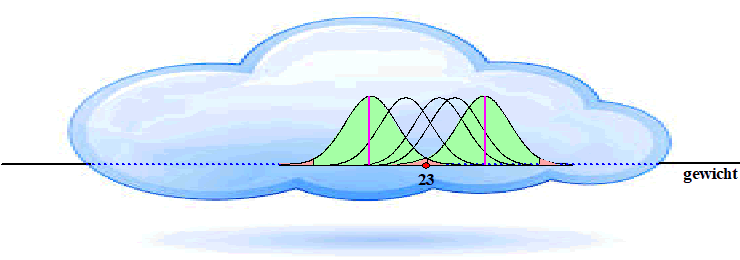
| Waar oh waar ligt het
gemiddelde van de werkelijke klokvorm........????? |
|||||||||||||
| Laten we ezeltje prik gaan spelen..... |
|
||||||||||||
|
|
|||||||||||||
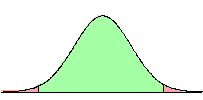
| Jij moet de klokvorm hiernaast ergens op die getallenlijn neerleggen,
waarbij de enige voorwaarde is dat onze meting van 23 kg een betrouwbare
meting moet zijn. Bijvoorbeeld zó: |
 |
||||||||||||
|
|
|||||||||||||
| Het werkelijke
gemiddelde lijkt nu iets links van 23 te liggen, maar 23 is een
betrouwbare meting want ligt in het groene gebied van deze klokvorm.. Of zó: |
|||||||||||||
|
|
|||||||||||||
| Nu ligt het
werkelijke gemiddelde een stuk rechts van 23, maar 23 is nog steeds een
betrouwbare meting. OK, geen kinderspelletjes neer; laten we direct aangeven wat de uiterste grenzen voor het gemiddelde van de werkelijke klokvorm kunnen zijn: |
|||||||||||||
|
|
|||||||||||||
| Alle gemiddeldes
tussen die twee paarse strepen zijn mogelijk als onze meting een
betrouwbare meting is. Dat gebied waarin het werkelijke gemiddelde kan liggen noemen we het 95%-betrouwbaarheidsinterval. |
|||||||||||||
|
|||||||||||||
| Natuurlijk kun je ook
andere betrouwbaarheden kiezen. Zo zou een 68% betrouwbaarheidsinterval gelijk zijn aan [x - σ, x + σ] want volgens de vuistregels van de normale verdeling ligt 68% van de metingen tussen die grenzen. En je kunt ook best 99%-betrouwbaarheidsintervallen of 90%-betrouwbaarheidsintervallen berekenen, maar dat moet dan wel met "normalcdf" knop van je GR. Die weet ik niet uit mijn hoofd. |
|||||||||||||
|
Wat stelt het voor? We hebben gevonden dat, als het gemiddelde in het betrouwbaarheidsinterval ligt, onze meting een betrouwbare meting is. Maar natuurlijk HOEFT onze meting niet een betrouwbare meting te zijn; het kan een toevallige uitschieter zijn. In dat geval zou het werkelijke gemiddelde NIET in het betrouwbaarheidsinterval liggen. Hoe groot is de kans dat dat zo is? Nou die is uiteraard precies 5%, want de kans op een onwaarschijnlijke meting was immers 5%. Ofwel: het 95%-betrouwbaarheidsinterval is het gebied waarvan we, aan de hand van onze steekproef, met 95% zekerheid kunnen zeggen dat het werkelijke gemiddelde zich daarbinnen zal bevinden.
De standaarddeviatie. |
|||||||||||||
|
|||||||||||||
| voorbeeld Een antropoloog meet de lengtes van een steekproef van 100 vrouwen uit een zekere populatie en vindt een gemiddelde van 179 cm met een standaarddeviatie van 18 cm. Voor een gemiddelde van 100 vrouwen geldt dan een normale verdeling met σ = 18/√100 = 1,8 179 + 2 • 1,8 = 182,6 en 179 - 2 • 1,8 = 175,4 Het 95%-betrouwbaarheidsinterval voor μ is dus ongeveer [175.4, 182.6]. Een analogie Dit is in feite wat er in het vorige verhaal gebeurd is: |
|||||||||||||
|
|
|||||||||||||
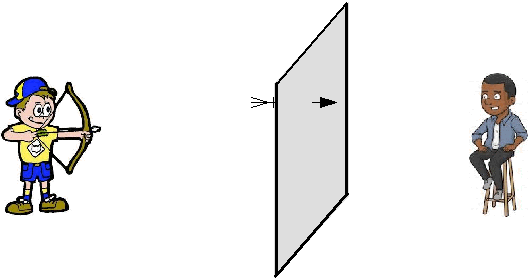
| Een statisticus zit
aan de achterkant van een scherm waarop aan de voorkant een roos is
getekend. Hij weet dat de boogschutter in 95% van de gevallen hoogstens 10 cm van de roos afwijkt. Hij ziet één pijl door het scherm steken, en moet nu raden waar de roos is getekend....... Als hij dan rondom die ene pijl een cirkel met straal 10 cm tekent heeft hij 95% kans dat de roos inderdaad binnen die cirkel ligt. Die cirkel is zijn 95%-betrouwbaarheidsinterval. Om de analogie nog even vast te houden: er zijn twee manieren voor de statisticus om de nauwkeurigheid van zijn schatting te vergroten. 1. De straal van de cirkel groter maken. Dat zou overeenkomen met het vergroten van het betrouwbaarheidsinterval. Een 99%-betrouwbaarheidsinterval zal groter zijn dan een 95% interval. 2. Een schutter te kiezen die nauwkeuriger kan schieten! Dat komt overeen met het vergroten van de steekproef. |
|||||||||||||
| Proporties meten | |||||||||||||
| Natuurlijk kun je in
plaats van een gemiddelde te meten ook best een percentage meten. Dat
noemen we een proportie. Tenminste als je dat percentage als een kommagetal tussen 0 en 1 noteert. Je zou bijvoorbeeld kunnen meten hoeveel procent van de eerstejaarsstudenten na een jaar nog thuis woont. Stel dat je een enquête onder 200 eerstejaars studenten houdt waarvan er 70 nog thuis blijken te wonen. Dat is 35%. Dus zou je willen beweren: "Van de eerstejaarsstudenten woont 35% nog thuis" Maar ja.... Hoe betrouwbaar is die 35%.......? Precies dezelfde vraag als hierboven : Hoe kun je een steekproefmeting van 35% vertalen naar een populatiebewering? De bewering hierboven is hetzelfde als: "De kans dat een student nog thuis woont is 0,35" Daarbij hoort dus een binomiale verdeling met n = 200, p = ? en k = 70. De berekening van het 95%-betrouwbaarheidsinterval voor p gaat precies hetzelfde als bij de normale verdeling hierboven. Het enige verschil is dat we nu met staafjesdiagrammen te maken hebben in plaats van vloeiende klokvormen en dat de berekeningen nu via binomcdf(n, p, k) gaan in plaats van normaldcdf. |
|||||||||||||
| Voorbeeld. | |||||||||||||
| In een onderzoek onder 1200 middelbare scholieren zeggen 90 van hen wel eens te blowen. Welk 95%-betrouwbaarheidsinterval voor de hele populatie hoort daarbij? |
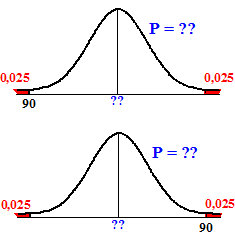 |
||||||||||||
| Bij deze vraag horen
beide plaatjes hiernaast (eigenlijk staafjes in plaats
van een vloeiende klokvorm). Het gaat erom hoe groot de blauwe
populatieproporties P maximaal en minimaal mogen zijn zodat de
overschrijdingskans bij onze meting van 90 minimaal 5% is. bovenste plaatje: binomcdf(1200, X, 90) = 0,025 geeft X = P = 0,091 onderste plaatje: binomcdf(1200, X, 89) = 0,975 geeft X = P = 0,061 Het betrouwbaarheidsinterval is [0.061, 0.091] |
|||||||||||||
| Conclusie van dit onderzoek: | |||||||||||||
|
|
|||||||||||||
|
Maar Wacht! We kennen toch de
standaardafwijking van de biomiale verdeling? Waarom dan zo moeilijk doen met die binomcdf? Tja, dat klopt eigenlijk wel. Die standaardafwijking is gelijk aan: |
|||||||||||||
|
|||||||||||||
| De afleiding en
uitleg daarvan kun je in
deze les
vinden. In het voorbeeld van de blowende middelbare scholieren zou dat direct geven: n = 1200 en p = 90/1200 = 0,075 |
|||||||||||||
|
|
|||||||||||||
| Dat geeft direct het
interval [0.075 - 2 • 0,0076 ; 0.075 + 2 • 0,076] Dat is [0.0598 , 0.0902] |
|||||||||||||
| OPGAVEN | |||||||||||||
| 1. | Als je de grootte van een steekproef laat toenemen, zal de grootte van het 95%-betrouwbaarheidsinterval dan afnemen of toenemen? Leg uit! | ||||||||||||
|
|||||||||||||
| 2. | De reactietijd van
180 gamers is getest en daaruit bleek een gemiddelde van 0,78 sec met
een standaarddeviatie van 0,15 sec. Geef het 95%-betrouwbaarheidsinterval dat uit dit onderzoek volgt. |
||||||||||||
|
|||||||||||||
| 3. | Een onderzoek onder
300 Vlamingen leverde op dat 76% van hen tegen de komst van nog meer
asielzoekers was. Geef een 95%-betrouwbaarheidsinterval voor het werkelijk percentage Vlamingen dat tegen de komst van nog meer asielzoekers was. |
||||||||||||
|
|||||||||||||
| 4. | Na het centraal
examen wiskunde levert een steekproef van het CITO onder 88 deelnemers
op, dat hun gemiddelde een 6,4 is met een standaarddeviatie van
0,7. Geef in drie decimalen nauwkeurig een 95%-betrouwbaarheidsinterval voor het werkelijk gemiddelde in heel Nederland. |
||||||||||||
|
|||||||||||||
| 5. | Examenopgave Havo,
Wiskunde A, 2018. Sinds de jaren tachtig meet het Trimbos-instituut regelmatig via een enquête het gebruik van alcohol, drugs en tabak in aselecte, representatieve steekproeven onder alle leerlingen van het voortgezet onderwijs. Ook werd de leerlingen in de enquête gevraagd naar hun leeftijd (in jaren), hun geslacht (jongen, meisje), en hun schoolniveau (vmbo, havo, vwo). Aan de enquête van 2015 deden 6714 leerlingen mee in de leeftijd van 12 tot en met 16 jaar. In deze groep is onder andere gekeken naar de lifetime-prevalentie van roken. Hieronder staat wat dit begrip betekent: |
||||||||||||
|
|||||||||||||
|
|||||||||||||
|
In de tabel zie je dat van de leerlingen in de
steekproef 23%, bijna een kwart, rookt of ooit gerookt heeft. |
|||||||||||||
|
|||||||||||||
| 6. | Examenopgave Havo,
Wiskunde A, 2016. Patiënten die voor een behandeling enige tijd in een ziekenhuis worden opgenomen, lopen tijdens dit verblijf het risico een infectie te krijgen. Zo’n infectie wordt een zorginfectie genoemd. Een deel van de zorginfecties ontstaat na een operatie. In de periode 2007 tot en met 2012 is een steekproef gehouden onder een deel van de Nederlandse ziekenhuizen. Enkele resultaten hiervan zijn in de tabel te zien. |
||||||||||||
|
|||||||||||||
|
We nemen aan dat de patiënten in deze ziekenhuizen
representatief zijn voor alle patiënten die in een Nederlands ziekenhuis
worden opgenomen. Dan kunnen we op basis van de gegevens in de tabel schatten hoeveel procent van alle in Nederland geopereerde patiënten in de genoemde periode een zorginfectie opliep. Bereken het 95%-betrouwbaarheidsinterval van dit percentage. Rond de getallen in je eindantwoord af op één decimaal. |
|||||||||||||
|
|||||||||||||
| 7. |
Examenopgave Havo,
Wiskunde A, 2016. Op basis van deze gegevens worden de volgende twee uitspraken gedaan over het percentage Nederlanders dat (in 2013) vertrouwen had in de medemens: |
||||||||||||
| 1. |
Het is meer dan 95% zeker dat het percentage
Nederlanders dat vertrouwen had in de medemens, in het interval [56,6 ; 59,4] ligt. |
||||||||||||
| 2. |
Het is minder dan 95% zeker dat het percentage
Nederlanders dat vertrouwen had in de medemens, in het interval [56,6 ; 59,4] ligt. |
||||||||||||
|
Eén van deze twee uitspraken is juist. Welke uitspraak is juist? Licht je antwoord met een berekening toe. |
|||||||||||||
| 8. |
Examenopgave Havo,
Wiskunde A, 2021-III. In 2018 hebben 674 leerlingen van een scholengemeenschap een vragenlijst ingevuld. Zij vormden een aselecte en representatieve steekproef uit de gehele leerlingenpopulatie van de school. De school kreeg van deze leerlingen een gemiddelde score van 7,24 op het onderwerp ‘begeleiding’. Het 95%-betrouwbaarheidsinterval voor de gemiddelde score van alle leerlingen van de school op het onderwerp ‘begeleiding’ was [7,13; 7,35]. Bereken de standaardafwijking die bij deze steekproef hoort op dit onderwerp. Geef je antwoord in drie decimalen. |
||||||||||||
|
|||||||||||||
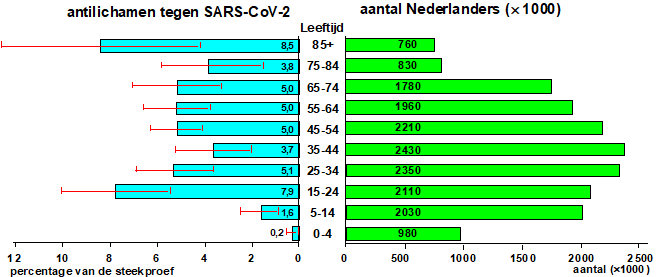
| 9. |
Een
persoon die corona heeft gehad heeft in zijn bloed antilichamen tegen
covid ontwikkeld. Om een aanwijzing te krijgen over het aantal
coronagevallen heeft de bloedbank Sanguin daarom in juni/juli van 2020
een onderzoek gedaan naar het aantal bloedmonsters dat antilichamen
tegen Covid bevat. |
||||||||||||
|
|
|||||||||||||
|
De blauwe staafjes links geven per leeftijdsgroep aan welk percentage van de bloedmonsters uit de steekproef antilichamen bevatte. De groene staafjes rechts geven van dezelfde leeftijdsgroepen de totale aantallen Nederlanders. In de staafjes staat steeds aangegeven welk aantal erbij hoort. |
|||||||||||||
| a. |
Stel dat de gemeten percentages in de steekproef precies gelden voor de hele populatie. Hoeveel procent van alle Nederlanders had in juni/juli dan antilichamen in zijn bloed? |
||||||||||||
|
|||||||||||||
| De rode lijntjes die bij de blauwe staafjes getekend zijn geven de 95%-betrouwbaarheidsintervallen van de gemeten percentages aan. | |||||||||||||
| b. |
Het 95%-betrouwbaarheidsinterval voor de groep 75-84 jaar is ongeveer [1.7 ; 5.9]. Bereken dit interval nauwkeuriger (geef de procenten in 2 decimalen) als je weet dat het gemiddelde precies 3,8% was, en dat er 334 mensen van die leeftijdsgroep in de steekproef zaten. |
||||||||||||
|
|||||||||||||
| c. |
De
staafjes voor de drie groepen 45-54 en 55-64 en 64-74 zijn precies
gelijk (namelijk 5,0%), maar de betrouwbaarheidsintervallen niet. |
||||||||||||
|
In deze twee maanden waren er in totaal 11530 ziekenhuisopnamen waarvan er 2915 op de IC terechtkwamen. 7828 mensen van deze ziekenhuisopnamen hadden obesitas (zwaar overgewicht) en daarvan kwamen er 2604 op de IC. |
|||||||||||||
| d. | Onderzoek of het verschil in aantal mensen dat op de IC terecht komt tussen de mensen met of zonder obesitas groot, middelmatig of gering is | ||||||||||||
| 10. |
Examenopgave Havo,
Wiskunde A, 2023-II. Sinds het begin van deze eeuw daalt het totaal aantal geregistreerde misdrijven, met name door een daling van het aantal geregistreerde vermogensmisdrijven. Een voorbeeld van een vermogensmisdrijf is een woninginbraak. Iemand vermoedt dat er in het begin van deze eeuw bij een kleiner percentage van de woningen werd ingebroken dan aan het eind van de vorige eeuw. Om hier zicht op te krijgen is in 2004 in een aselecte steekproef uit de woningen gekeken bij welk percentage er in dat jaar was ingebroken. De resultaten kunnen worden vergeleken met die van een aselecte steekproef uit de woningen in 1998. Zie de tabel. |
||||||||||||
|
|||||||||||||
| De tabel laat zien
dat het steekproefpercentage woningen waarbij is ingebroken in 2004
lager is dan in 1998. Onderzoek of het steekproefpercentage uit 2004 in het 95%-betrouwbaarheidsinterval ligt van het populatiepercentage in 1998. |
|||||||||||||
|
|
|||||||||||||
|
© h.hofstede (h.hofstede@hogeland.nl) |
|||||||||||||