|
|||||
| De positie van een schijf. | |||||
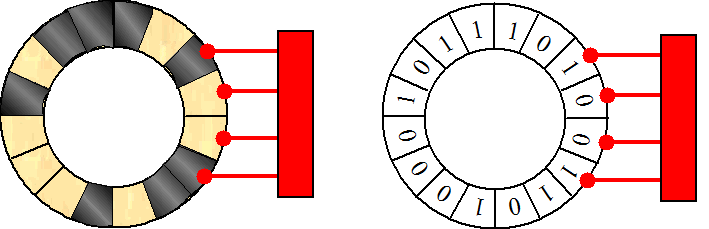
| Stel we hebben in één of ander meetsysteem een draaiende schijf waarvan het belangrijk is dat we de stand kunnen aflezen. De rand van de schijf is gecodeerd, er zijn een aantal vakjes (in dit voorbeeld 16) die met geleidend materiaal zijn bedekt of met isolatiemateriaal. Op 4 contactpunten wordt gemeten of het vakje van de schijf geleidend is of niet. Laten we geleidend `1` noemen en niet/geleidend `0`, zoals je rechtsonder ziet. We lezen in deze stand de code 1-0-0-1 (met de klok mee) af. | |||||
|
|
|||||
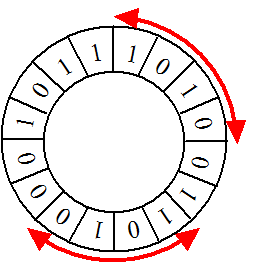
| Maar nou komt het probleem:
de positie van de hier getekende schijf is niet eenduidig bepaald als
bekend is wat de vier contacten opleveren. Kijk maar hiernaast:
beide rode posities bij de contacten geven de serie 1-0-1-0 dus daar
zien we geen verschil tussen. Ofwel: deze indeling van geleidende
en isolerende vlakjes is niet zo handig. Je snapt de vraag waarschijnlijk al wel: Is er een nummering te maken die alle verschillende posities eenduidig herkent? Laten we de vraag even nauwkeuriger formuleren: Stel dat we 2n standen van de schijf willen herkennen. Hoe kunnen we dat doen met zo min mogelijk contactpunten? |
|
||||
| Stel dat we c
contactpunten hebben, dan geven die een binair getal, waarvoor er 2c
mogelijkheden zijn. Maar de schijf heeft 2n standen, dus als al die standen een verschillend "contactgetal" moeten opleveren, dan moet gelden 2c ≥ 2n dus c ≥ n Het zal zo meteen blijken dat c = n lukt!! |
|||||
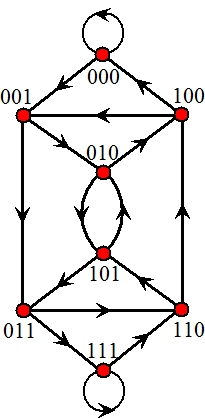
| We maken een digraaf D met als knooppunten de binaire getallen met n
- 1 cijfers. Verder maken we een verbindingslijn vanaf knoop K door van de cijfers van K het meest linkercijfer weg te laten, en aan de rechterkant een 1 of een 0 toe te voegen. De verbindingslijnen lopen dan van knoop K naar de twee knooppunten die bij de twee nieuwe getallen horen. Bijvoorbeeld: als n = 5 zijn er 25 = 32 posities. Graaf D bestaat dan uit de binaire getallen van 4 cijfers (dat zijn dus 16 knooppunten). Er loopt vanaf knooppunt 10111 een verbindingslijn naar 01110 en naar 01111. De voorste 1 gaat weg, en achteraan voegen we een 1 of een 0 toe. Voor n = 4
(16 posities op de schijf, 8 knooppunten in D) geeft dat de graaf hiernaast. |
|
||||
 |
|||||
| In de figuur ernaast is een blauwe Eulerroute in de graaf getekend
(begonnen bij 111), en de groene getallenkolom daar weer naast geeft de namen
van de achtereenvolgende verbindingslijnen op die route (van boven naar
beneden). Als je nou de eerste cijfers van die namen van die
verbindingslijnen achter elkaar zet, dan krijg je een goede nummering
voor de schijf! In dit geval 1111000011010010. Helemaal rechts staat het eindresultaat. Deze coole toepassing van gerichte Eulerroutes komt overigens van Good (1946). |
|||||
| De Bruijn Rijen. | |||||
| De rij op de schijf die we hierboven vonden is een voorbeeld van een "De-Bruijn-Rij" (genoemd naar de Nederlandse wiskundige Nicolaas Govert de Bruijn). De algemene definitie is: | |||||
|
|||||
| Hierboven vonden we dus de rij
B(2, 4) want we hadden twee objecten (een 1 en een 0) en we
bekeken rijtjes van lengte 4. We noemen n ook wel de
orde van de rij. En rijen met
k = 2 heten heel toepasselijk wel
binaire rijen. Hierboven zagen we al hoe je zo'n rij uit een graaf kunt maken. |
|||||
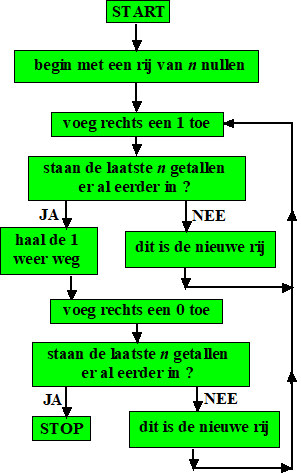
| Het kan ook met een simpel
algoritme: Het "prefer-one algoritme". Hoe dat werkt zie je hiernaast. Voor n = 3 zou dat de volgende serie geven: |
 |
||||
|
|||||
| Mooi toch? Ionica Smeets wijdde er toen de Bruijn in 2012 overleed in de Volkskrant zelfs een column aan.... https://www.volkskrant.nl/archief/wat-er-zo-bijzonder-is-aan-0000111101100101000~a3226643/ |
|||||
|
© h.hofstede (h.hofstede@hogeland.nl) |
|||||