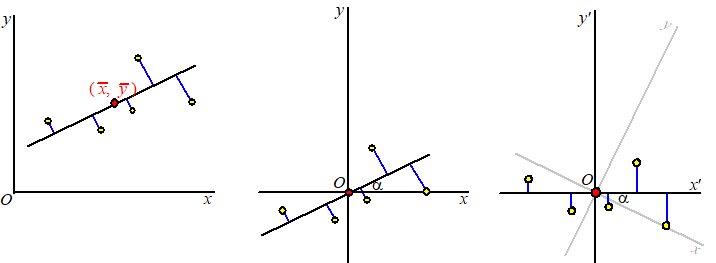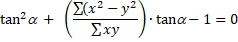© h.hofstede (h.hofstede@hogeland.nl)

Loodrechte regressie.
       
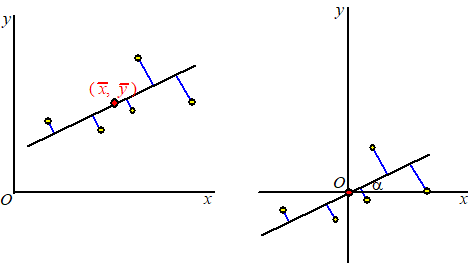
Bij lineaire regressie gingen we een regressielijn zó kiezen dat de som van de kwadraten van de verticale afstanden van onze punten tot die lijn minimaal werd. Dat was de methode van de kleinste kwadraten. En bij regressie van x op y minimaliseerden we de kwadraten van de horizontale afstanden, maar dat kwam in feite op hetzelfde neer, als we gewoon x en y verwisselen.

Het kan natuurlijk ook anders.....

Waarom zouden we niet proberen de loodrechte afstanden te nemen? Gewoon de kortste afstanden!
Dat zou er zó uitzien:
       

       
Laten we proberen de som van de kwadraten van die blauwe lijntjes te minimaliseren.

Eerste probleem.
Het eerste probleem daarbij is, dat de eenheden van x en y niet gelijk hoeven te zijn. Het zou bijvoorbeeld kunnen dat x een tijd voorstelt en y een lengte. Hoe kunnen we ons dan in vredesnaam wat zinvols voorstellen bij de lengte van zo'n blauw lijntje? En wat stelt  "loodrecht" dan voor?
Het is misschien het meest zinvol om te kijken naar de relatieve lengte van zo'n lijntje. Dan bedoel ik de relatieve lengte in de x-richting vergeleken met alle x-waarden, en de relatieve lengte in de y-richting vergeleken met alle y-waarden. Laten we daarom afspreken dat we de eenheden in de x- en y-richting zó kiezen dat de standaarddeviatie van de x-waarden gelijk is aan die van de y-waarden.

Een slimme aanpak.
Oké, stel dat we een geschikt geschaalde set van punten (xi , yi) hebben.
Noem het gemiddelde van de x-waarden x , en dat van de y-waarden  y . Dan is het centrale punt dus  (x , y).
Als je van alle x-en nu x  aftrekt, en van alle y-en  y, dan heb je een nieuwe puntenwolk met als centraal punt de oorsprong:
       

       
Vervolgens draaien we de hele puntenwolk over een hoek α, die de (nog onbekende) regressielijn met de x-as maakt, zodat al die blauwe lijnstukjes verticaal komen te liggen:
       

       
De punten van de wolk krijgen daardoor nieuwe coördinaten (X, Y)  waarvoor geldt:
       
X =  xcosα + ysinα
Y =  -xsinα + ycosα
       
Nu is het onze taak om α zodanig te kiezen dat de som van de kwadraten van die verticale blauwe lijntjes minimaal wordt.

Laten we die som S noemen.
Wanneer is iets minimaal?  Als de afgeleide ervan nul is natuurlijk!  In dit geval de afgeleide naar α .

De afgeleide van Y2  is  2 • Y • Y'   en  Y' =  dY/dα = -xcosα - ysinα,
Dat geeft dus:

De factor 2 doet er niet toe, want het moet immers nul worden.
Haakjes wegwerken:

groeperen en delen door  cos2α:

Alles delen door  Σxy :

Dat is een kwadratische vergelijking voor tanα.  Dat geeft twee oplossingen waarvan er eentje de som S zal minimaliseren en de ander de som S zal maximaliseren.
       
Testvoorbeeldje.
       
Neem de puntenwolk met de punten (1, 1) en (2, 2) en (3, 3) en (4, 4). Dat is de lijn y = x dus dat zal als het goed is een hoek α = 45º moeten opleveren.
Testen maar:
Σ(x2 - y2) = (12 - 12) + (22 - 22) + (32 - 32) + (42 - 42) = 0
Σ(xy) = 1 • 1 + 2 • 2 + 3 • 3 + 4 • 4 = 30
De vergelijking wordt  tan2α - 1 = 0   dus tanα = ±1 en dat geeft inderdaad α = ±45º
       
Echt voorbeeldje.
       
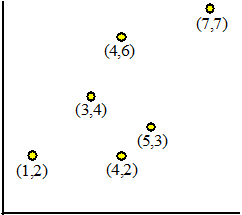
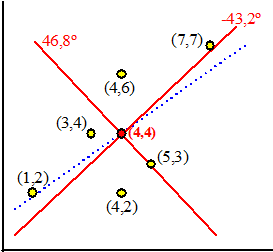
Neem de puntenwolk van de zes punten hiernaast.
Het centrale punt is  (4, 4), en als dat van alle punten aftrekt krijg je de punten (-3, -2) (-1, 0) (0, -2) (1,-1) (0, 2) en (3,3)

Σ(x2 - y2)
= (32 - 22) + (12 - 02) + (02 - 22) + (12 - 12) + (02 - 22) + (32 - 32)
= 5 + 1 - 4 + 0 - 4 + 0 = -2

Σ(xy) = 6 + 0 + 0 - 1 + 0 + 9 = 16

Dat geeft de vergelijking  tan2α - 2/16tanα - 1 = 0  met als oplossingen
tanα = -0,9395  en  tanα = 1,0645
Dat zijn de hoeken α = -43,2º  en  α = 46,8º 

Hieronder zijn beide lijnen rood getekend.  Die van -43,2º geeft de minimale S, en is de lijn  y = 0,94x + 0,24.
Ter vergelijking:  "gewone" lineaire regressie van x op y zou de regressielijn y = 0,7x + 1,2 geven, die is er blauw bij ingetekend (de hoek met de x-as daarvan is  35º).
       

       

© h.hofstede (h.hofstede@hogeland.nl)