© h.hofstede (h.hofstede@hogeland.nl)

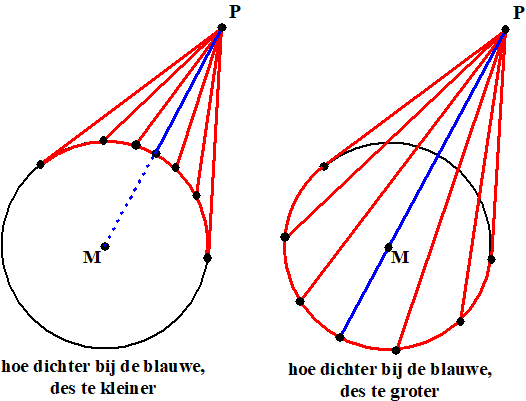
Boek III, propositie 8.
       

Teken vanuit een punt P buiten een cirkel lijnen naar punten op de omtrek van die cirkel.

Van de lijnen naar het concave deel is de lijn door PM de grootste, en hoe dichter bij die lijn,
des te groter worden de lijnen.

Van de lijnen naar het convexe deel is het deel van PM het kleinste, en hoe dichter bij die lijn, des te kleiner worden de lijnen.

Verder zijn er steeds twee even groot; aan elke kant van PM één.
       

       
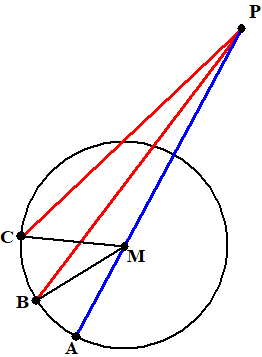
MB = MA  (straal cirkel)
tel bij beiden PM op:  MB + PM = PA

Maar MB + PM is groter dan PB  (driehoeksongelijkheid) (I-20)
Dus is PA groter dan PB (en op dezelfde manier ook groter dan PC, PD, ...) dus PA is de grootste

De driehoeken MBP en MCP hebben twee gelijke zijden (MB = MC en MP = MP) en dan heeft de driehoek met de grotere hoek daartussen ook de grotere basis (I-24)
Dus PB is groter dan PC.

Op dezelfde manier vind je dat lijnen dichter bij A groter zijn




 

       
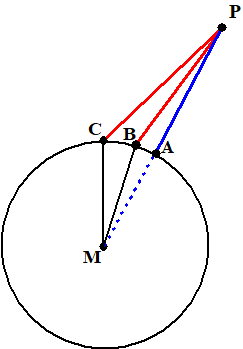
MC + CP is groter dan MP (driehoeksongelijkheid)   (I-20)

MC = MA  (straal cirkel), dus die kun je van beiden aftrekken.
Dan blijft over CP is groter dan  AP
En op dezelfde manier BP > AP dus AP is de kleinste. 

Binnen driehoek MCP zijn MB en BP twee elkaar ontmoetende lijnen. Dan is MB + BP  <  MC + CP   (I-21)
Trek van beiden MC = MB af,
Dat geeft  BP < CP.

Op dezelfde manier vind je dat lijnen verder van A af groter zijn.
 

       
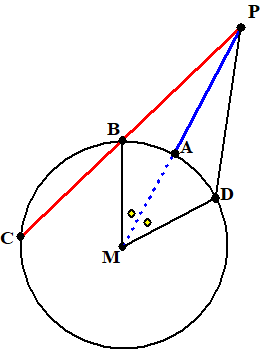
Neem een willekeurige lijn PB.
Construeer hoek PMD gelijk aan hoek PMB   (I-23)

MB = MD
MP = MP
Dus de driehoeken MBP en MDP zijn congruent (ZHZ)   (I-4)
Dus PB = PD

Er is niet nog een andere lijn even groot als PB:
Stel dat PE even groot als PD is
Dan is PB = PE en ook PB = PD  dus zijn PD en PE even groot. Maar dat kan niet want de lijn dichter bij PA is kleiner dan de lijn verder van PA af (zie hierboven)

       

© h.hofstede (h.hofstede@hogeland.nl)