| |
© h.hofstede (h.hofstede@hogeland.nl)
|
|
|
1. De ingeschreven cirkel van
een driehoek. |
| |
|
|
|
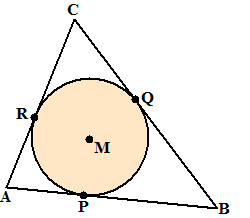
In elke driehoek kun
je een cirkel tekenen die "er precies in past". Dat wil zeggen dat
elke grotere cirkel niet in de driehoek past. Die cirkel raakt dus alle
zijden van de driehoek (als er nog ruimte was kon je hem een klein
stukje opschuiven en groter maken). 't Is of je een ballon in de
driehoek legt en hem dan langzaam opblaast totdat hij precies "klemzit".
Dat betekent dat de zijden van de driehoek de raaklijnen aan de cirkel
zijn.
Maar dat betekent (zie de figuur) dat het punt M gelijke afstanden tot
de raakpunten P, Q en R heeft (namelijk de straal van de cirkel)
MP staat loodrecht op BC (eigenschap van de raaklijn aan een
cirkel) dus is MP ook de kortste afstand van M naar PC. En zo zijn
ook MQ en MR de afstanden van M tot BC en AC. Kortom: M
heeft gelijke afstanden tot alle zijden van de driehoek. |
 |
| |
|
|
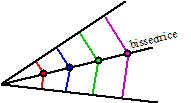 |
Maar hoe heetten alle punten die gelijke afstanden tot twee lijnen
hadden ook alweer? Precies! Dat was de bissectrice!!
Conclusie: |
| |
|
|
|
|
Het middelpunt van de
ingeschreven cirkel van een
driehoek
is het snijpunt van de bissectrices van de zijden. |
|
| |
|
|
|
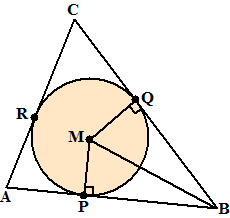
Een netter bewijsje
zie je hiernaast.
MQ = MP (straal van de cirkel)
MB = MB (nogal logisch)
∠MQB = ∠MPB = 90º (raaklijneigenschap van cirkel)
Daaruit volgt
ΔPMB ≅
ΔQMB (ZZR)
Dus is ∠PBM = ∠QBM
Dus is BM bissectrice van ∠PBQ |
 |
| |
|
|
|
|
2. De omgeschreven cirkel van
een driehoek. |
| |
|
|
|
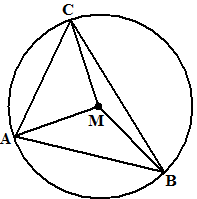
In elke driehoek kun
je een cirkel tekenen die "er precies omheen past". Dat wil zeggen
dat alle drie de hoekpunten precies op de cirkel liggen. 't Is of je een
ballon om de driehoek legt en hem dan langzaam leeg laat lopen totdat de
driehoek precies "klemzit".
Dat middelpunt M heeft dus gelijke afstanden tot de drie hoek[punten van
de cirkel (namelijk de straat van de cirkel). Dus
bijvoorbeeld MA = MB
Daar gaan we weer:
Hoe heetten alle punten die gelijke afstanden tot twee punten A en B
hadden ook alweer? Precies! Dat was de middelloodlijn van AB.
Conclusie: |
 |
| |
|
|
|
|
Het middelpunt van de
omgeschreven cirkel van een driehoek
is het snijpunt van de middelloodlijnen van de hoekpunten |
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
|
OPGAVEN |
| |
|
|
|
| 1. |
Examenopgave VWO wiskunde B,
2016-I |
| |
|
|
|
| |
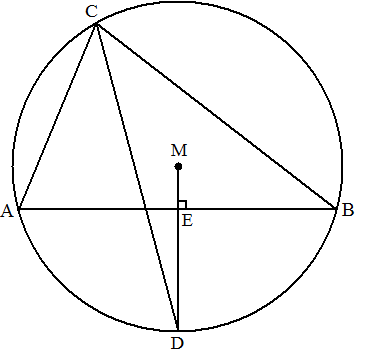
Punt M is het middelpunt van de omgeschreven
cirkel van de scherphoekige driehoek ABC.
Op deze cirkel ligt punt D zo dat straal MD zijde AB
in punt E loodrecht snijdt.
Zie de figuur hiernaast.
Bewijs dat CD de bissectrice van hoek ACB
is. |
 |
| |
|
|
|
| 2. |
Examenopgave VWO wiskunde B,
2016-I |
| |
|
|
|
| |
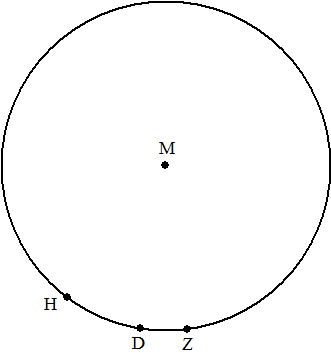
I n de figuur
hiernaast is de omgeschreven cirkel getekend van een andere driehoek
ABC. Op deze cirkel met middelpunt M liggen de punten H, D
en Z.
Voor driehoek ABC geldt: |
 |
| |
|
|
| |
- |
D ligt
zodanig op de cirkel dat MD loodrecht staat op AB |
| |
- |
H is het
snijpunt van het verlengde van de hoogtelijn vanuit C met de
cirkel; |
| |
- |
Z
is het snijpunt van de lijn door C en het snijpunt E
van MD en AB met de cirkel. |
| |
|
|
| |
Teken driehoek ABC in de figuur hiernaast. Licht je
werkwijze toe. |
| |
|
|
|
| |
|
|
 |
|
| |
|
|
|
|
© h.hofstede (h.hofstede@hogeland.nl)
|