| |
|
©
h.hofstede (h.hofstede@hogeland.nl) |
| |
|
|
| 1. |
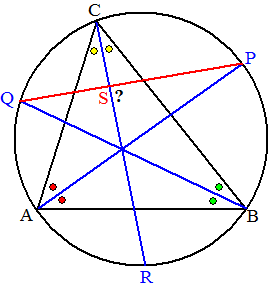
De bissectrices van een driehoek
ABC snijden de omgeschreven cirkel in P, Q en R.
Toon aan dat PQ loodrecht op CR staat. |
 |
| |
|
|
| 2. |
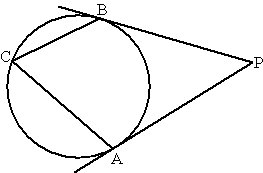
Vanuit punt P zijn twee raaklijnen
aan een cirkel getekend, die de cirkel raken in A en B. Vanuit een
willekeurig punt C worden de lijnen CA en CB getrokken.
Bereken hoek ACB
als gegeven is dat hoek BPA gelijk is aan 50º. |
 |
| |
|
|
|
| |
|
|
|
| 3. |
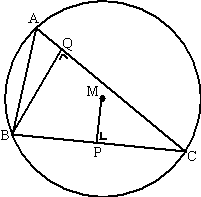
Van driehoek ABC liggen de
hoekpunten op een cirkel waarvan de straal gelijk is aan AB.
BQ is een hoogtelijn van deze driehoek.
MP staat loodrecht op BC.
Bewijs dat AQ = MP. |
 |
| |
|
|
|
| 4. |
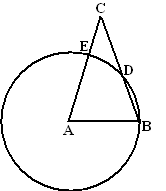
In de figuur hiernaast
is een scherphoekige driehoek ABC getekend met AC > AB, en ook
de cirkel met middelpunt A en straal AB.
De cirkel snijdt BC in D en AC in E.
Toon aan dat ∠CDE = 1/2
• ∠BAC |
 |
| |
|
|
|
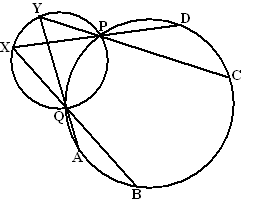
| 5. |
Twee cirkels snijden
elkaar in P en Q.
X en Y zijn twee willekeurige punten op de ene cirkel.
XP, XQ, YP en YQ snijden de andere cirkel
in D, B, C en A.
Bewijs dat boog AC = boog BD. |
 |
| |
|
|
|
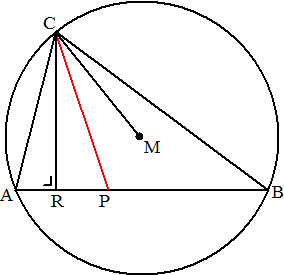
| 6. |
CP is bissectrice van
hoek C in driehoek ABC (Dus ∠ACP = ∠BCP
CR is een hoogtelijn van die driehoek.
M is het middelpunt van de omgeschreven cirkel van die driehoek.
Toon aan dat ∠RCP = ∠PCM
|
 |
| |
|
|
|
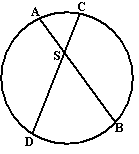
| 7. |
AB en CD zijn koorden
van een cirkel, die elkaar snijden in punt S.
Toon aan dat geldt AS • SB = CS • SD |
 |
| |
|
|
| |
| hint: |
toon aan dat ASD en BSC gelijkvormig zijn |
|
| |
|
|
|
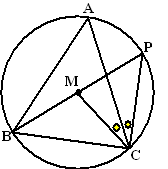
| 8. |
Van driehoek ABC liggen
de hoekpunten op een cirkel met middelpunt M. Het verlengde van
BM snijdt de cirkel in punt P.
Het blijkt dat AC voor deze keuze van ABC toevallig de bissectrice
van ∠PCM is.
Toon aan dat daaruit volgt dat AB = AC. |
 |
| |
|
|
|
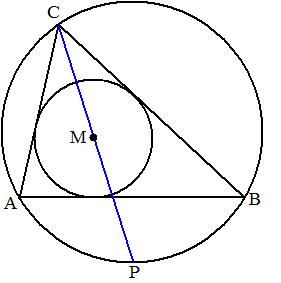
| 9. |
Hiernaast zie je een
driehoek ABC met zijn ingeschreven en omgeschreven cirkel.
M is het middelpunt van de ingeschreven cirkel.
P is het midden van koorde AB
a. Toon aan dat M op PC ligt
b. Toon aan dat PB = PM |
 |
| |
|
|
|
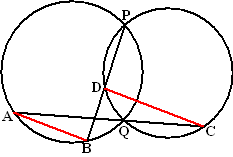
| 10. |
Twee cirkels snijden
elkaar in de punten P en Q.
AB is een willekeurige koorde op de eerste cirkel.
AQ snijdt de tweede cirkel ook nog in punt C
BP snijdt de tweede cirkel ook nog in punt D.
Toon aan dat AB en CD evenwijdig zijn. |
 |
| |
|
|
|
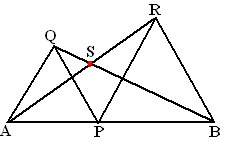
| 11. |
Op lijnstuk AB wordt
een willekeurig punt P getekend. De driehoeken AQP en PRB zijn
gelijkzijdig.
S is het snijpunt van BQ en AR.
Toon aan dat alle punten S op een cirkel liggen. |
 |
| |
| |
|
| hint: |
Toon aan dat APR en PQB congruent zijn |
|
| |
|
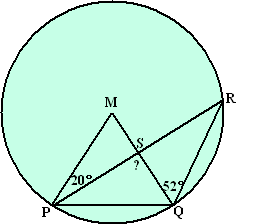
| 12. |
Bereken
de hoek met het vraagteken.
M is het middelpunt van de cirkel. |
 |
| |
|
|
|
| |
|
|
|
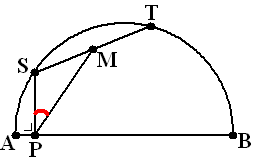
| 13. |
De eindpunten van
lijnstuk ST bewegen langs een halve cirkelboog met diameter AB.
M is het midden van ST, en P ligt op AB zodat SP loodrecht op AB staat.
Bewijs dat hoek SPM constant is. |
 |
| |
|
|
| |
|
| |
|
|
|
| 14. |
Gegeven is een
cirkel met koorde AB. Het punt P ligt op de cirkel.
Punt X ligt op het
verlengde van BP zodanig dat AP
= XP
Als P de dikke boog AB doorloopt, beschrijft X een baan in het vlak.
Bewijs dat de baan van X een deel van een cirkel is. |
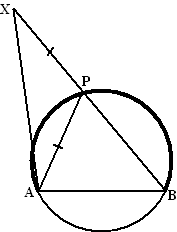 |
| |
|
|
|
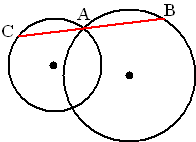
| 15. |
Gegeven
zijn twee snijdende cirkels.
Kies een snijpunt A en teken een rechte lijn door A die de cirkels
verder in B en C snijdt We gaan in deze opgave op jacht naar het langst
mogelijk lijnstuk BC. |
 |
| |
|
|
| |
a. |
Noem het andere snijpunt van
de twee cirkels punt D.
Bewijs dat alle driehoeken BCD gelijkvormig zijn. |
| |
|
|
|
| |
b. |
Als alle driehoeken BCD
gelijkvormig zijn bestaat er tussen BC en BD een vaste verhouding.
Construeer met dit in gedachten het langste lijnstuk BC. |
| |
|
|
|
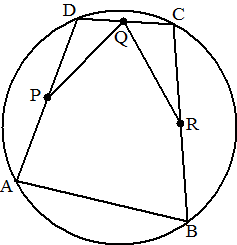
| 16. |
Op een cirkel liggen de
punten A. B, C en D
P, Q en R zijn de middens van AD, DC en BC
Toon aan dat ∠DPQ = ∠CRQ |
 |
| |
|
|
|
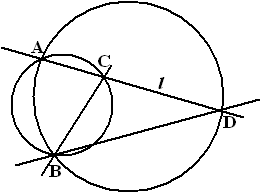
| 17. |
Examenvraagstuk VWO Wiskunde B,
2003 Gegeven zijn twee cirkels die elkaar snijden
in de punten A en B.
Lijn l gaat door het punt A en snijdt de cirkels in de
punten C en D. Zie de figuur hiernaast.
Door de lijn l om A te draaien
verandert driehoek BCD. |
 |
| |
|
|
| |
a. |
Toon aan dat de grootte van ∠CBD
onafhankelijk is van de stand van l. |
| |
|
|
|
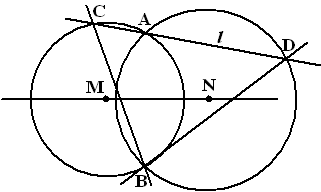
| |
In de figuur hiernaast zijn opnieuw twee
cirkels getekend die elkaar snijden in de punten A en B. De middelpunten
van de cirkels zijn M en N. Lijn l door het punt A snijdt de
cirkels weer inde punten C en D. |
 |
| |
|
|
| |
b. |
Bewijs dat ∠AMN = ∠ACB |
| |
|
|
| |
c. |
Bewijs dat ∠MAN = ∠CBD |
| |
|
|
|
| 18. |
Examenvraagstuk VWO Wiskunde B,
2007 |
| |
|
|
 |
| |
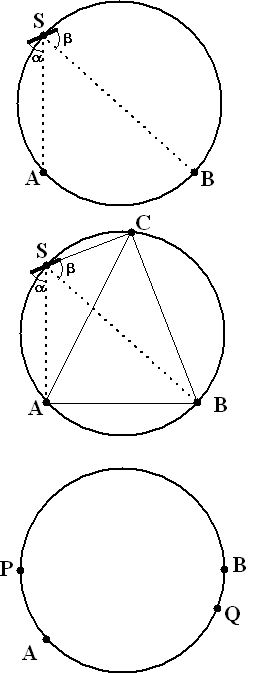
De punten A en B liggen op een
cirkel.
In het punt S op de cirkel plaatsen we een vlak spiegeltje zo dat de
lichtstraal vanuit A wordt weerspiegeld naar B. De hoek
α
die AS met de spiegel maakt is dus gelijk aan de hoek
β
die SB met de spiegel maakt. Zie de bovenste figuur hiernaast.
Als we de lijn van de spiegel in S verlengen snijdt deze de cirkel
in punt C. Zie de middelste figuur hiernaast.
Er geldt: ∠BAC = ∠ABC |
| |
|
|
| |
a. |
Toon dit aan. |
| |
|
|
| |
De omgekeerde bewering is
ook waar:
als in driehoek ABC geldt ∠BAC = ∠ABC,
dan geldt voor elk punt S op de omgeschreven cirkel van driehoek ABC
α
=
β, waarbij
α en
β de hoeken zijn die respectievelijk AS en BS met lijn
CS maken.
In de onderste figuur hiernaast zijn twee andere punten A en B op de
cirkel getekend en verder nog twee punten P en Q op de cirkel.
In P en Q willen we een spiegeltje zo plaatsen dat in elk van beide
spiegeltjes lichtstralen van A weerkaatst worden naar B. |
| |
|
|
| |
b. |
Hoe kun je de omgekeerde bewering gebruiken
om de juiste stand van de spiegeltjes bij P en Q te tekenen? Licht je
antwoord toe met een tekening. |
| |
|
|
|
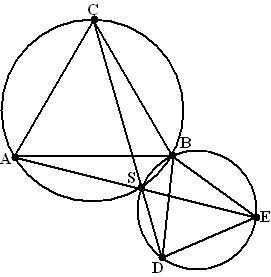
| 19. |
Examenvraagstuk VWO
Wiskunde B, 2008.
In de figuur hiernaast zijn van de twee gelijkzijdige driehoeken ABC
en BDE
ook de omgeschreven
cirkels getekend. Deze omgeschreven cirkels hebben de punten B
en S
gemeenschappelijk. Ook zijn de
lijnstukken AS en
SE getekend.
Bewijs dat
hoek ASE een
gestrekte hoek is. |
 |
| |
|
|
|
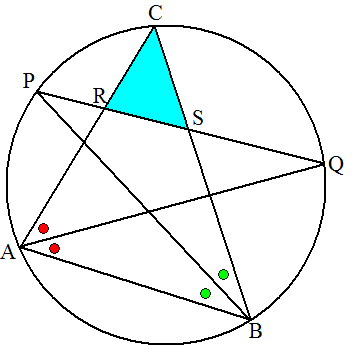
| 20. |
Van driehoek ABC
snijden de bissectrices van hoek A en van hoek B de omgeschreven
cirkel in de punten Q en P.
QP snijdt AC in R en BC in S
Toon aan dat driehoek CRS gelijkbenig is.
|
 |
| |
|
|
|
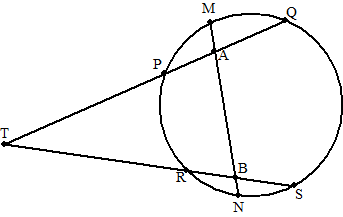
| 21. |
PQ en RS zijn twee
bogen van een cirkel.
De lijnen PQ en RS snijden elkaar in T
M is het midden van boog PQ, N is het midden van boog RS
MN snijdt TQ in punt A en TS in punt B
Toon aan dat TA = TB |
 |
| |
|
|
| 22. |
Examenvraagstuk VWO
Wiskunde B, 2013. |
|
| |
|
|
|
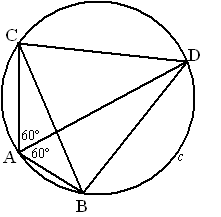
| |
Gegeven is driehoek ABC met ∠BAC
=120º
. De cirkel c is de omgeschreven
cirkel van driehoek ABC. De bissectrice van hoek A
snijdt de cirkel c in punt D. Zie de figuur.
Er geldt: driehoek BCD is
gelijkzijdig. |
 |
| |
|
|
| |
a. |
Bewijs dit. |
| |
|
|
| |
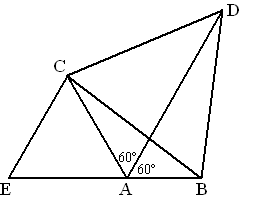
In de situatie van de figuur hierboven geldt: AD
=
AB + AC. Om dit te
bewijzen verlengen we BA en leggen we E op dit
verlengde zo dat EA =
AC . Er ontstaat een
gelijkzijdige driehoek ACE. In de figuur hieronder is deze
driehoek getekend.
|
| |
Het bewijs gaat verder met de volgende stappen:
-
Maak gebruik van de in vraag a) bewezen gelijkzijdigheid van driehoek BCD.
-
Toon aan dat de driehoeken CEB
en CAD congruent zijn. |
 |
| |
|
|
| |
b. |
Bewijs dat
AD =
AB + AC,
gebruikmakend van bovenstaande stappen. |
| |
|
|
|
| 23. |
ABC is een gelijkbenige
driehoek met tophoek C.
P is een willekeurig punt op AB.
Toon aan dat de cirkels door A, C, P en door B, C, P even groot
zijn. |
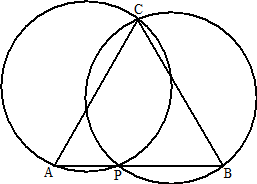 |
| |
|
|
|
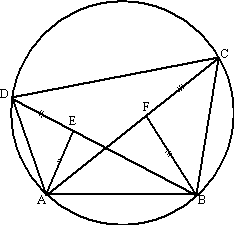
| 24. |
Examenvraagstuk VWO
Wiskunde B, 2013.
Gegeven is een vierhoek ABCD waarvan de hoekpunten op een
cirkel liggen, met
diagonalen AC en BD.
Op diagonaal BD ligt het punt E zo dat EA =
ED. Op diagonaal AC
ligt het punt F zo dat FC =
FB .
Zie de figuur.
De punten A, B, F
en E liggen op een cirkel. |
 |
| |
|
|
| |
a. |
Bewijs dit. |
| |
|
|
|
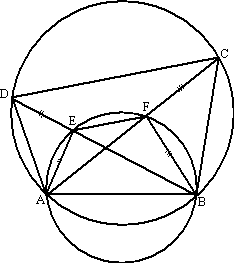
| |
In de figuur hiernaast zijn ook het
lijnstuk EF en de cirkel door A, B, F en
E getekend. |
 |
| |
|
|
| |
b. |
Bewijs dat EF evenwijdig is aan
DC. |
| |
|
|
|
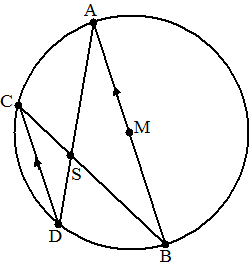
| 25. |
AB is een middellijn
van een cirkel met middelpunt M.
CD is een willekeurige koorde op deze cirkel, die evenwijdig is
aan AB.
BC en AD snijden elkaar in S.
Toon aan dat de punten C, S, M en A op een cirkel liggen. |
 |
| |
|
|
|
| 26. |
examenvraagstuk VWO
wiskunde B, 2015.
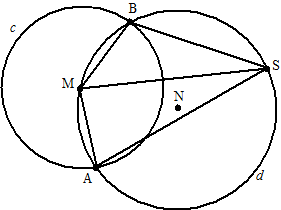
Gegeven is
cirkel c met middelpunt M. Op deze cirkel liggen de punten A
en B zo, dat door A, B en M een cirkel d met middelpunt N
gaat, waarbij N buiten c ligt.
Punt S ligt op cirkel d op de boog buiten cirkel c.
Zie de figuur.
Er geldt:
∠ASM = ∠BSM |
 |
| |
|
|
| |
a. |
Bewijs dit. |
| |
|
|
|
| |
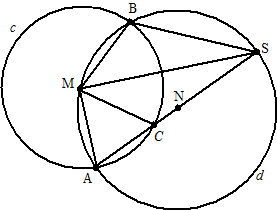
De hierboven
beschreven situatie geldt ook in de figuur hiernaast. Punt S is nu
zo gekozen dat lijnstuk AS door N gaat. Het snijpunt van AS en
cirkel c is het punt C. |
 |
| |
|
|
| |
b. |
Bewijs dat
∠AMC = ∠ASB |
| |
|
|
|
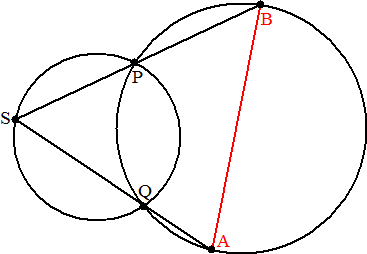
| 27. |
Twee cirkels snijden
elkaar in de punten P en Q.
S is een willekeurig punt van de eerste cirkel.
De verlengden van SQ en SP snijden de tweede cirkel in A en B
Toon aan dat AB constante lengte heeft, onafhankelijk van de
plaats van S |
 |
| |
|
|
|
| 28. |
M is het middelpunt van
een cirkel met straal 8.
Bereken AC in de figuur hiernaast. |
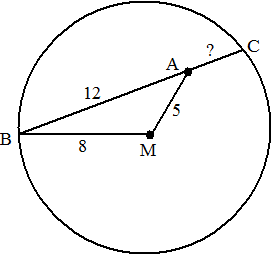 |
| |
|
|
|
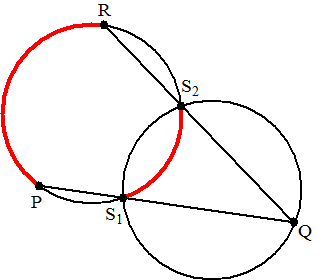
| 29. |
Twee even grote cirkels
snijden elkaar in S1 en S2.
P is een willekeurig punt van een van de cirkels.
De lijn PS1 snijdt de andere cirkel in Q
QS2 snijdt de eerste cirkel in R.
Zie de figuur.
Er geldt: boogPR = 2 • boog S1S2
Toon dat aan. |
 |
| |
|
|
|
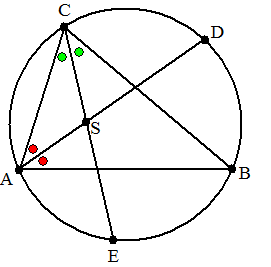
| 30. |
De bissectrices vanuit
de hoeken A en C van een driehoek worden verlengd tot zij de
omgeschreven cirkel snijden in D en E
S is het snijpunt van deze bissectrices.
Zie de figuur.
Toon aan dat de driehoeken CDS en AES gelijkbenig zijn. |
 |
| |
|
|
|
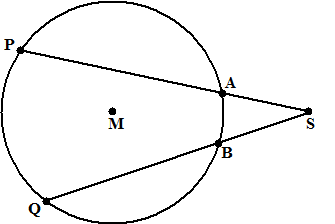
| 31. |
A, B, P en Q zijn
punten op een cirkel.
De lijnen PA en QB snijden elkaar in punt P buiten de cirkel,
waarbij het middelpunt M tussen de lijnen in ligt.
Toon aan dat 2 • ∠QSP = ∠QMP - ∠AMB |
 |
| |
|
|
| |
TIP: |
verleng AM en BM |
| |
|
|
|
| |
|
|
 |
|
©
h.hofstede (h.hofstede@hogeland.nl) |
| |
|
|
|