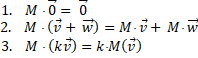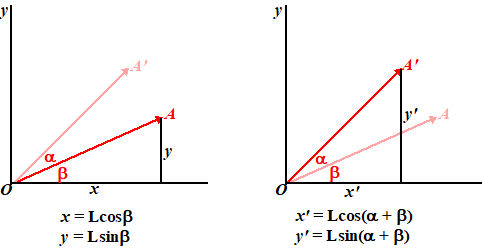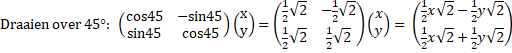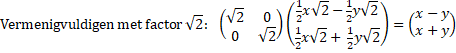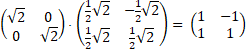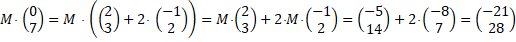lineaire transformaties

© h.hofstede (h.hofstede@hogeland.nl)

Lineaire Afbeeldingen.

Als je een punt uit het vlak als een vector opschrijft dan kun je die vector vermenigvuldigen met een 2×2 matrix M om een nieuwe (beeld)vector te krijgen.
Deze les zullen we bekijken hoe de getallen uit de matrix M bepalen wat het beeld van een vector wordt.
Nou ja... een beetje...

We beperken ons tot zogenaamde lineaire afbeeldingen en dat zijn afbeeldingen waarvoor geldt:

Laten we met een eenvoudig voorbeeldje beginnen.

Laten we maar gewoon wat punten proberen:

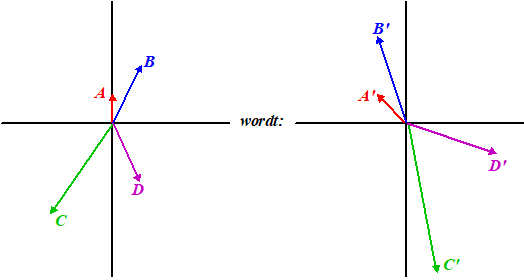
Dat geeft het volgende plaatje:

Zie je wat die matrix M "doet" met een vector?
Hij draait hem "een stukje" tegen de klok in, en maakt hem "ietsje" langer.
Preciezer onderzoek zal uitwijzen dat matrix M een vector draait over 45° en de lengte ervan vermenigvuldigt met √2
Dat heet een draaivermenigvuldiging.
Maar wat er in het vlak gebeurt is niet altijd zo mooi regelmatig. Als de vier getallen van de matrix willekeurig zijn, kun je meestal niet zo'n mooie beschrijving geven.

Laten we een paar speciale gevallen bekijken, dan komen we straks terug op die draaivermenigvuldigingen.

1. Vermenigvuldigingen (F).

Een vermenigvuldiging t.o.v. de oorsprong met een bepaalde factor k betekent dat je een vector alleen langer maakt, maar dat hij dezelfde richting houdt. Als je met een negatief getal vermenigvuldigt, dan wordt de richting tegengesteld.
Het natuurlijk duidelijk dat je dat voor elkaar kunt krijgen door gewoon elk kental met die factor te vermenigvuldigen.
We noteren dat als F_O,k en deze matrix hoort daarbij:

2. Spiegelingen (S).

• Als je een vector OA in de x-as spiegelt, dan draait het y-kental om.
• Als je een vector OA in de y-as spiegelt, dan draait het x-kental om.
• Als je een vector in de oorsprong spiegelt, dan draaien beide kentallen om.
Ik hoop dat je ziet dat dat precies is wat deze drie matrices doen.

Spiegelen in de oorsprong is natuurlijk precies hetzelfde als vermenigvuldigen met factor -1 t.o.v. de oorsprong.
Oh ja, een leuke is natuurlijk ook nog spiegelen in de lijn y = x: dan verwisselen de beide kentallen:

Spiegelingen in andere lijnen, daarover meer in de volgende les.

3. Rotaties (R).

Laten we proberen om een vector met lengte L en hoek β met de x-as om een hoek α te draaien:

Combineer de eerste met de tweede figuur, en gebruik de som- en verschilformules voor sinus en cosinus:
x ' = Lcos(α + β) = L(cosα • cosβ - sinα • sinβ) = xcosα - ysinα
y' = Lsin(α + β) = L(sinα • cosβ + cosα • sinβ) = xsinα + ycosα
Daarmee hebben we de matrix voor een draaiing over een hoek α (R_α) gevonden. Denk erom dat tegen de klok in positief is!

Draaivermenigvuldigingen.

Dat draaivermenigvuldigen is ineens een makkie!
Je draait eerst en vermenigvuldigt daarna (of andersom, dat maakt niet uit).
Neem het voorbeeld van helemaal bovenaan deze les: draaien over 45° en vermenigvuldigen met √2:

En dat laatste is inderdaad precies wat je krijgt als je op de vector de matrix helemaal bovenaan deze les toepast.
Je kunt die matrix gewoon krijgen door beide afzonderlijke matrices met elkaar te vermenigvuldigen. De volgorde waarin maakt niet uit.

De beelden van de basisvectoren.

Soms kun je heel snel de matrix van een lineaire afbeelding opstellen als je weet waarop de basisvectoren worden afgebeeld.
Immers er geldt:

Wat zien we?

"de kolommen van de matrix zijn de beelden van de basisvectoren"

Als je dus had gezien dat bij draaien over 45° en vermenigvuldigen met √2 precies geldt dat:

Dan had je direct in één keer die matrix op kunnen schrijven.

In het algemeen kun je ook die matrix opstellen als de beelden van twee willekeurige onafhankelijke vectoren bekend zijn (onafhankelijk betekent dat de enen niet een aantal keer de andere is)
Dat doe je gewoon door een stelsel vergelijkingen op te stellen.

Voorbeeld.

Voor een lineaire afbeelding geldt:

Geef de matrix die bij deze afbeelding hoort.

Oplossing 1.

De eerste geeft 2a + 3b = -5 ...(1) en 2c + 3d = 14 ...(2)
De tweede geeft -a + 2b = -8   ...(3)   en   -c + 2d = 7    ...(4)
uit (3) volgt a = 2b + 8 en dat kun je invullen in (1):   4b + 16 + 3b = -5 dus b = -3 en dan is a = 2
uit (4) volgt c = 2d - 7 en dat kun je invullen in (2):   4d - 14 + 3d = 14 dus d = 4 en dan is c = 1

Oplossing 2. Probeer nullen te maken om de beelden van de basisvectoren te vinden.

(Merk alsjeblieft even op dat de eigenschappen van helemaal bovenaan deze les van een lineaire afbeelding zijn gebruikt. Gedaan? Mooi, bedankt).

Op dezelfde manier kun je de eerste kolom van M vinden.


OPGAVEN