| |
© h.hofstede (h.hofstede@hogeland.nl)
|
|
|
Met of zonder ? |
 |
|
 |
Tja, daar denkt
natuurlijk iedereen aan bij "met of zonder".......
Wiskundig gaat het niet over mayonaise.
Waarover dan wel?
Daarvoor moeten we eerst twee speciale boomdiagrammen bekijken. |
| |
|
|
|
| TWEE
SPECIALE BOOMDIAGRAMMEN |
| |
|
|
|
| Er zijn twee soorten
boomdiagrammen die erg regelmatig zijn en bovendien in erg veel
telproblemen voorkomen. |
| |
|
|
|
|
1. De Machtsboom. |
| |
|
|
|
| De machtsboom is het meest regelmatige boomdiagram dat je je maar kunt
voorstellen, en zoals we zullen zien is het aantal takken daarvan dan
ook zeer makkelijk te tellen. De machtsboom herkennen we door: |
| |
|
|
|
| Het
aantal splitsingen is steeds gelijk |
|
| |
|
|
|
voorbeeld:
Je moet een multiple-choice proefwerk maken van 10 vragen met elke keer
de keuzes a, b, c of d. Als je elke keer moet gokken, hoeveel
mogelijkheden zijn er dan om deze vragen te beantwoorden?
Voor de eerste vraag zijn er 4 mogelijkheden. Maar voor de tweede
wéér 4, en voor de derde en elke volgende vraag wéér 4
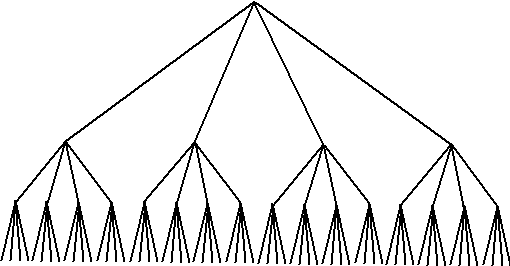
mogelijkheden. Een begin van het boomdiagram ziet er zó uit: |
| |
|
|
|
|
|
| |
|
|
|
Dit is uiteraard nog maar een
beginnetje: er zijn nog maar drie splitsingen (dus de antwoorden op 3
vragen) getekend. Het hele diagram zou 10 splitsingen geven. Dat valt
dus niet meer te tekenen.
Maar toch kunnen we uitrekenen hoeveel takken dat enorme diagram zou
krijgen. Immers er zijn elke keer 4 mogelijke keuzes, dus het aantal
takken wordt elke keer met 4 vermenigvuldigd.
Dat geeft na 10 splitsingen 4 • 4 • 4 • 4 • 4 • 4 • 4
• 4 • 4 • 4 = 1048576 takken.
Je kunt dit aantal natuurlijk snel uitrekenen: het is 410
. Vanwege dat tot-de-macht-nemen heeft zo'n volledig regelmatige boom de
naam machtsboom heeft gekregen.
Laten we nog heel even stilstaan bij de reden dat het getal 4 elke keer
weer voorkomt.
Dat komt natuurlijk omdat alle vier de mogelijkheden bij elke vraag er
weer zijn. Het is bijvoorbeeld niet zo dat een antwoord dat je al hebt
gekozen daarna niet meer voor kan komen.
Daarom noemen we dit soort telproblemen in de wiskunde wel problemen
met terugleggen
Het antwoord dat je op een vraag hebt gekozen wordt als het ware
teruggelegd zodat het bij de volgende vraag wéér gekozen kan worden.
2.
De Faculteitsboom.
Een faculteitsboom
kenmerkt zich door het feit dat het aantal splitsingen steeds eentje
minder wordt. Dat gebeurt steeds bij problemen waarbij er iets gekozen
moet worden, dat niet wordt teruggelegd, zodat bij de volgende keuze het
aantal mogelijkheden één minder is geworden.
We noemen dat daarom probleem zonder
terugleggen.Een faculteitsboom herken
je dus door: |
| |
|
|
|
| Het
aantal splitsingen wordt steeds één minder |
|
| |
|
|
|
| voorbeeld:
Ik heb een landkaart voor mij liggen met 4 landen. Die wil ik graag
gaan kleuren, en ik heb ook 4 verschillende kleurpotloden. Op hoeveel
manieren kan ik deze kaart inkleuren als elk land een verschillende
kleur moet krijgen?
Voor het eerste land kan ik kiezen uit 4 kleuren. Daarna voor het
tweede land nog uit drie kleuren (de eerste kleur is afgevallen want die
is al gebruikt) daarna voor het volgende land nog twee kleuren, en
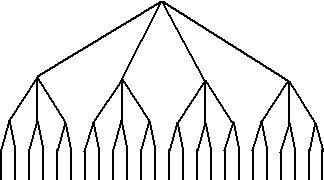
tenslotte voor het laatste land nog uit één kleur. Het boomdiagram ziet
er zó uit: |
|
|
Zoals je ziet telkens één
splitsing minder.
Het totaal aantal takken is 4 × 3 × 2 × 1 = 24. |
|
| |
|
|
|
| 4 × 3 × 2 × 1 kun je ook schrijven als 4 met een uitroepteken
erachter: 4! en ze spreken het uit als "4 faculteit"
(vandaar de naam faculteitsboom) |
Er is natuurlijk een knop voor op je GR.
Toets in 4 en dan
MATH -
PRB -
4: !
En je krijgt in één keer het antwoord 24. |
 |
| |
|
|
|
Faculteitsbomen die niet helemaal
tot 1 doorgaan.
Dat kan natuurlijk ook heel goed.
Als je een landkaart met 8 landen hebt, en je hebt 12 kleurpotloden,
dan wordt het aantal mogelijkheden:
12 • 11 • 10 • 9 • 8 • 7 • 6 • 5
want nu zijn er 8 landen gekleurd, dus zijn we al klaar.
En jawel! Ook hiervoor heeft je GR weer een knop.
Toets in 12 en dan MATH - PRB - nPr en dan 8 en
je krijgt in één keer het antwoord
(dus eerst het totaal aantal mogelijke keuzes (12) en daarna hoeveel je
er werkelijk moet kiezen (8))
Aantallen die je berekent ZONDER terugleggen heten ook wel
permutaties. |
| |
|
|
|
| |
|
|
|
OPGAVEN. |
| |
|
|
|
| 1. |
Gooi 50 keer met een
muntstuk en noteer elke keer of er KOP of MUNT uitkomt.
Hoeveel mogelijke series antwoorden zijn er? |
| |
|
|
|
| 2. |
Een kandidaat in een
televisiequiz heeft van de quizmaster 6 verschillende
prijskaartjes gekregen en moet die leggen bij 6 verschillende
artikelen. Op hoeveel manieren kan hij dat doen? |
| |
|
|
|
| 3. |
Er worden in de
eredivisie voetbal in een speelronde 13 wedstrijden gespeeld.
Als je met een totoformulier meespeelt om de uitslagen te
voorspellen, dan moet je voor elke wedstrijd voor het
thuisspelende team invullen of het winst/verlies/gelijkspel
wordt.
Op hoeveel manieren kun je zo'n formulier invullen? |
| |
|
|
|
| 4. |
Een beginnende popgroep heeft een
repertoire van 16 nummers, die ze bij een optreden allemaal gaan
spelen.
Hoeveel mogelijke "speelprogramma's" zijn
er met deze 16 nummers? |
| |
|
|
|
| 5. |
Op een piano zitten 83 toetsen. Ik ga
een melodietje spelen door 6 willekeurige toetsen na elkaar in
te drukken |
| |
|
|
|
| |
a. |
Hoeveel mogelijke melodietjes kan ik op die manier maken? |
|
| |
|
|
|
| |
b. |
Hoeveel mogelijke
melodietjes van 6 verschillende tonen kan ik maken? |
| |
|
|
|
| 6. |
Tien automobilisten
moeten hun auto gaan parkeren op 10 mogelijke parkeerplaatsen.
Op hoeveel verschillende manieren kan dat gebeuren? |
| |
|
|
|
| 7. |
We zijn met een groep van 8 mensen en
gaan lootjes trekken voor de komende Sinterklaasviering. Op
hoeveel verschillende manieren kunnen de lootjes worden
getrokken, als iemand ook zichzelf kan krijgen? |
| |
|
|
|
| 8. |
Een palindroom is een woord dat
hetzelfde is of je het nou gewoon leest of achterstevoren.
Voorbeelden zijn "parterretrap" en "koortsmeetsysteemstrook"
en "lepel"
Als we elke combinatie van letters een woord noemen (het hoeft
dus geen bestaand woord te zijn) hoeveel palindromen van 8
letters zijn er dan? |
| |
|
|
|
 |
|
|
© h.hofstede (h.hofstede@hogeland.nl)
|