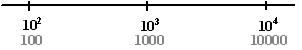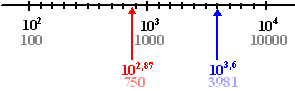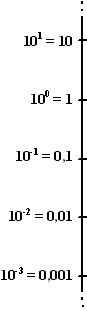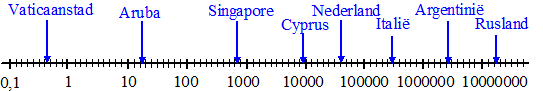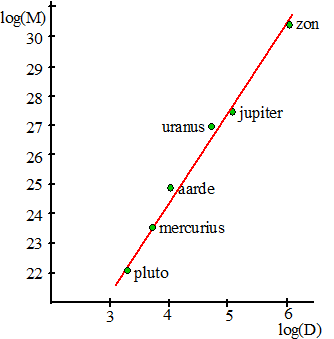
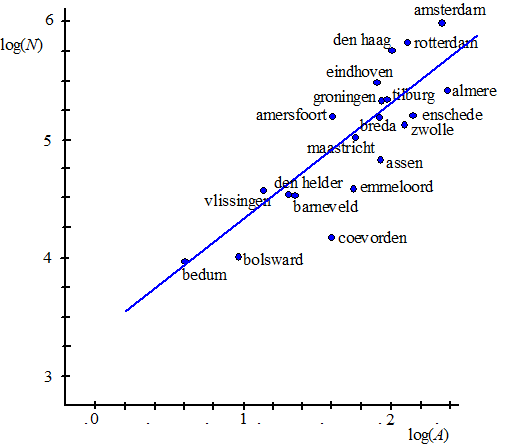
logaritmische schaal

	© h.hofstede (h.hofstede@hogeland.nl)

Logaritmische schaalverdeling.

Een beroemd verhaal vertelt dat de uitvinder van het schaakspel, ene Sissa ibn Dahir (zeg maar Sissa), het spel aan zijn koning leerde. Die was zó enthousiast dat hij de uitvinder een beloning wilde geven. "Zeg maar wat je wilt hebben," zei hij gul, want hij was namelijk nogal rijk. Sissa vroeg de koning om 2 graankorrels op het eerste veld van het schaakbord, 4 korrels op het tweede veld, 8 op het derde veld enzovoorts: steeds op een volgend veld het dubbele aantal van het vorige veld. 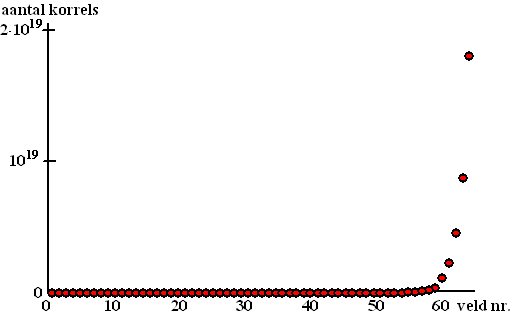De koning moest lachen om zo'n eenvoudige beloning.
Totdat hij een grafiek ging maken van het veldnummer op de x-as en het aantal graankorrels op de y-as......
Op zijn vel papier had hij een y-as tot een miljoen getekend. Maar daar paste zijn 20ste veld al niet meer op. (2²⁰ = 1048576) En op het vel dat hij er bovenaan plakte paste het 21ste veld al niet eens.
OEPS!
Het liep nogal uit de hand!!!!!
Om de hoogte van het laatste veld goed te tekenen zou hij ongeveer 2 • 10¹³ vellen papier boven elkaar nodig hebben. Als elk velletje 0,1 mm dik is, en je legt ze op elkaar als stapel zou die stapel maar liefst 2 miljoen km DIK zijn!!!!!!!!
Een grafiek op schaal zou er zó uitzien:

De eerste pakweg 55 velden geven een nogal saai beeld: daar is helemaal niets aan te zien. Om de saaiheid nog iets te verbergen heb ik er maar een lullig plaatje van Sissa naast gezet. En er valt uit al die stippen ook helemaal niets af te lezen. Je kunt bijvoorbeeld uit deze grafiek niet aflezen dat op het 30ste veld ongeveer een miljard korrels liggen.

Hoe krijgen we hier een "fatsoenlijke" grafiek uit?

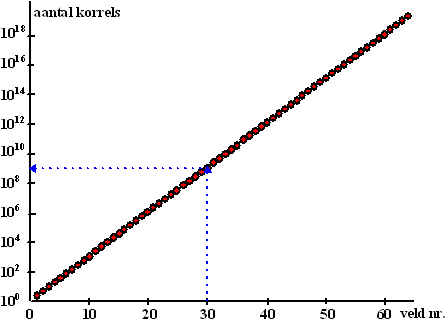
Een oplossing om die enorm grote getallen wat in de hand te houden is: zet op de y-as niet de getallen 1, 2, 3, ... maar de machten van 10: 10¹, 10², 10³, .... (dus 10, 100, 1000, ....). Dan wordt bovenstaande grafiek slechts zo'n 20 vakjes hoog en is er toch ook ruimte om de getallen op de eerste paar velden aan te geven. Kijk maar:

Nu is wel te zien welk aantal korrels ongeveer bij veld 30 en andere velden hoort. Veel beter!
Zo'n schaalverdeling waarbij dus niet de getallen zélf regelmatig oplopen, maar de machten van 10 heet een logaritmische schaalverdeling.

Logaritmische schaalverdeling: de machten van 10 zijn regelmatig.

Het is alsof de bovenste grafiek op elastiek of rubber is getekend, waarna de onderkant sterk is uitgerekt (hoe lager, hoe verder het rubber is uitgerekt) en de bovenkant niet. Zo'n schaalverdeling is dus erg handig als je in één grafiek zowel hele grote getallen als hele kleine getallen wilt aangeven.
Het vreemde papier hierboven heet enkellogaritmisch papier."Enkel" omdat er één as (in dit geval de y-as) zo vreemd veranderd is. De andere (x-as) is normaal.
Het beroemde filmpje ("Powers of Ten") hieronder geeft je een idee van hoe snel dat gaat op een logaritmische schaal.

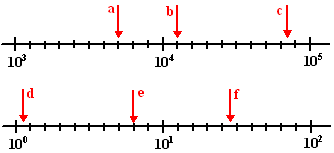
ONDERVERDELEN

Stel we hebben een logaritmische schaal waar dit een klein stukje van is (deze keer horizontaal getekend om papier te sparen):

En stel dat we nu het getal 750 op deze schaal willen aangeven. WAAR LIGT DAT?
Nou ja, natuurlijk daar ergens tussen 100 (10²) en 1000 (10³) maar waar?????
Denk om de hoofdregel:

De machten van 10 zijn regelmatig.

Dat betekent dat we 750 kunnen tekenen als we weten hoeveelste macht van 10 dat is.
Dus de vraag is 10^?= 750.
De oplossing is simpel: ? = ¹⁰log(750) = LOG(750) = 2,87
Verdeel het stuk tussen 100 en 1000 in deelstreepjes (10^2,1 - 10^2,2 - 10^2,3 - ...) en je hebt de plaats van 750:

Bij de rode pijl staat 750.
En net zo staat bij de blauwe pijl het getal 10^3,6 = 3981.

Je kunt het ook aangeven met "log" op de as

In plaats van de machten van 10^..... op de y-as te zetten kun je natuurlijk ook "log y" op de y-as zetten en dan kun je als die tienen weglaten en alleen de macht noteren.

Immers als y = 10³ dan is log(y) = log(10³) = 3
De rode en de blauwe schaalverdelingen hiernaast zijn daarom precies gelijk.

Twee vingeroefeningen tussendoor:

Vingeroefening 1: Geef op de logaritmische schaal hieronder de volgende getallen aan:

	a. 50	b. 900	c. 1100	d. 4500



Vingeroefening 2: Welke getallen horen bij de pijlen op de volgende logaritmische schalen?

HELP! Er is geen x-as!!

Als je wilt weten waar de x-as op jouw nieuwe schaalverdeling ligt, dan moet je dus oplossen 10^? = 0
Maar dat kan niet!!!!
"tien-tot-de-macht" kan nooit nul worden.

Kijk maar hiernaast: als je de machten van 10 laat afnemen tot -2, -3, -4 enzovoorts, dan worden de "echte" getallen kleiner en kleiner: 0.01, 0.001, 0.0001 enzovoorts. Het papier wordt verder en verder uitgerekt. NUL zal zo nooit worden bereikt.

Alhoewel er op zulk papier meestal wel een horizontale lijn met een schaalverdeling wordt getekend is het dus NIET de x-as. Die is er namelijk niet (hij ligt eigenlijk oneindig ver omlaag).

OPGAVEN

Op de volgende logaritmische schaal staat de oppervlakte (in km²) van een aantal landen.

Wat is de oppervlakte van Nederland?

Welke landen schelen meer in oppervlakte: Vaticaanstad en Cyprus of Nederland en Italië?

Hoeveel keer past Singapore ongeveer in Italië?

Hieronder staat een tabel met de hoogtes van verschillende objecten.
Maak een logaritmische schaalverdeling waarop deze hoogtes zijn weergegeven.

Object	Hoogte
Eiffeltoren	300 m
Mount Everest	8849 m
Verkeersdrempel	9 cm
Bouwlaag	2,6 m
Shanghai toren	632 m
Hoogspanningsmast	60 m

Hiernaast zie je van een aantal lichamen uit ons zonnestelsel de diameter (D, in km) en de massa (M, in kg)
Om ze allemaal goed in beeld te krijgen is log(M) uitgezet tegen log(D)

In de figuur is een rechte lijn getekend die goed bij deze punten past.

De dichtheid (in kg/m³) van een lichaam is gelijk aan de massa gedeeld door de inhoud. De inhoud kun je berekenen met de formule I = 0,25pD²

Bereken de dichtheid van de aarde.

Saturnus heeft een massa van 5,7×10²⁶ kg en een diameter van 121000 km.
Teken de plaats van Saturnus in de figuur hiernaast.

Het verband tussen D en M kan grofweg benaderd worden door de formule die past bij de lijn. Een formule daarvoor is : log M = 12,24 + 2,94 × log D

Neptunus heeft een massa van 1,0 × 10²⁶ kg

Bereken met behulp van de formule de diameter van Neptunus. Geef je antwoord in duizenden km nauwkeurig.

De formule kan geschreven worden als: M = a · D^b

Bereken a en b.

In de volgende figuur staan de gegevens van 20 woonplaatsen in Nederland in 2023.
Onderzocht is of er een verband bestaat tussen de oppervlakte A (in km²) en het aantal inwoners N van deze woonplaatsen. (Bron: https://allecijfers.nl)
In de figuur is een rechte lijn getekend die goed bij deze puntenwolk past.

Bereken het aantal inwoners van Vlissingen.

Eén van de woonplaatsen heeft een oppervlakte van 59 km² en een inwoneraantal van ongeveer 27000.
Leg uit welke woonplaats dat is.

In sommige gevallen is het aantal inwoners van een plaats met een bepaalde oppervlakte het dubbele van wat de lijn bij die oppervlakte aangeeft.
Voor die plaatsen geldt: log(N) = 0,99log(A) + 3,66

Geef in de figuur aan bij welke plaatsen het aantal inwoners meer is dan het dubbele van wat de lijn aangeeft.