| |
|
| |
©
h.hofstede (h.hofstede@hogeland.nl) |
|
|
De blokkendoos |
 |
| |
|
|
|
|
Losse
stukken en Lijm |
| |
|
|
|
Als een echte wiskundige een
formule (dat is een regel met letters en cijfers) ziet staan, dan ziet
hij nooit in ιιn keer de hele formule, maar hij ziet al wιl uit welke
blokjes de formule is opgebouwd. In ιιn oogopslag!
't Is eigenlijk net als bij een bouwwerk uit een bouwdoos: ook een ingewikkelde formule
is toch eigenlijk uit losse blokjes opgebouwd.
Ook jij kan dat leren want het is eigenlijk heel simpel (echt waar!)
De grote TRUC is: |
| |
|
|
|
PLUS en MIN
knipt de dingen los van elkaar.
KEER en GEDEELD DOOR plakt de dingen aan elkaar. |
|
| |
|
|
|
|
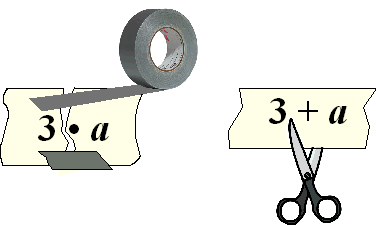 |
| |
|
|
|
Laten we een voorbeeldje nemen:
2 3 + 4 + 5 6 - 7 8 2 + 3 : 4
Een ervaren wiskundige ziet in deze formule
eigenlijk VIJF verschillende blokjes staan.
Jij ook???
Deze regel ziet er door de bril van een wiskundige zσ uit: |
| |
|
|
|
|
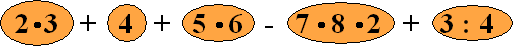 |
| |
|
|
|
|
Nog maar een voorbeeldje dan? Met letters erbij deze keer!
Hoeveel blokjes staan hier?
|
| 2 x + 3 + 5 y x
- 7
p + 8 - 4 : s |
|
ZES natuurlijk!!!
Tussen 2 en x staat niets, maar dat is eigenlijk "keer"
(er had net zo goed een stip kunnen staan)
Hetzelfde geldt tussen 5 en y en x: eigenlijk staat
daar 5 y x, dus dat is ιιn geheel.
Omgekeerd had de stip tussen 7 en p er net zo goed niet kunnen
staan.
Samengenomen ziet een wiskundige dus dit: |
| |
|
|
|
|

|
| |
|
|
|
|
Blokjes vereenvoudigen. |
| |
|
|
|
| Eerst maar even een
simpele bewering: |
| |
|
|
|
| bij
vermenigvuldigen doet de volgorde er niet toe. |
|
| |
|
|
|
Dat zul je vast wel
met mij eens zijn.
Immers 3 4 = 4 3 en ook 2 5 6 = 5 6 2 = 5
2 6 enz.
Deze simpele bewering heeft wel gevolgen voor onze blokkendoos!
Dat betekent dat we binnen ιιn blokje de volgorde zelf mogen bepalen.
In plaats van 2 x 3 mag je ook wel ook wel schrijven
2 3 x.
Omdat je ook hier zelf mag weten wat je
eerst doet, kun je dus best alvast 2 3 uitrekenen. Je kiest er
gewoon voor om dat eerst te doen.
Dan staat er namelijk in plaats van 2 3 x
ineens 6 x ofwel 6x en dat
ziet er een stuk eenvoudiger uit.
Conclusie:
|
| |
|
|
|
|
binnen ιιn blokje
mag je alvast alle getallen met elkaar
vermenigvuldigen.
(de letters daar kun je niks
mee, want je weet niet welk getal ze zijn) |
|
| |
|
|
|
|
Blokjes
samennemen. |
| |
|
|
|
| Soms kun je formules
vereenvoudigen door sommige blokjes samen te nemen. Daarvoor geldt: |
| |
|
|
|
|
Je mag blokjes samennemen als de
letters precies gelijk zijn |
|
| |
|
|
|
Dus bijvoorbeeld
2x + 3x kun je samennemen want die hebben beiden
alleen de letter x, maar 5a + 2x niet, want de
eerste heeft de letter a en de tweede de letter x.
Ook 2ab + 3a kun je NIET samennemen, want de
eerste heeft de letter a en de tweede ab, Dat is niet
precies gelijk! |
| |
|
|
|
Hoe gaat dat samennemen in z'n
werk?
Dat is heel eenvoudig.
Doe je bijvoorbeeld 5 keer "iets" plus nog 8 keer "iets" dan heb je in
totaal 13 keer "iets" gedaan. |
| |
|
|
|
|

|
| |
|
|
|
In die zwarte doos mag alles
zitten, zolang in alle dozen maar precies hetzelfde zit.
Als er x in zit, dan staat hier bijvoorbeeld 5x + 8x
= 13x. Maar als er ab in zit dan staat
hier 5ab + 8ab = 13ab.
Bedenk goed dat onze blokjes er zo uitzien: |
| |
|
|
|
|

|
| |
|
|
|
| Bij het samennemen van de twee
blokjes aan de linkerkant tel je dus de cijfers bij elkaar op, en je
schrijft de rest (de zwarte doos) ιιn keer over.
|
| |
|
|
|
Samennemen van
twee blokjes:
Tel de getallen bij elkaar op.
Schrijf de letters ιιn keer over. |
|
| |
|
|
|
En als er geen getal
staat?
Dan staat er eigenlijk het getal 1.
Dus 2a + a = 2a + 1a = 3a |
| |
|
|
|
Mintekens.
1. Tussen twee
blokjes in.
Natuurlijk komen er ook mintekens in wiskunde opgaven voor, maar weet je,
die zijn eigenlijk niet zo heel interessant!
Dat komt omdat MIN en PLUS eigenlijk hetzelfde is!
Kijk, de opgave 8 - 5 kun je ook lezen als 8 +
(-5)
Eigenlijk is er geen verschil tussen optellen en aftrekken. Aftrekken is
gewoon optellen maar dan met een negatief getal!
Voor letter-rekenen geldt dat dan natuurlijk ook.
6x - 4x kun je ook lezen als (6x) +
(-4x). Daar staan twee blokjes met precies dezelfde letter dus
die kun je samennemen. Je telt de getallen op (in dit geval 6 + -4 = 2)
en je schrijft de letter ιιn keer over. Dat geeft 6x
- 4x
= 2x.
Ik zal voor de duidelijkheid zo'n minteken tussen twee blokjes aangeven
met een groot minteken: -
en zo'n minteken van "negatief getal" met een klein minteken:
-
Je rekenmachine doet dat trouwens ook.
dingen van elkaar aftrekken:
-
negatieve getallen: (-) |

|
|
Voor letter-rekenen geldt dat dan natuurlijk ook.
6x - 4x kun je ook lezen als (6x) +
(-4x). Daar staan twee blokjes met precies dezelfde letter dus
die kun je samennemen. Je telt de getallen op (in dit geval 6 + -4 = 2)
en je schrijft de letter ιιn keer over. Dat geeft 6x
- 4x
= 2x.
En met meer blokjes gaat het precies zo: |
| |
|
|
|
|
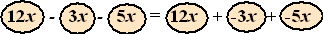 |
| |
|
|
|
Dat wordt dus 4x, want 12
+ (-3) + (-5) = 4.
Je ziet wel:
|
|
zo'n minteken hoort
eigenlijk bij het blokje waar hij direct vσσr staat. |
|
|
|
| |
|
|
|
| Mintekens binnen ιιn
blokje.
Dat is nog veel makkelijker. We hebben immers al
geleerd dat je binnen ιιn blokje alles mag uitrekenen wat je maar
kunt. Nou, dan hoef je alleen maar te weten dat:
|
|
min Χ min = plus
min Χ plus = min
plus Χ min = min |
|
|
|
| |
|
|
|
Dus bijvoorbeeld het blokje
(-2x 3y) kun je vereenvoudigen tot -6xy (want
-2 3 = -6)
En het blokje -4a -5b kun je
vereenvoudigen tot 20ab (want -4 -5 = 20)
En het blokje -3 p -2 -6 kun je
vereenvoudigen tot -36p (want -3 -2 -6 =
-36)KIJK GOED UIT: ιιn zo'n
stipje kan verschil maken: 2x - 3y
- 4xy kun
je niet verder vereenvoudigen want daar staan drie blokjes met
verschillende letters.
2x -3y - 4xy
kun je wιl vereenvoudigen, kijk maar: |
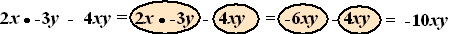 |
| |
|
|
|
| DIE ENE STIP MAAKT
NOGAL VERSCHIL! |
| |
|
|
|
Houd
dit goed uit elkaar!
Er zijn drie verschillende gevallen met "twee minnen". Kijk
hoe het met getallen gaat en hoe het (dus ook) met blokjes gaat: |
| |
|
|
|
| |
|
-3 - 4
= -7
2 - - 4 = 6
-2 -3 = 6 |
3x - 4x = -7x
2 - -4x = 6x
-2x -5 = 10x |
|
|
| |
|
|
|
| |
|
|
|
OPGAVEN. |
| |
|
|
|
| 1. |
Vereenvoudig zoveel
mogelijk. |
| |
|
|
| |
a. |
2a + 3 + 4a + 6 |
| |
|
|
| |
b. |
3x + 4x + 5 + 8 |
| |
|
|
| |
c. |
3m + 2n + 4m + 5 |
| |
|
|
| |
d. |
2x + 4x + 5 + x + 6 |
| |
|
|
| |
e. |
14a + 2b + b + 4 + 2a |
| |
|
|
| |
f. |
2m + 3mn + 4n + m + 5n |
| |
|
|
|
| 2. |
Vereenvoudig zoveel
mogelijk. |
| |
|
|
| |
a. |
2a 4 + 4 a 3 + 3 a |
| |
|
|
| |
b. |
x 5 + 6 + 4 x 2 + 8 |
| |
|
|
| |
c. |
2x 2 3 + 5 + 8 x |
| |
|
|
| |
d. |
p q 3 + q 5 p
+ 3p |
| |
|
|
| |
e. |
2abc + 3ab + 4bac + 4ba |
| |
|
|
| |
f. |
12 + 2xy + 3x 2y + 8 |
| |
|
|
|
| 3. |
Vereenvoudig zoveel
mogelijk. |
| |
|
|
| |
a. |
2 -x 4 - 6x |
| |
|
|
| |
b. |
-2p - 4p
-6 + 4 - p |
| |
|
|
| |
c. |
x -4 + 5x - x
- x -5 |
| |
|
|
| |
d. |
-2a
-b
-3
+ 4a -
3a
-b
-
a |
| |
|
|
| |
e. |
mn
-
4 5mn
-
2m
-3n
|
| |
|
|
| |
f. |
-4P
-Q
-
QP + 2P
-5
-
Q + 3Q
-
Q 7P |
| |
|
|
|
 |
|
|
© h.hofstede (h.hofstede@hogeland.nl)
|