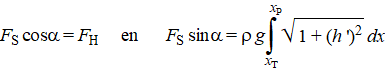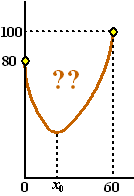De kettinglijn.

© h.hofstede (h.hofstede@hogeland.nl)

       
Even een makkelijk kwisje vooraf:   
 

wat is de overeenkomst tussen deze foto's en welke hoort en niet bij?
       

       
De overeenkomst is denk ik makkelijk:  het gaat steeds om hangende touwen/kabels/kettingen.
Welke hoort er niet bij?  Verrassend genoeg hoort geen één er niet bij. Waarschijnlijk dacht je die met die "poort"  maar wiskundig gezien is dat niet juist: al deze "kromme lijnen" hebben wiskundig gezien exact dezelfde vorm!!
       
Die vorm van zo'n hangende ketting noemen we een kettinglijn" (engels:  catenary, afkomstig van het Latijnse catena = ketting). Tijden lang dacht men dat het ging om een paraboolvorm. De beroemde Gallileï beweerde dat, dus dan geloof je dat waarschijnlijk wel.
Maar Galleileï had deze keer geen gelijk.  Joachim Jungius toonde door nauwkeurige metingen aan dat het geen parabool was. Christiaan Huygens liet door meetkundige theoretische overwegingen hetzelfde zien.
       
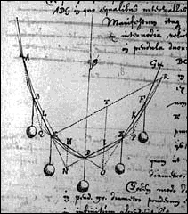
Op jacht naar de vergelijking.

Jakob Bernoulli had in de Acta Eruditorum (één van de eerste wetenschappelijke tijdschriften) aan de geleerde wereld de vraag voorgelegd, wat dan wél de vorm van een hangende ketting is. Een soort uitdaging.

Huygens, Leibniz en Johann Bernouilli wierpen zich op deze vraag..

Hiernaast zie je een deel van een manuscript van Huygens, die de vorm van een ketting met allemaal gewichtjes eraan bestudeerde. Hij gebruikte ontzettend ingewikkelde meetkundige methoden, maar kwam wel tot de goede oplossing.
Leibniz en Bernouilli gebruikten "nieuwere" methoden, met integralen en afgeleiden en dx en dy en zo, en vonden de oplossing op een eenvoudiger manier.

In ieder geval leverden deze heren in 1691 de juiste vergelijking van de kettinglijn, namelijk deze:
       

       
Daarin is a een constante die de schaal/de grootte van de kettinglijn bepaalt. Alle kettinglijnen zijn gelijkvormig. Dat kun je eenvoudig zien door die eerste a aan de rechterkant naar de linkerkant te brengen,
Dan staat er:    
Als je daarin x en y allebei door x/a en y/a vervangt verander je alleen de schaal van de figuur, niet de vorm.
 
Het is dus eigenlijk de vergelijking  y = 1/2 • (ex + e-x)

Hieronder zie je drie foto's van verschillende hangende kettingen. Je ziet dat de vorm inderdaad gelijk is, terwijl je aan de planken op de achtergrond mooi kunt zien dat de schaal nogal verschillend is.
       

       
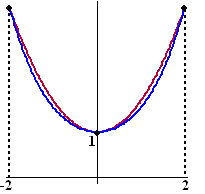
Hiernaast zie je hoe weinig deze kettinglijn van een parabool verschilt. Er staat een blauwe kettinglijn (met a = 1)  voor -2 < x < 2.

Die gaat door (0,1).

De rode grafiek is de parabool met dezelfde eindpunten en top.
Het scheelt niet veel, de kettinglijn "zakt net iets verder door".

Gallileï had zich maar een klein beetje vergist.....

       
De vergelijking van de kettinglijn.
       
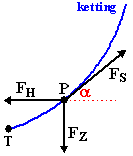
Hou je vast; hier komt een stukje natuurkunde.

Laten we een ketting bekijken, die oneindig dun is, en overal dichtheid r per cm heeft. Hiernaast is de rechterhelft van zo'n ketting getekend. In een willekeurig punt P werken nu drie krachten:

•  De spankracht FS waarmee het kettingdeel rechts van P onder hoek α omhoog trekt.
•  De zwaartekracht FZ ten gevolge van het gewicht van het kettingdeel TP
•  De spankracht FH waarmee het kettingdeel TP naar links trekt.

 
Als punt P in rust blijft moeten die drie krachten samen nul worden. Dat betekent dat de horizontale component van FS gelijk moet zijn aan FH, en de verticale gelijk aan  FZ.

Die horizontale component is FS • cosα. Verder is  FH een constante kracht. Het is de horizontale kracht waarmee beide kettinghelften in punt T aan elkaar trekken. Dus geldt  FS • cosα = FH.

De verticale component van FS  is gelijk aan FS • sinα  en moet gelijk zijn aan de zwaartekracht op deel TP. Die is gelijk aan FZ = mg = ρLg  waarbij ρ de dichtheid per cm van de ketting is, en g de zwaartekrachtversnelling.
De lengte L kun je met een integraal uitrekenen.  Als je de vergelijking van de ketting  h(x) noemt, dan geldt:
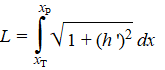Die formule wordt in deze les afgeleid. 

We komen dus terecht bij de volgende twee vergelijkingen (voor krachtevenwicht in horizontale en in verticale richting):

 

       
Het wordt pas echt interessant als je die twee op elkaar deelt:

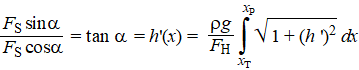Een interessant resultaat: die integraal daar rechts is de lengte van de grafiek! Daar staat dus:
 

h '  =  c • L
 
Daarbij is die ρG/FH dus een constante die van de grootte en van het gewicht van de ketting afhangt. Zoals je ziet hebben we hem  c genoemd.
Als je verder h' vervangt door y dan staat er   y = c ∫ √(1 + y2)dx   

Beide kanten de afgeleide nemen geeft dan   y' = c√(1 + y2)      (met dus y = h' ).
Dit is een eerste orde differentiaalvergelijking waarvan je de variabelen kunt scheiden en die door "eenvoudig" primitiveren is op te lossen.  Nou ja, zo heel eenvoudig is dat trouwens niet. Eigenlijk is het supermoeilijk. Als je een zondagmiddag over hebt, dan kun je het bewijs hiernaast misschien eens doorwerken.
 
Er komt uit  y = 1/2• (ecx - e-cx), 

Ik raad je wel aan dit niet zomaar te geloven maar het te controleren door deze functie te differentiëren en te laten zien dat er c√(1 + y2)  uitkomt. Wacht, daar maak ik een opgave van......
       
1. Toon aan dat de gegeven vergelijking voor y voldoet aan de differentiaalvergelijking
       

Maar y was gelijk aan h' , dus is  h'  =  1/2 • (ecx - e-cx) Om h te vinden moet je weer primitiveren:   h = 1/2c • (ecx + e-cx)  en daarmee is de vergelijking van de heren uit 1691 aangetoond (zij gebruikten trouwens de constante a = 1/c).
Natuurlijk moest bij dat primitiveren nog een constante, maar als we nemen dat die gelijk is aan 0, dan betekent dat, dat de ketting door het laagste punt  (0, 1/c) gaat.

       
Een rekenvoorbeeldje.

Neem een touw van 50 cm lang, dat opgehangen is aan twee even hoge punten die 30 cm uit elkaar liggen.
Bekijk de positieve helft van de kettingkromme.
Dan heeft de helft van dat touw lengte  L = 25 cm.
Maar h' = cL  dus als h'  = 1/2 • (ecx - e-cx)  dan moet dus gelden  c • 25 =  1/2 • (ecx - e-cx) en daarbij is x de horizontale afstand van dat halve touw, dus 15 cm.  Dat geeft  c • 25 =  1/2 • (e15c - e-15c)
Mijn grafische rekenmachine geeft dan  c = 0,1226, dus de vergelijking is  h = 4,08 • (e0,12x  + e-0,12x)
Het laagste punt van dat touw ligt dan  bij x = 0 en is dus  h = 8,16 cm.
De hoogste punten liggen bij x = ± 15 en dan is h = 25,36 cm.
       
       
2. Een ketting met lengte 80 cm wordt opgehangen aan twee even hoge punten, 40 cm uit elkaar.
       
  a. Geef de vergelijking van de kettinglijn die bij deze ketting hoort.
     

c = 0,1089 

  b. Bereken de helling van de kettinglijn in de ophangpunten.
     

± 4,36 

       
Ongelijke ophangpunten.
       
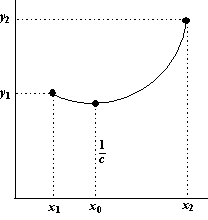
Als de ophangpunten niet even hoog zitten, wordt de situatie lastiger.
Stel dat de ophangpunten de punten (x1, y1) en (x2, y2) zijn.
Kies het assenstelsel weer zo, dat het laagste punt bij  y = 1/c zit  (dat was door de integratieconstante nul te kiezen, weet je nog?).

De plaats van dat laagste punt is nu nog niet bekend. Stel dat die plaats x0 is, dan is de vergelijking van de ketting lijn:  h(x) = 1/2c • (ec(x - x0) + e-c(x- x0))  want het is immers de normale kettinglijn x0 opzij geschoven.

Nu kun je twee vergelijkingen opstellen.

Op de eerste plaats moet de kettinglijn door de ophangpunten gaan.
Dat geeft  y1 = 1/2c • (ec(x1 - x0) + e-c(x1 - x0))
en op dezelfde manier  y2 = 1/2c • (ec(x2 - x0) + e-c(x2 - x0) )  
Trek die twee van elkaar af en je krijgt:
 y1 - y2 = Δy = 1/2c • (ec(x1 - x0) + e-c(x1 - x0) - ec(x2 - x0) - e-c(x2 - x0) )   ......(1)

       
Maar natuurlijk weet je ook de totale lengte L  van de ketting. Die bestaat nu uit twee delen:
L = 1/2c • (ec(x0 - x1) - e-c(x0 - x1) + ec(x2 - x0) - e-c(x2 - x0))   ........(2)

Dat zijn twee vergelijkingen (1) en (2)  met twee onbekenden  (x0 en c)
Maar die zijn niet zo eenvoudig op te lossen.....

Nou, weet je wat: dan proberen we gewoon wat!!!!!
•  gok een c.
•  dan kun je met (1) de waarde van x0 berekenen.
•  dan kun je met (2) de lengte van de ketting berekenen.
•  als die nog niet goed is, dan gok je een nieuwe c  (bedenk dat L groter wordt als c groter wordt)

Als je x0 en c hebt gevonden, moet je nog wel het touw "op de juiste hoogte hangen". Je hebt er  met je vergelijkingen voor gezorgd dat het hoogteverschil klopt.
Door bij h(x) een constante op te tellen kun je de echte ophanghoogte instellen.
   
Een rekenvoorbeeldje.

Een ketting van lengte 100 cm hangt tussen de punten (0, 80) en (60, 100).  Geef een vergelijking van de kettinglijn.

•  gok  c = 0,1.  Dan geeft (1)  dat  x0 = 29,003
•  Dan geeft (2)  dat  L = 201,354
•  Dat is te lang, dus we nemen c kleiner. Neem c bijvoorbeeld gelijk aan 0,05. 
   Dan geeft (1) dat  x0 = 24,346.
•  Dan geeft (2)  dat  L = 87,488.
•  Dat is te kort, dus c moet groter. Het zit al wel véél dichter in de buurt..
   Neem als volgende poging c bijvoorbeeld gelijk aan 0,055
•  Dan geeft (1) dat x0 = 26,043.
•  Dan geeft (2) dat L = 93,348.  bijna goed!
enz......... Dat wordt dan zoiets:

       
c 0,1 0,05 0,055 0,06 0,059 0,0598 0,0599 0,05995 0,05994  
x0 29,003 25,346 26,043 26,624 26,516 26,603 26,614 26,619 26,618 ....
L 201,354 87,488 93,348 100,091 98,667 99,803 99,946 100,019 100,004 ....
       
 
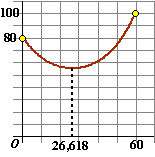
De uiteindelijke waarde wordt ongeveer c = 0,05994 en dat geeft L = 100,004 en x0 = 26,618

Maar dat geeft  h(0) = 41,333, dus er moet nog 80-41,333 = 38,667 bij opgeteld worden om in het punt (0,80) te beginnen.
Dat geeft uiteindelijk:
Hiernaast zie je een plot daarvan.
       
             
3. Een ketting van lengte 150 cm hangt tussen de punten (0, 120) en (60, 90). 
Geef een vergelijking van de kettinglijn.
             
De kabel van een hangbrug.
       
De vergelijkingen tot nu toe gingen allemaal over een ketting of touw dat vrij hangt, met alleen het eigen gewicht. Bij heel veel hangbruggen, zoals bijvoorbeeld de beroemde Golden Gate brug in San Francisco hieronder, hangt er een heel wegdek aan de kabel.
   

   
Wat verandert er in dat geval aan het verhaal hierboven?

Nou, meestal is dat wegdek vele malen zwaarder dan de kabel zelf, dus het gewicht van de kabel kun je verwaarlozen.
In het krachtenverhaal hierboven geldt dan nog steeds dat FZ = mg = rLg
 Maar dan is die L niet de lengte van het touw, maar de lengte van het wegdek!!!
En dat is alleen afhankelijk van de horizontale afstand van P to T,
dus gelijk aan c • x

 
     
Dat geeft de veel eenvoudiger vergelijking  h'(x) = c • x
De oplossing daarvan is  h = 1/2cx2  + d
Kortom:
 

dan is het wél een parabool.
       
       
De kettinglijn kom je ook tegen bij constructies waarbij de ketting "op de kop" staat. Boogvormen dus.
Een kettinglijn op z'n kop geeft de stevigste boog. Het idee daarachter is het volgende.

In een vrij hangend touw zijn er alleen maar trekkrachten aanwezig. (als er andere krachten waren ging het touw wel anders hangen). En al die trekkrachten zijn in de richting van het touw. Als je die vorm omkeert, dan zullen er dus alleen maar drukkrachten in de richting van de nieuwe vorm zijn. Ofwel: er zijn geen vervelende extra drukkrachten naar buiten of naar binnen die scheuringen of barsten kunnen veroorzaken.

Logisch toch?
 
De beroemde architect Gaudi gebruikte kettinglijnen bij het ontwerpen van de bogen van de beroemde Sagrada Familia in Barcelona. (zie hiernaast).

Een zéér (zéér, zéér) uitgebreide analyse van de gebruikte technieken vind je hier.

Hieronder zie je nog een paar afbeeldingen van beroemde "omgekeerde kettinglijnen".

 

 
       

       
       

© h.hofstede (h.hofstede@hogeland.nl)