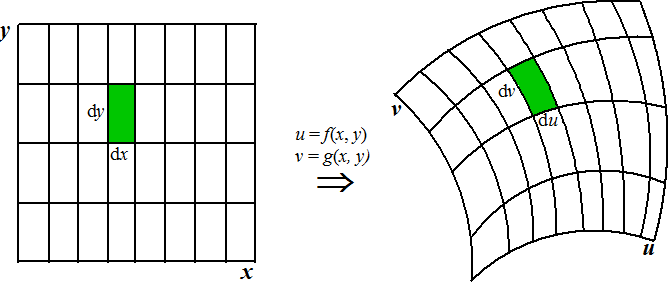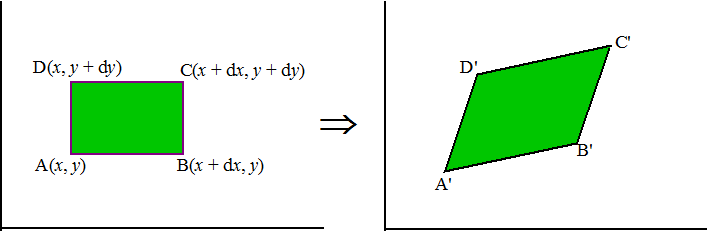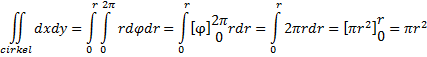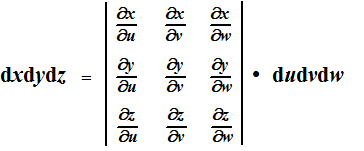Jacobiaan

© h.hofstede (h.hofstede@hogeland.nl)

De Jacobiaan.

Deze les gaat erover als we bij een dubbelintegraal met y en x overgaan op nieuwe variabelen u en v.
De hoofdvraag daarbij is:

Hoe zit dat dan precies met die dydx?

Laten we zeggen dat voor de nieuwe variabelen geldt u = f(x, y) en v = g(x, y) met f en g willekeurige functies.
Het rooster van vierkantjes met zijden dx en dy zal dan overgaan in een nieuw rooster met "gebiedjes" du en dv.
Als we dx en dy maar klein genoeg kiezen, (en als de functie f en g niet al te "raar" zijn) dan zullen die nieuwe gebiedjes er uitzien als parallellogrammetjes. De eventueel gekromde randen zijn dan bij benadering rechte lijnstukken.

De oppervlakte van een parallellogram.

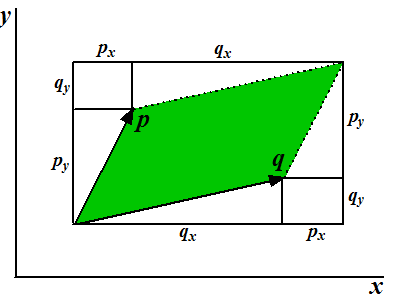
Laten we een willekeurig parallellogram bekijken dat wordt opgespannen door de twee vectoren p en q met kentallen p_x, p_y en q_x, q_y zoals in de figuur hiernaast.

De oppervlakte van het parallellogram vind je door van de grote rechthoek vier driehoeken en twee rechthoeken af te trekken:

(p_x + q_x)(p_y + q_x) - q_xq_y - p_xp_y - 2p_xq_y
= p_xp_y + p_xq_y + q_xp_y + q_xq_y - q_xq_y - p_xp_y - 2p_xq_y
= q_xp_y - p_xq_y

Als p en q een andere kant op staan dan komt daar nog steeds hetzelfde uit, maar het moet wel positief zijn (is immers een oppervlakte. Als je dat niet gelooft dan teken vooral allerlei situaties zelf maar uit.

Daar komt elke keer weer diezelfde oppervlakte uit.

oppervlakte parallellogram = q_xp_y - p_xq_y

dydx omzetten in dudv

Stel dat een rechthoek ABCD met lengte en breedte dx en dy waarvan punt A de coördinaten (x, y) heeft door deze verandering van variabelen overgaat in een parallellogram A'B'C'D'

Dan geldt:
A' = (f(x, y), g(x, y))
B' = (f(x + dx, y), g(x + dx, y))
D' = (f(x, y + dy), g(x, y + dy))

Maar f(x + dx, y) is gelijk aan f(x, y) + ^∂^f/_∂_x • dx immers de afgeleide ^∂^f/_∂_x zegt hoe snel f verandert als x verandert.
En op dezelfde manier geldt dan:
f(x, y + dy) = f(x, y) + ^∂^f/_∂_y • dy en g(x, y + dy) = g(x, y) + ^∂g/_∂_y • dy en g(x + dx, y ) = g(x, y) + ^∂g/_∂_x • dx

In het rechterplaatje zie je twee vectoren A'B' en A'D' die een parallellogram opspannen.
Voor de oppervlakte van zo'n parallellogram geldt dan (volgends de eerder gevonden regel):
O = (A'B')_x • (A'D')_y - (A'D')_x • (A'B')_y
O = (A_x - B_x) • (A_y - D_y) - (A_x - D_x) • (A_y - B_y)
O = ^∂^f/_∂_x • dx • ^∂g/_∂_y • dy - ^∂^f/_∂y • dy • ^∂^f/_∂_x • dx
O = ( ^∂u/_∂_x • ^∂v/_∂_y - ^∂u/_∂y • ^∂v/_∂_x ) • dxdy

Je ziet dat een oppervlakte dxdy bij zo'n transformatie overgaat in een oppervlakte dudv waarvoor geldt:

dudv = (^∂^u/_∂_x • ^∂^v/_∂_y - ^∂^u/_∂_y • ^∂^v/_∂_x ) • dxdy

Dat deel tussen die haakjes heet ook wel de Jacobiaan.

Meest voorkomende toepassing: poolcoördinaten.

Als je van gewone coördinaten (x, y) overstapt op poolcoördinaten (r, φ) Dan geldt:
x = rcosφ en y = rsinφ, dus φ = arctan(^y/_x) en r = √(x² + y²)
Omdat de afgeleide van arctan(x) gelijk is aan ¹/_{(1
+ x²)}geldt dan (met de kettingregel uiteraard):

Dat betekent dat drdφ = ¹/_r • dxdy ofwel dxdy = r • drdφ

wacht... dat kan handiger.....
Je kunt de hele afleiding van die Jacobiaan natuurlijk net zo goed (x, y) en (u, v) met elkaar verwisselen. Als je van een rechthoekje dudv naar een parallellogrammetje dxdy gaat, dan geldt volgens precies dezelfde afleiding:

dxdy = (^∂^x/_∂_u • ^∂^y/_∂_v - ^∂^x/_∂_v • ^∂^y/_∂_u ) • dudv

x = rsinφ   en   y = rcosφ geeft veel makkelijkere afgeleides:
^∂^x/_∂r = sinφ en   ^∂x/_∂j = rcosφ en   ^∂y/_∂r = cosφ en   ^∂y/_∂j = - rsinφ
De Jacobiaan is dan   rcosφ • cosφ - - rsinφ • sinφ = rcos²φ + rsin²φ = r(cos²φ + sin²φ) = r
Dus dxdy = r • drdφ      Gelukkig dezelfde conclusie.

poolcoördinaten:
dxdy = rdrdφ

Laten we voor de grap meteen maar even in één regel de oppervlakte van een cirkel uitrekenen:

Hogere dimensies.

Als je integralen in nog hogere dimensies gaat berekenen (zullen we later met drievoudige integralen gaan doen) dan krijg je elke keer ook te maken met zo'n Jacobiaan.
Voor drie dimensies ziet die er als volgt uit:

Nou ja, dan kun je vast zelf wel verzinnen hoe dat vierdimensionaal eruit zal zien, en vijfdimensionaal, en zesdimensionaal, ....