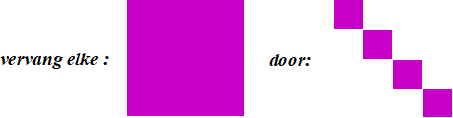fractale dimensie

© h.hofstede (h.hofstede@hogeland.nl)

De dimensie van een fractal.

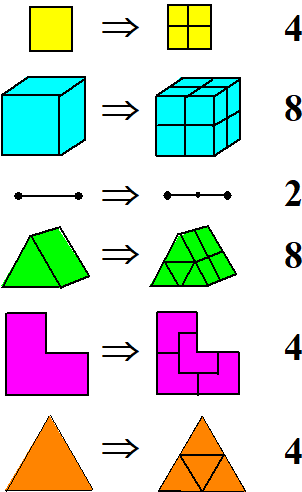
Laten we eens gaan tellen in hoeveel exemplaren, die allemaal de helft van de oorspronkelijke afmetingen zijn, je zo'n zelfgelijkende figuur kunt onderverdelen.
Voor het gemak doen we dat even voor erg simpele zelfgelijkende figuren.

Hieronder staat een aantal zulke eenvoudige zelfgelijkende figuren getekend.
Rechts van elke figuur staat steeds aangegeven staat hoeveel kleineren nodig waren om die eerste te maken.

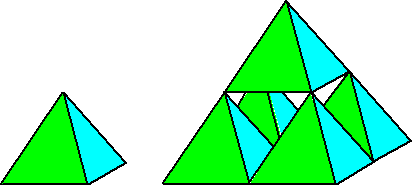
Valt hier iets op te merken?

Oké, daar rechts staan de getallen 2, 4 en 8. Ik hoop dat het volgende je opvalt:
Þ 2 staat bij de enige ééndimensionale figuur (de lijn)
Þ 4 staat bij de tweedimensionale figuren (de driehoek, het vierkant en de L-vorm)
Þ 8 staat bij de driedimensionale figuren (de kubus en de piramide).

Het lijkt erop dat de volgende regel van toepassing is:
Als de dimensie D is, dan verdeel je een figuur in 2^D kleinere figuren die de helft zijn.

Dat is ook eigenlijk wel logisch.
Als je een lijnstuk dubbel zo groot maakt, dan gebeurt dat in één richting (dimensie). Bij een vierkant gebeurt dat in twee richtingen (lengte en breedte) dus daarvoor zijn er 2 × 2 = 4 kleineren nodig. Bij een kubus gebeurt dat verdubbelen in drie richtingen (dimensies) dus daarvoor zijn 2 × 2 × 2= 8 kleineren nodig.

Deze manier om een dimensie te definiëren komt van de Duitse wiskundige Felix Hausdorff en heet dan ook wel de Hausdorff Dimensie.

Je kunt het ook nog ruimer bekijken. De kleinere figuren hoeven nier per se de helft te zijn. Je kunt een vierkant ook verdelen in vierkantjes die ¹/₃ zijn, dan heb je er 9 nodig, en 9 = 3² (9 = aantal, 3 is verkleining, 2 = dimensie)

Als je een figuur verdeelt in delen die elk factor ¹/f zijn,
en je hebt daarvoor n zulke figuren nodig,
dan geldt voor de dimensie D:
n = f ^D

Je kunt dat trouwens nog makkelijk veranderen in D = ^logn/_logf

Maar hoe is dat bij fractals?

Bij de Sierpinski driehoek zijn er steeds 3 figuren nodig van de halve grootte.
Dat betekent dat zou gelden 2^D = 3 en dat is zo voor D = 1,58490....
Dat betekent dat de Sierpinski-driehoek een 1,58-dimensionale figuur is!!

Een Koch-kromme heeft als recept:

Je ziet dat er nu 4 nieuwe lijnstukken nodig zijn, maar dat die allemaal ¹/₃ van de oorspronkelijke zijn.
4 = 3^D geeft D = 1,26185...

Je ziet: fractals hebben niet simpelweg een dimensie 1, 2 of 3. Er zijn allerlei tussenvormen mogelijk. Zo is er bijvoorbeeld een lijn-fractal (ééndimensionaal zou je zeggen?) die een vlak helemaal kan vullen (dus tóch tweedimensionaal?)

In de volgende les behandelen we nog een andere aanpak om dimensies van figuren vast te stellen.

OPGAVEN

Bereken de dimensie van de draak-kromme uit deze les.

Wat valt hieruit te concluderen?

Iemand ontwerpt een ruimtelijke fractal op de volgende manier door piramides te stapelen, een soort ruimtelijke versie van de Sierpinski driehoek:

Bereken de dimensie van deze fractal.

2,32.

"Cantor-stof" is een fractal met recept:

a. Bereken de dimensie van Cantor-stof.

1,26.

b. Hoe verandert de dimensie als je bij de vier vierkantjes er nog eentje in het midden toevoegt?

1,46.

Iemand ontwerpt een fractal met de regel:

Bereken de dimensie van deze fractal en verklaar je antwoord.

D = 1.