| |
© h.hofstede (h.hofstede@hogeland.nl)
|
|
|
Variabele grenzen. |
| |
|
|
|
In de vorige les over
dubbelintegralen hadden we steeds als integratiegebied een mooi
rechthoekig stuk, evenwijdig aan de assen, ofwel, x en y
lagen beiden tussen vaste grenzen.
Ook als dat niet zo is, kunnen we methode van de vorige les blijven
gebruiken, maar dan moeten we alleen goed oppassen wat de
integratiegrenzen zijn. |
| |
|
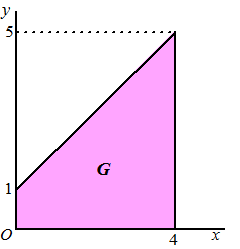 |
voorbeeld.
Neem de functie f(x, y) = x + 2y
die we willen integreren over het driehoekige gebied G hiernaast.
De bovenrand van G wordt gegeven door de lijn y = 1
+ x, maar dat had je vast al wel gezien.
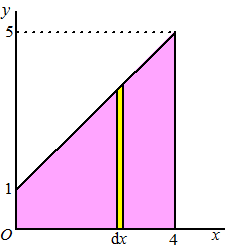
Dan zou je eerst ergens een stukje dx kunnen kiezen, en dan bij
die x de integraal van alle y-waarden kunnen berekenen. |
Je berekent dan de
integraal dy over het gele strookje hiernaast.
Maar bedenk daarbij goed dat de y loopt van 0 tot de
bovenrand, dus dat is van 0 tot x + 1
Dat geeft voor de integraal: |
 |
|
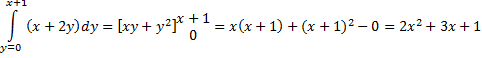 |
| |
|
| Dit laatste resultaat
moet je vervolgens weer integreren over dx, nu voor x van
0 tot 4: |
|
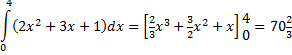 |
| |
|
|
|
|
Andersom kan nog steeds! |
| |
|
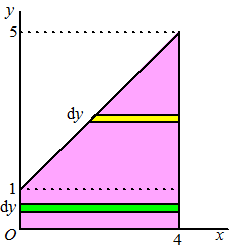 |
Als je eerst de x
wilt integreren dan is dat wat lastiger, want bij sommige y-waarden
loopt x van 0 tot 4, en bij anderen van de bovenrand tot 4.
Tussen y = 0 en y = 1 heb je van die groene strookjes
waarbij x van 0 tot 4 loopt.
Tussen y = 1 en y = 5 heb je van die gele strookjes
waarbij x van de schuine lijn tot 4 loopt. Die schuine lijn
is y = 1 + x dus x = y - 1
Daarom moet je de integraal nu in twee delen splitsen: |
|
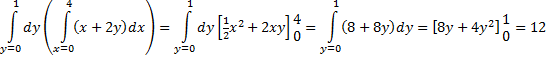 |
|
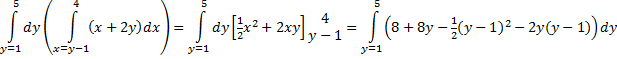 |
| |
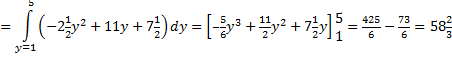 |
Samen geeft dat
12 + 582/3
= 702/3.
Nou, dat klopt dan tenminste weer..... |
| |
|
 |
|
Gekromde grenzen. |
| |
|
Het gebied waarover we integreren
kan natuurlijk ook best door krommen worden ingesloten. De aanpak blijft
hetzelfde als hierboven. Een voorbeeldje zal wel genoeg zijn, denk
ik.
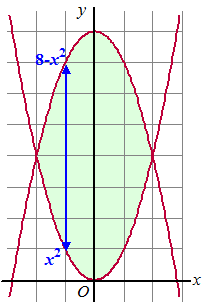
Stel dat we de functie z = 2x + y willen
integreren over het gebied dat wordt ingesloten door de parabolen
y = x2 en y = 8 - x2
hiernaast.
Je ziet dat x dan van -2 tot 2 loopt.
Maar bij één bepaalde x loopt y van x2
tot 8 - x2 (zie de blauwe lijn)
Dat geeft de volgende oplossing: |
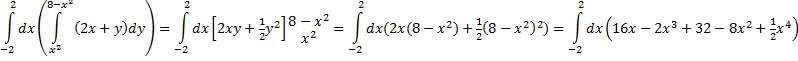 |
| [8x2 -
1/2x4
+ 32x - 8/3x3
+ 1/10x5
]2-2 = 1048/15 -
- 1408/15 = 2456/15 |
| |
Merk nog even op dat je rustig moet uitzoeken
hoe je die blauwe pijl in de figuur tekent. Hier was verticaal erg
makkelijk (steeds dezelfde functies als grenzen). Bij een gebied dat aan
de zijkanten wordt ingesloten door twee krommen zal vaak een horizontale
blauwe lijn makkelijk werken.
Ach, soms kan zelfs allebei en kun je kiezen! Altijd leuk om zulke
opgaven op twee manieren te doen en te kijken of er het zelfde uitkomt!
Tenminste dat vind ík wel.....De kick als het weer klopt...... |
|
|
| |
|
|
|
|
OPGAVEN |
| |
|
|
|
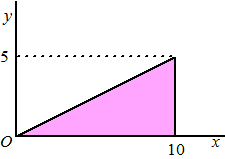
| 1. |
Bereken de integraal
van f(x, y) = xy over het
gebied hiernaast. |
 |
| |
|
|
|
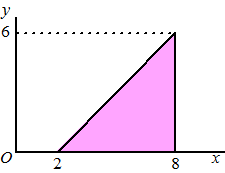
| 2. |
Bereken de
integraal van f(x, y) = y + x2
over het gebied hiernaast. |
 |
| |
|
|
|
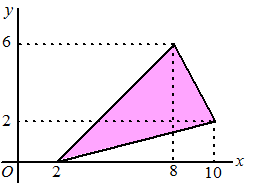
| 3. |
Bereken de
integraal van f(x, y) = y + x
over het gebied hiernaast. |
 |
| |
|
|
|
| 4. |
Bereken het
volume van het lichaam onder de grafiek van
z = x2 + y2
met als grondvlak het gebied ingesloten door de grafieken
van y = x en y = x2 |
| |
|
|
|
| |
|
|
|
| 5. |
Bereken de
integraal van de functie f(x, y) = xy
over het gebied, ingesloten door de parabool
y2 = x + 2 en de lijn y =
x |
| |
|
|
|
| |
|
|
|
| |
|
|
 |
|
|
© h.hofstede (h.hofstede@hogeland.nl)
|