| |
© h.hofstede (h.hofstede@hogeland.nl)
|
|
De kortste route.
- Dijkstra's Algoritme- |
| |
|
|
|
Een gewogen graaf is
een graaf waarvan aan de verbindingslijnen getallen zijn verbonden. Je
zou het kunnen zien als de afstanden in kilometers.
Een interessante vraagt is dan natuurlijk "Wat is de kortste
afstand tussen A en B?"
Nou heeft de Nederlander Edsger Dijkstra daar al in 1959 een slimme
methode voor bedacht. En die heet dan ook sindsdien Dijkstra's
Algoritme. Je komt het trouwens ook wel tegen onder de naam
driekleuren-algoritme, omdat er steeds drie soorten knooppunten zijn:
huidige, bezochte en niet-bezochte.
Het algoritme werkt als volgt: |
| |
|
|
|
| A. |
Geef de beginknoop
voorlopig afstand 0 (dat noemen we de huidige knoop) en
alle andere knopen voorlopige afstand ∞
(die noemen we niet-bezochte knopen).
|
| B. |
Bekijk alle directe
buren van de huidige knoop. Voor elk van die knopen kun je twee
afstanden vinden:
1. de voorlopige afstand die er al bij staat
2. de voorlopige afstand van de huidige knoop plus de lengte van
de verbindingslijn vanaf de huidige knoop naar deze
Kies de kortste afstand van beiden. Dat wordt de nieuwe voorlopige
afstand van deze knoop. |
| C. |
Als je alle
buurknopen hebt gehad wordt de huidige knoop nu een
bezochte knoop.
Kies als nieuwe huidige knoop de knoop met de kleinste voorlopige
afstand.
Ga weer naar stap B. |
| |
|
|
|
|
Voorbeeldje: |
| |
|
|
|
|
 |
| |
|
|
|
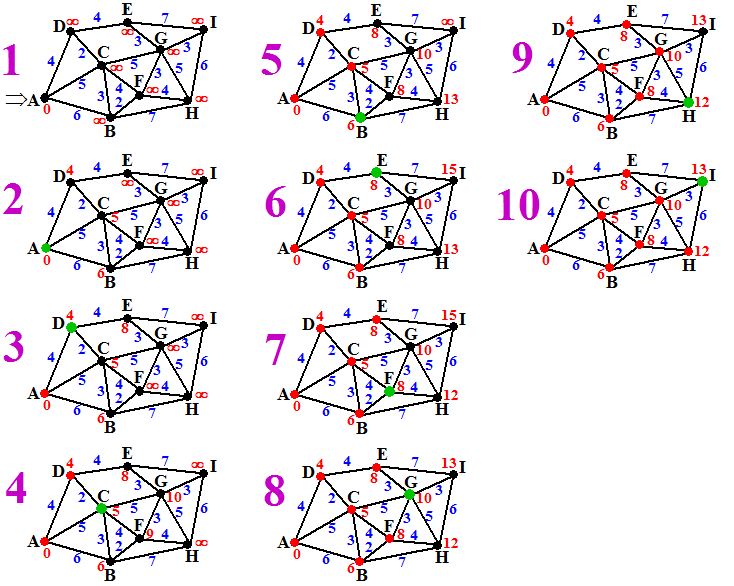
| In deze plaatjes 1 tm
10 zie je hoe je het in zijn werk gaat. De groene knoop is de huidige,
de rode zijn bezochte knopen, de zwarte zijn niet-bezochte knopen. De
blauwe getallen geven de lengte van de verbindingslijn, de rode getallen
geven de voorlopige kortste afstand tot de knoop. |
| |
|
|
|
| 1. |
Kies A als
startknoop, geef die afstand 0, en
alle anderen afstand ∞ |
| 2. |
De buren B, C, D
krijgen afstanden 6, 5, 4. |
| 3. |
A wordt een bezochte
knoop, D wordt de huidige knoop. E wordt 4
+ 4 = 8.
C zou 4 + 2
= 6 worden, maar dat is meer dan
5 dus C blijft
5. |
| 4. |
D wordt een bezochte
knoop, C wordt de huidige knoop. G wordt 5
+ 5 = 10,
F wordt 5 +
4 = 9,
B zou 5 + 3
= 8 worden, maar is al
6, dus blijft
6. |
| 5. |
C wordt een bezochte
knoop, B wordt de huidige knoop. F wordt
6 + 2
= 8, H wordt
6 + 7
= 13 |
| 6. |
B wordt bezochte
knoop, E wordt de huidige knoop. I wordt
8 + 7 =
15. G zou
8 + 3
= 11 worden, maar is al
10 dus blijft
10. |
| 7. |
E wordt bezochte
knoop, F wordt huidige knoop. H wordt 8
+ 4 = 12.
G zou 8 + 3
= 11 worden, maar is al
10 dus blijft
10. |
| 8. |
F wordt bezochte
knoop, G wordt huidige knoop. I wordt 10
+ 3 = 13.
H zou 10 +
5 = 15 worden, maar is al
12, dus blijft
12. |
| 9. |
G wordt bezochte
knoop, H wordt huidige knoop. I zou 12
+ 8 = 18
worden, maar is al 13, dus blijft
13. |
| 10. |
KLAAR! |
| |
|
|
|
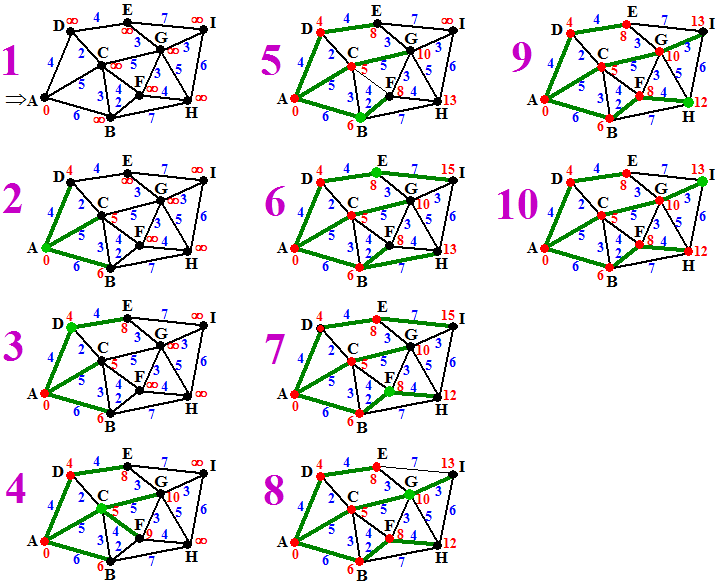
Op deze manier vind
je van alle andere knopen de minimale afstand tot knoop A. Merk
nog even op dat je niet vindt welke route die afstand oplevert.
Als je die "beste routes" ook wilt weten kun je elke keer
als je het getal van een knoop verandert de verbindingslijn die dat
oplevert kleuren, en de eventuele anderen die al gekleurd zijn weer
zwart maken.
Hieronder geeft dat de groene optimale routes (ga zelf maar na). |
| |
|
|
|
|
 |
| |
|
|
|
|
OPGAVEN |
| |
|
|
|
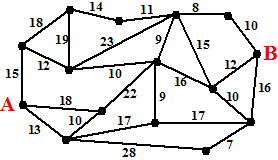
| 1. |
Zoek met behulp van
Dijkstra's algoritme de kortste verbinding tussen A en B in de graaf
hiernaast. |
 |
| |
|
|
|
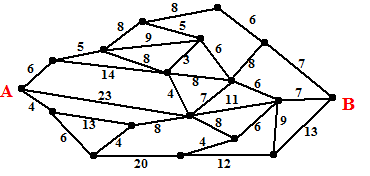
| 2. |
Zoek met behulp van
Dijkstra's algoritme de kortste verbinding tussen A en B in de graaf
hiernaast. |
 |
| |
|
|
|
| |
|
|
 |
|
© h.hofstede (h.hofstede@hogeland.nl)
|