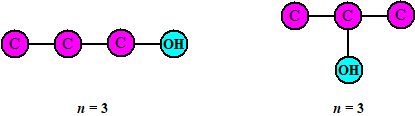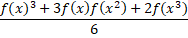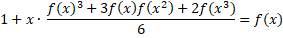aliphatische alcoholen

© h.hofstede (h.hofstede@hogeland.nl)

Koolstofketens.

In deze les over permutatiegroepen leerden we over de cykelindex, en hoe je die kunt gebruiken om aantallen mogelijke permutaties te tellen. Even een klein minivoorbeeldje om je geheugen op te frissen en om op voort te borduren:

Stel je hebt rode, groene en blauwe knikkers en die wil je op de hoekpunten van een gelijkzijdige driehoek leggen. We beginnen eenvoudig door te eisen dat we alleen de identieke permutatie toestaan. Dat betekent dat we alle anderen als verschillend van elkaar zien, dus dat in de cykelindex alleen f₁³ voorkomt.
Als je je afvraagt hoeveel mogelijkheden er nu zijn met bijvoorbeeld 2 rode knikkers, dan gaat dat zo:

(r + g + b) invullen geeft (r+ g + b)³ = r³ + g³ + b³ + 3r²g + 3r²b + 3g²r+ 3g²b + 3b²r + 3b²g + 6rbgdus bijvoorbeeld lees je snel af uit deze coëfficiënten:

•

met 2 rood en 1 blauw zijn er 3 mogelijkheden (de coëfficiënt van 3r²b) maar dat wist je natuurlijk zó ook wel: je kunt degene die je blauw kleurt uit 3 kiezen.

•

met 2 verschillende kleuren zijn er 18 mogelijkheden (al die coëfficiënten 3 samen)

•

in totaal zijn er 27 mogelijkheden: dûh, voor elk hoekpunt 3, dus 3³ . Logisch.

Verdieping 1.

Maar nou komt het idee. Als we nou in plaats van knikkers geen knikkers maar groepjes knikkers op de hoekpunten gaan leggen......

We zijn een hele nacht druk geweest en hebben een aantal nieuwe knikkers gemaakt door anderen aan elkaar te lijmen. Zo hebben we nu een pot met RB knikkers, een pot met BB knikkers en nog losse G knikkers, zoals hieronder.

Als ik nu weer zulke "knikkers" op de hoekpunten van een driehoek zou leggen, dan zou ik zulke vreemde driehoeken kunnen krijgen:

Noem eerst RG even X en BB even Y.
Dan krijg je voor de cykelindex:
(X + Y + g)³ = X³ + Y³ + g³ + 3X²Y + 3X²g + 3Y²X + 3Y²g + 3g²X + 3g²Y + 6XYg

En nou komt de grote truc: als je van je eindresultaat wilt weten hoeveel rode, blauwe en groene knikkers er nou in totaal zijn gebruikt, dan vervang je de X gewoon door rb en die Y door bb
Dan staat er:

(X + Y + g)³
r³b³ + b³b³ + g³ + 3r²b²bb + 3r²b²g + 3b²b²rb + 3b²b²g + 3g²rb + 3g²bb + 6rbbbg
= r³b³ + b⁶ + g³ + 3r²b³ + 3r²b²g + 3b⁵r + 3b⁴g + 3g²rb + 3g²b² + 6rb³g

En nou kun je weer direct zien dat er bijvoorbeeld 3 manieren zijn met 2 rode, 2 blauwe en een groene knikker: de coëfficiënt van 3r²b²g. Je hoeft je niet meer druk te maken om de manieren waarop dat tot stand kan komen (alhoewel je vast wel ziet dat het die rechterdriehoek hierboven met zijn neefjes is).

Verdieping 2.

Een tweede mogelijkheid zou zijn, dat er van één kleur verschillende soorten knikkers zijn. Stel bijvoorbeeld dat er ronde, vierkante en driehoekige rode knikkers zijn.
De cyklindex gaf (r+ g + b)³ = r³ + g³ + b³ + 3r²g + 3r²b + 3g²r+ 3g²b + 3b²r + 3b²g + 6rbgMaar elke term met een r erin staat nu eigenlijk voor 3 verschillende mogelijkheden, want der kan rond, vierkant of driehoekig zijn. En elke term met r² staat voor 9 mogelijkheden: drie voor de eerste r en drie voor de tweede.
Je zult al wel doorhebben dat we daar rekening mee kunnen houden door r te vervangen door 3r:
(3r+ g + b)³ = 27r³ + g³ + b³ + 27r²g + 27r²b + 9g²r+ 3g²b + 9b²r + 3b²g + 18rbg

Een belangrijke toepassing: Aliphatische Alcoholen.

Aliphatische alcoholen zijn alcoholen met moleculeformule C_nH_{2n
+ 1}OH. Het gaat ons erom welke structuurformules (woord zegt het al; welke ligging ten opzichte van elkaar de atomen hebben) bij welke n horen.
Voor het gemak teken ik in het vervolg niet al die H's meer. Omdat we weten dat aan elke C vier dingen moeten zitten is voldoende om de H's er verder steeds bij te denken als je dat wilt.

Voor n = 1 en n = 2 ziet dat er zó uit:

Voor n = 3 ontstaat er voor het eerst wiskundig iets interessants: er zijn twee verschillende mogelijkheden (twee isomeren)

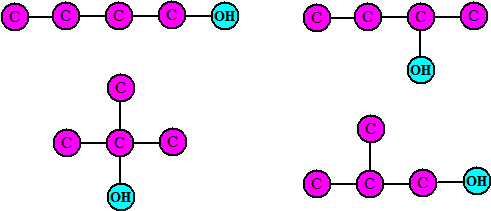
De vraag is: hoeveel isomeren horen er bij een bepaalde n? Dat lijkt op het eerste gezicht misschien makkelijk, maar vergis je niet: die koolstofatomen hoeven niet meer in een mooie rechte lijn te blijven liggen zoals tot nu toe!
Voor n = 4 zijn er daarom al 4:

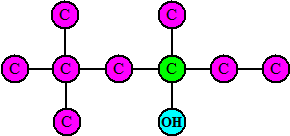
Zo'n structuur als hierboven heet in de grafentheorie een boom (er mogen geen lussen in zitten en hij moet helemaal aan elkaar zitten). Laten we het koolstofatoom waaraan de OH vastzit de wortel van die boom noemen.

Tijd voor wat recursiewerkzaamheden:
Als je het wortel C-atoom weglaat uit de boom dan valt hij uiteen in een aantal sub-bomen.
Oké, laten we een ingewikkelde boom nemen (ik heb werkelijk geen enkel geen idee hoe deze alcohol heet en hoe 'íe smaakt; ik verzin dit ter plekke):

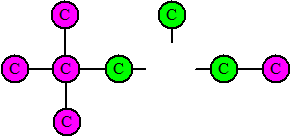
De wortel is die groene C en die laten we weg waardoor de boom in drie stukken uit elkaar valt. We beschouwen de C die oorspronkelijk aan de weggelaten C vastzat als de nieuwe wortel van elk van die sub-bomen.

Vraag jezelf af: "zou ik van dit laatste plaatje de oorspronkelijke boom kunnen terugfabriceren?"
Natuurlijk! Je zet al die drie groene C's gewoon vast aan een nieuwe C en plakt daar weer een OH aan. Gewoon het "filmpje terugdraaien", of de "schade herstellen"" als je dat beter vindt klinken. De volgorde waarin je die drie aan elkaar plakt doet er niet toe; ze zitten aan dezelfde C en het zijn er maar drie, dus dat levert dezelfde boom op.

Het zou natuurlijk ook kunnen dat er geen drie maar minder sub-bomen ontstaan (als de OH aan de rand zit). In zo'n geval doen we gewoon alsof er toch drie bomen te zijn door fictieve "lege" bomen toe te voegen. Zó bijvoorbeeld:

Als je die drie "sub-bomen" weer samenvoegt krijg je weer gewoon de oorspronkelijke boom. Er zouden zelfs 2 lege bomen kunnen zijn. Hoe dan ook; het komt er op deze manier elke keer op neer dat we drie sub-bomen samenvoegen om een nieuwe boom te krijgen.
Beschouw die drie sub-bomen als de "dingen" die om de hoekpunten van een driehoek worden gelegd. Net als de samengelijmde knikkers hierboven.

Een willekeurige boom kunnen we dus krijgen door drie bomen aan elkaar te zetten. Dat kunnen op zich weer bomen met 0, 1, 2, 3, 4... C-atomen zijn. En van al die bomen zijn er weer een aantal varianten mogelijk. Stel dat er van een boom met k C-atomen in totaal R_k varianten mogelijk zijn (dus zoals we bij de alcoholen al zagen: R₀ = 1, R₁ = 1, R₂ = 1, R₃ = 2, R₄ = 4, ....en de rest weten we nog niet)
Om dan het totaal aantal mogelijkheden op te schrijven moeten we de cykelindex van S₃ gebruiken, maar met
f = R₀x⁰ + R₁x¹ + R₂x²+^.... • De term met xⁿ staat voor het aantal sub-bomen met n C-atomen (de aan elkaar gelijmde knikkers van verdieping 1 hierboven)
• De factoren R_n staan voor het aantal varianten van een sub-boom van n C-atomen (de verschillende soorten knikkers van verdieping 2 hierboven)

De cykelindex wordt dan:

Als je voor de f 's dat polynoom invult, en dan alle haakjes zou wegwerken (stel dat je dat zou kunnen) dan zou je een machtsreeks in x krijgen. De macht n van xⁿ daarin stelt het totaal aantal C-atomen in de drie sub-bomen samen voor, en de coëfficiënt ervan geeft het aantal manieren waarop het kan. De uiteindelijke boom die de drie sub-bomen samen gaan vormen heeft dus n + 1 C-atomen, immers je voegt bij het samendoen er één toe (plus een OH).
Dus als je de formule met x vermenigvuldigt, dan komt de coëfficiënt van xⁿ precies overeen met het aantal mogelijkheden voor een boom met n C-atomen. Als je er dan ook nog 1 bij optelt om rekening te houden met de lege boom, dan moet je als antwoord precies f(x) krijgen!!!

Het is gelukt!!!
We hebben een vergelijking voor de functie f.
Nou ja.... een soort van vergelijking. 't Is niet een gewone vergelijking f(x) = .... met x-en erachter. Dit hier is meer een soort recept waar f aan voldoet. Dat noemen we een functionaalvergelijking.
Nu nog even gewoon deze functionaalvergelijking omzetten in een "gewone" vergelijking.

Helaas is dat tot nu toe nog niemand gelukt!

Het beste wat we kunnen doen is een reeksontwikkeling voor dat monster aan de linkerkant maken.
Stel f(x) = R₀ + R₁x + R₂x² + R₃x³ + R₄x⁴ + R₅x⁵ + .....
Wacht even; we weten R₀, R₁, R₂, R₃ en R₄ al: f(x) = 1 + x + x² + 2x³ + 4x⁴ + R₅x⁵ + R₆x⁶ + .....
Vul dit in in die functionaalvergelijking, werk alle haakjes weg en nemen gelijke machten van x samen.

Ik zal een beginnetje maken. Laat ik maar eens op zoek gaan naar R₅, dus de coëfficiënt van x⁵ Dat moet dan daar in die teller de coëfficiënt van x⁴ zijn, want er staat ook nog een x voor.
Op jacht naar machten x⁴ dus:

(de blauwe getallen hieronder zijn binomiaalcoëfficiënten)
f(x)³ krijgt als machten van x⁴uiteindelijk 3 • 1 • 1 • 4x⁴ + 3 • x • x • x² + 3 • 1 • x² • x² + 6 • 1 • x • 2x³ = 30x⁴
3f(x)f(x²) krijgt als machten van x⁴ uiteindelijk 3 • 1 • (x²)² + 3 • x² • (x²)¹ + 3 • 4x⁴ • 1² = 18x⁴
2f(x³) heeft geen machten van x⁴
De uiteindelijke teller wordt dus 48x⁴
Delen door 6 en vermenigvuldigen met x geeft een term 8x⁵ dus R₅ = 8

Dan is de tussenstand f(x) = 1 + x + x² + 2x³ + 4x⁴ + 8x⁵ + R₆x⁶ + ..... en kunnen we op zoek naar R₆
Typisch een werkje voor een computer-algebraprogramma.
Hier zijn wat resultaten:

R₁	R₂	R₃	R₄	R₅	R₆	R₇	R₈	R₉	R₁₀	R₁₁	R₁₂	R₁₃	R₁₄
1	1	2	4	8	17	39	89	211	507	1238	3057	7639	19241