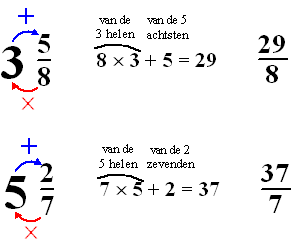|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Breuken veranderen. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Een breuk dat is natuurlijk
eigenlijk gewoon twee getallen gedeeld door elkaar. Bij de breuk 4/6 staat daar eigenlijk gewoon "4 gedeeld door 6" Het gedeelte boven de deelstreep heet de TELLER en een gedeelte onder de deelstreep heet de NOEMER. In het voorbeeld is de teller gelijk aan 4 en de noemer gelijk aan 6. En nou komt het: |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Als ik bijvoorbeeld van
4/6 de
teller en de noemer vermenigvuldig met 8, dan krijg ik
32/48
en dat is dezelfde breuk als 4/6 En als ik allebei door 2 deel krijg ik 2/3 en ook dat is dezelfde breuk als 4/6. Wat hebben we hieraan? Waarom zou je dat willen? Nou, er zijn twee gevallen waarin dat wel een handige eigenschap van breuken is....... |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1. Breuken vereenvoudigen. Kijk, als je die teller en die noemer door het zelfde getal kunt DELEN, dan worden ze allebei kleiner en dus wordt de hele breuk wat eenvoudiger. Kleinere getallen zijn nou eenmaal eenvoudiger dan grote getallen. Zo kun je van de breuk 36/48 de teller én de noemer door 3 delen, en dan krijg je 12/16 en dat is al een stuk eenvoudiger. Maar wacht eens even... van
12/16
kun je de teller en de noemer weer beiden door 4 delen. Dat geeft
3/4,
en dat is nóg eenvoudiger. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2. Breuken gelijknamig maken. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Het woord zegt het al: als
breuken gelijknamig zijn, dan is hoe je ze noemt
hetzelfde, dus zijn de noemers gelijk! Breuken heten dus gelijknamig als hun noemers (dat deel onder de streep) gelijk zijn. En dat is vaak handig om ze bijvoorbeeld met elkaar te vergelijken (of zelfs ook om ze bij elkaar op te tellen maar dat komt in een volgende les nog wel). Als je twee breuken verandert door hun tellers en noemers met hetzelfde getal te vermenigvuldigen, dan kun je ervoor zorgen dat die noemers gelijk worden. Neem bijvoorbeeld de breuken 5/7 en 3/5 Als je van die eerste breuk teller en noemer met 5 vermenigvuldigt krijg je 25/35 As je van die tweede breuk teller en noemer met 7 vermenigvuldigt dan krijg je 21/35 Zo zie je makkelijker dat die eerste breuk groter is dan die tweede, immers het gaat in beide gevallen om 35-sten. Maar die eerste breuk heeft er 25 van, en die tweede maar 21..... Neem bijvoorbeeld de breuken 7/8 en 5/6 Als je van die eerste breuk teller en noemer met 6 vermenigvuldigt krijg je 42/48 Als je van die tweede breuk teller en noemer met 8 vermenigvuldigt dan krijg je 40/48 Ik hoop dat je ziet dat je deze twee breuken nog weer kunt vereenvoudigen.... Van beiden kun je teller en noemer nog door 2 delen, en dat geeft 21/24 en 20/24 . Zo blijven de noemers gelijk....... Dat had je ook direct kunnen bereiken als je had gezien dat van de eerste oorspronkelijke breuk de noemer en de teller met 3 kunt vermenigvuldigen (3 ´ 8 = 24), en dat geeft hetzelfde als van die tweede breuk de noemer en de teller met 4 (4 ´ 6 = 24). Dan had je meteen 21/24 en 20/24 gevonden. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Helen eruit halen. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Van hele getallen kun je ook best
breuken maken als je dat wilt. Kijk maar: 5 kun je schrijven als 5/1 en 8 als 8/1 en 134 als 134/1 enzovoort. 't Is een beetje flauw natuurlijk, maar geef toe: het zijn wél breuken geworden. En die breuken kun je op de manier als hierboven weer veranderen. Door teller en noemer met hetzelfde getal te vermenigvuldigen. Zo is 5 = 5/1 = 10/2 = 15/3 = .....= 90/18 = ... = 1605/321 = ... maar eh... het nut? Het nut van al dit "gedoe" komt als je een breuk krijgt die bestaat uit een geheel getal plus een breukdeel erachter. Neem bijvoorbeeld 35/8 dat is het hele getal 3 plus de breuk 5/8. Als je nou van die 3 óók "achtsten" maakt, dan kun je het hele getal en het breukdeel samen als één gewone breuk schrijven en dat kan erg handig zijn als je moet optellen of vermenigvuldigen met breuken. 3 = 24/8 Dus 35/8 = ( 24/8 plus 5/8) en dat is 29/8 En op dezelfde manier is 52/7 = ( 35/7 plus 2/7 ) = 37/7 zie je al hoe het snel kan? |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Helen er weer inzetten. Andersom kan natuurlijk ook. Als je een breuk hebt waarvan de teller groter is dan de noemer, dan kun je er weer helen inzetten. Vooral handig om ongeveer in te schatten hoe groot die breuk is. Neem bijvoorbeeld 324/7 . Daar zet je helen in door steeds de volgende drie vragen te stellen en te beantwoorden: |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Daarom is 324/7 = 462/7 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
© h.hofstede (h.hofstede@hogeland.nl) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||