| |
© h.hofstede (h.hofstede@hogeland.nl)
|
|
|
Bomen. |
| |
|
|
|
|
 |
| |
|
|
|
Laten we beginnen met
maar weer wat termen.
• Een acyclische graaf
is een graaf die geen cykels bevat. Zo'n graaf heet ook wel een
bos.
• Een boom is een
samenhangende acyclische graaf. (leuk hé? een bos
bestaat uit bomen!) |
| |
|
|
|
| Hier zie je een paar
bomen (en met z'n vijven vormen ze uiteraard ook weer een bos!): |
| |
|
|
|
|
 |
| |
|
|
|
| Een boom heeft de
volgende prettige eigenschap: |
| |
|
|
|
| elk willekeurig paar knooppunten is
door precies één route met elkaar verbonden. |
|
| |
|
|
|
| Bewijs uit het
ongerijmde: |
|
 |
| |
|
|
|
Stel dat er twee verschillende routes R1 en R2
zijn die de knooppunten A en B met elkaar verbinden.
Omdat R1 en R2 ongelijk zijn bestaat er een
verbindingslijn V die wel in R1 zit, maar niet in R2.
Stel dat die V de knooppunten X en Y met elkaar verbindt.
Bekijk nu de graaf die bestaat uit alle knooppunten en verbindingslijnen
van R1 en R2 samen, maar laat daar verbindingslijn
V uit weg.
De overblijvende graaf is dan samenhangend, immers de ene kant van de
breuk XY is met A verbonden en de andere kant met B.
Dus bevat de overblijvende graaf een route van Y naar X.
Maar dan bevat de hele graaf (als je V weer toevoegt) een cykel
(namelijk die route plus V)
Dat is tegenstrijdig met het feit dat de graaf acyclisch is! |
|
■ |
|
|
|
| |
|
|
|
| Hier zijn nog een
paar eigenschappen van bomen. Waarschijnlijk zul je ze wel logisch
vinden en heb je de bewijsjes ernaast helemaal niet nodig. |
| |
|
|
|
| • |
Als er in een graaf zonder cykels
voor elk willekeurig paar knooppunten precies één
route is die ze verbindt, dan is die graaf een boom.
(de omgekeerde stelling van de bovenstaande). |
 |
| • |
Voor een boom geldt: V
= K - 1 |
 |
| • |
In een boom is elke verbindingslijn
een lijnsnede |
 |
| • |
Een boom heeft minstens twee
knooppunten met graad 1.
Als er precies twee zijn is de graaf een route. |
 |
|
|
| |
|
|
|
| |
|
|
|
|
Opspannende bomen.
(eng: "spanning trees") |
| |
|
|
|
Een
deelgraaf van een graaf G is een graaf die
bestaat uit een deel van de knooppunten en verbindingslijnen van G.
Een opspannende deelgraaf van
een graaf G is een deelgraaf die wel alle knooppunten bevat. Je
kunt dus een deelgraaf van G maken door eventueel een aantal
verbindingslijnen weg te laten.
Laten we een opspannende boom
van G bekijken (dat is een opspannende deelgraaf die een boom is)
Zo'n boom kun je zien als het minimale deel van G dat alle
knooppunten met elkaar verbindt, met geen enkele "overbodige"
verbindingslijn meer.
Je kunt je misschien voorstellen dat het best nuttig kan zijn zo'n
opspannende boom te maken.
Stel bijvoorbeeld dat je de steden A, B, C, D, E, F, G hieronder door een
spoorwegstelsel met elkaar moet verbinden (in plaats van
spoorwegstelsel kun je ook lezen "kabelnetwerk" of
""elektriciteitaansluitingen"). Om de kosten zo laag
mogelijk te houden wil je dan natuurlijk zo min mogelijk
verbindingslijnen nodig hebben, maar de graaf moet wel samenhangend
zijn. Een opspannende boom dus!!
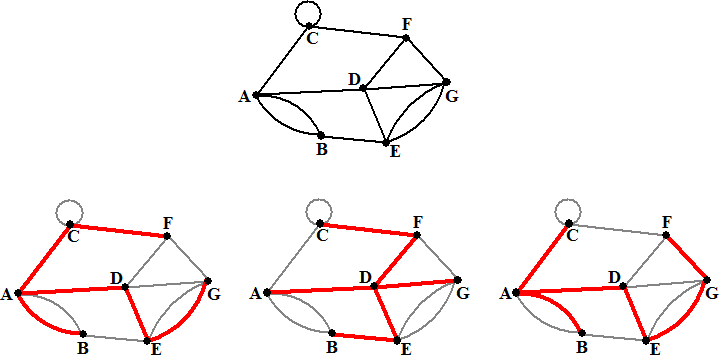
Daar zijn meerdere mogelijkheden voor. Hieronder zie je drie
roodgekleurde opspannende bomen van dezelfde graaf. |
| |
|
|
|
|
 |
| |
|
|
|
| Elk van die opspannende bomen
heeft 6 verbindingswegen, maar dat wist je natuurlijk al: er zijn
7 knooppunten en voor een boom geldt V = K - 1 |
| |
|
|
|
Goh; hoeveel opspannende bomen hééft
een graaf eigenlijk?
- formule van Cayley- |
| |
|
|
|
Om dat aantal te bepalen gaan we
verbindingslijnen "samentrekken".
Een verbindingslijn trek je samen door hem weg te laten en van de beide
eindpunten één nieuw knooppunt te maken.
In de figuur hiernaast is de blauwe verbindingslijn BD samengetrokken
Als we uit graaf G de verbindingslijn v samentrekken, dan noemen
we de nieuwe graaf G\v.
Denk erom dat dat wat anders is dan de graaf G - v want dat
is de graaf die je krijgt als je v gewoon weglaat zonder
iets samen te trekken!
Twee beweringen: |
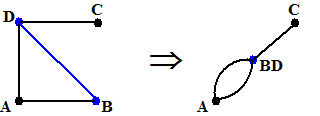 |
| |
|
|
|
| 1. |
aantal opspannende bomen van G -
v = aantal opspannende bomen van G die v niet
bevatten (lijkt me logisch) |
| 2. |
aantal opspannende bomen van G\v
= aantal opspannende bomen van G die v wél bevatten. Die bomen
lopen immers via het samengetrokken knooppunt, dus gebruiken de
verbindingslijn v van de oorspronkelijke graaf. |
Als je beide beweringen hierboven bij elkaar optelt krijg je:
(aantal opspannende bomen van G) = (aantal opspannende bomen van G -
v) + (aantal opspannende bomen van G\v)
In formulevorm (A = aantal opspannende bomen):
A(G) = A(G - v) + A(G\v)
Dat is een manier om via recursie het aantal opspannende bomen van een
graaf te tellen.
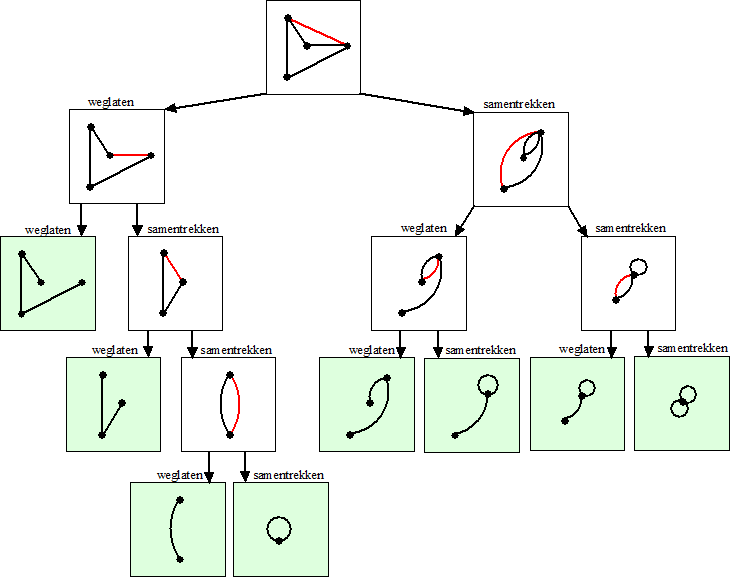
Kijk maar naar het volgende stripverhaal (de verbindingslijn die
wordt weggelaten/samengetrokken is steeds rood gekleurd)
De groene vlakjes zijn "klaar": dat zijn bomen. |
| |
|
|
|
|
 |
| |
|
|
|
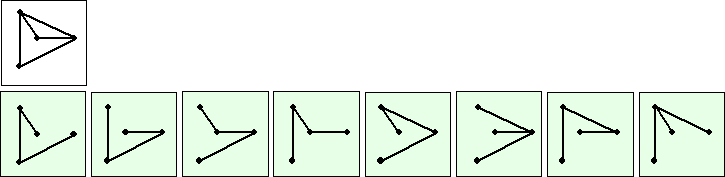
| Daaraan zie je dat de graaf
bovenaan 8 opspannende bomen heeft. Hieronder zijn ze nog eens in de
graaf zelf getekend als je de samengetrokken delen weer "uitschuift" (de groene figuurtjes hierboven van links naar
rechts). |
| |
|
|
|
|
 |
| |
|
|
|
Een volledige graaf opspannen.
Voor een volledige graaf met
n knooppunten (Kn, weet je nog?) kun je vrij
eenvoudig het aantal opspannende bomen tellen.
Dat kun je doen door een opspannende boom als een rij getallen weer te
geven. Het werkt zó:
• Nummer eerst de knooppunten van Kn van 1 tm
n
• Noem nu K1 het nummer van eerste knooppunt van graad 1 in
de opspannende boom B.
• Het knooppunt dat aan K1 grenst (dat is er dus maar één)
noemen we B1.
• Laat nu K1 weg en ga op zoek naar het eerstvolgende
knooppunt met graad 1 in de boom. Dat noemen we K2.
• Het knooppunt dat aan K2 grenst heet B2.
Zo gaan we alsmaar door tot er nog maar twee knooppunten over zijn
Dat geeft een rij getallen B1, B2, ..., Bn
- 2 die de opspannende boom vastleggen.
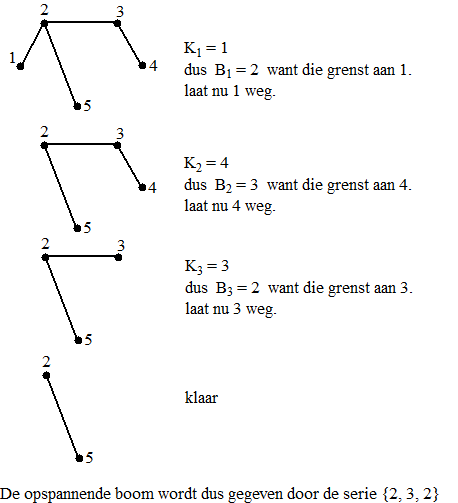
Hier zie je het systeem in werking, bij een opspannende boom van K5
: |
| |
|
|
|
|
 |
| |
|
|
|
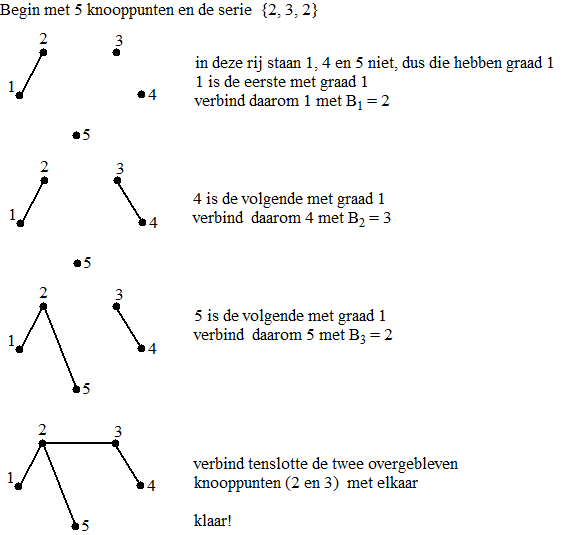
| Andersom kun je van elke serie
{ , , } van drie B-getallen een opspannende boom
van K5 tekenen. Kijk maar hoe het in omgekeerde volgorde
gaat: |
| |
|
|
|
|
 |
| |
|
|
|
Ga zelf maar na dat dit altijd
lukt!
Er is dus een 1-op-1 relatie tussen de opspannende bomen van Kn
en een rijtje van n-2 getallen (allemaal van 1 tm n)
Dus er zijn evenveel rijtjes als opspannende bomen. En dat zijn er
nn - 2 |
| |
|
|
|
|
Een volledige graaf Kn
heeft nn - 2 opspannende bomen. |
|
| |
|
|
|
Merk nog even op dat we op deze
manier alle opspannende bomen krijgen, ook bomen die isomorf met elkaar
zijn.
Zo heeft K6 dus 64 = 1296 opspannende bomen,
maar er zijn slechts zes niet-isomorfe opspannende bomen! |
| |
|
|
|
| |
|
|
|
|
OPGAVEN |
| |
|
|
|
| 1. |
Hoeveel bomen met 6 knooppunten
bestaan er? |
| |
|
| 2. |
Een verzadigd koolwaterstof
molecuul is een CmHn
molecuul waarin elk C-atoom aan vier andere atomen is
gebonden, en elk waterstof atoom aan één ander atoom
Toon aan dat dan geldt n = 2m + 2 |
| |
|
|
|
| 3. |
Teken de volgende opspannende
bomen: |
| |
|
|
|
| |
a. |
{4, 1, 1, 2, 3}
van K7 |
| |
|
|
|
| |
b. |
{2, 6, 4, 3, 3, 2, 5}
van K9 |
| |
|
|
|
| 4. |
Neem een
cykel en voeg daar één nieuw knooppunt aan toe.
Verbind dit knooppunt met alle al bestaande knooppunten van de
cykel.
Dan krijg je een wiel.
De nieuwe verbindingslijnen heten de spaken van
het wiel.
Geef een formule voor het aantal opspannende bomen van een wiel
met n spaken. |
| |
|
|
|
| |
|
|
 |
|
|
© h.hofstede (h.hofstede@hogeland.nl)
|