snijden met kegels en bollen

© h.hofstede (h.hofstede@hogeland.nl)

Snijden met Bollen en Kegels

We hebben intussen al snijlijnen van vlakken en snijpunten van lijnen en vlakken bekeken en berekend. Maar ook gekromde vlakken kunnen natuurlijk doorsneden worden.
Daarover gaat deze les.

Een bol met een vlak snijden.

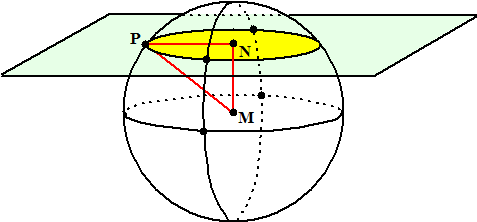
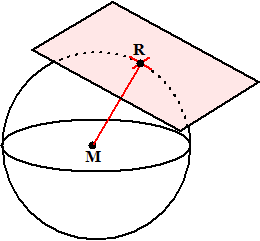
Als je een bol snijdt met een (plat) vlak, dan is de doorsnede natuurlijk een cirkel. De vraag alleen is: hoe groot is die cirkel en waar ligt het middelpunt?

Hiernaast zie je wat er aan de hand is. Natuurlijk hoeft het vlak niet zo mooi horizontaal te zijn, maar kan het ook scheef liggen, voor de figuur maakt dat niet uit.

Het middelpunt N van de snijcirkel kun je vinden als je je realiseert dat MN loodrecht op het vlak V staat. Teken dus een lijn door M loodrecht op V en snij die met V. Dat geeft N.

De straal R van de snijcirkel is daarna een makkie: kijk maar naar driehoek MNR.
MN is nu bekend, MP was al bekend (straal van de bol) dus met Pythagoras is eenvoudig de straal NP van de snijcirkel te berekenen.

Die eerste stap (die loodrechte lijn MN) kun je uitvoeren door "meetkundig te redeneren" zoals in deze les is omschreven. Je kunt ook een "berekening met vectoren" maken zoals in deze les is omschreven.
Ik zal één voorbeeld op beide manieren uitvoeren.

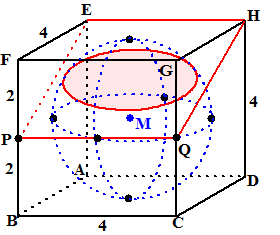
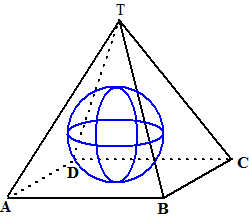
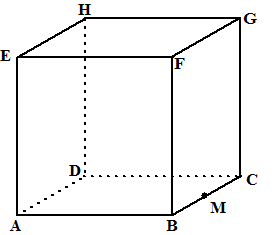
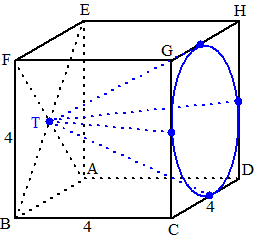
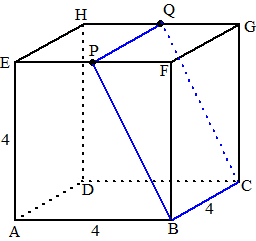
In een kubus ABCD.EFGH met ribben 4 is de ingeschreven bol getekend. Het vlak EHPQ (waarbij P en Q de middens van BF en CG zijn) snijdt de bol volgens een snijcirkel.

Bereken de straal van die snijcirkel.

Met vectormeetkunde.
Kies als oorsprong punt A, en noem het middelpunt van de snijcirkel N

Een vergelijking van EPQH is dan x + 2z = 8

Invullen in de vergelijking: 2 + λ + 2(2 + 2λ) = 8 geeft λ = ²/₅
De lengte van MN is dan ²/₅ van de lengte van de richtingsvector
MN is dan dus gelijk aan ²/₅ • √(1² + 0² + 2²) = ²/₅√5

Met meetkundig redeneren.

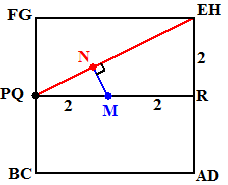
In het zijaanzicht hiernaast staat MN loodrecht op EP (immers dan staat MN loodrecht op EP en op EH, dus op het hele vlak EHPQ
Daarom is driehoek MNQ gelijkvormig met driehoek ERQ
EQ = √(4² + 2²) = √20 = 2√5
Dan is ^MN/_MQ = ^ER/_EQ dus ^MN/₂ = ²/_2√5

Dat geeft MN = ⁴/_2√5 = ²/₅√5

Hetzelfde resultaat als bij de vectormeetkunde-aanpak.

De bol heeft straal R = 2, dus daarna geldt voor de straal r van de snijcirkel
r² + (²/₅√5)² = 2² dus r² = 3,2 en r = √3,2 = ⁴/₅√5

Een lijn met een kegelmantel snijden.

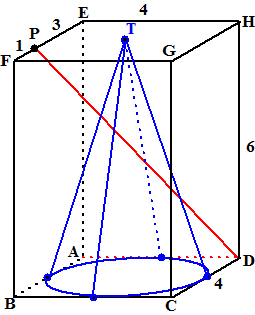
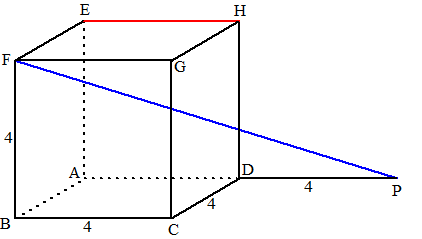
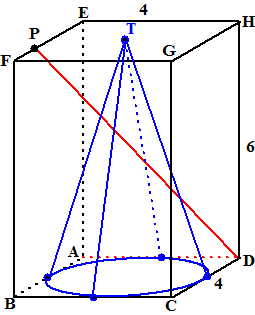
In de balk hiernaast zie je een kegel, die gesneden wordt door de lijn PD waarbij P op EF ligt zodat PE = 3.
De lijn snijdt de kegelmantel in twee punten V en W.

Als je die wilt tekenen is er eigenlijk maar één methode:

leg een vlak door de lijn en de top
snij dat vlak met de grondcirkel.

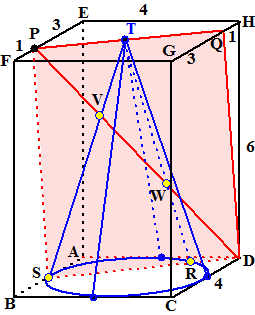
In dit geval zou dat vlak PTD worden en dat is hetzelfde als PQDS in de figuur hiernaast.

Dat vlak snijdt de grondcirkel in de punten R en S.

Trek de lijnen ST (staat er al) en RT.

Die liggen zowel op de kegelmantel als in vlak PQDS dus die kun je snijden met de lijn PD.

Dat geeft de snijpunten V en W.

(bonusvraagje voor echte doorzetters: "Bereken VW in twee decimalen nauwkeurig" ; de oplossing staat hier).

Het middelpunt van een bol construeren.

Om het middelpunt van een bol te vinden hangt het er nogal van af wat er precies bekend is van die bol. Twee belangrijke principes kun je bij je jacht op het middelpunt gebruiken.

principe 1.
Als een vlak een bol raakt, dan ligt het middelpunt van die bol op de lijn die door het raakpunt gaat en loodrecht op dat vlak staat.

Zie de figuur hiernaast.

Voorbeeld van principe 1 in werking.

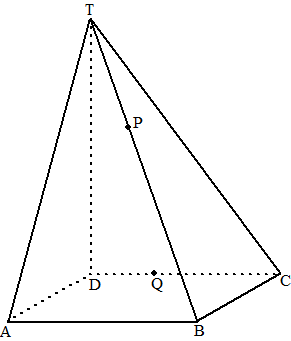
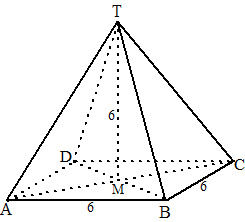
Hiernaast zie je een regelmatige piramide T.ABCD met als grondvlak een vierkant met zijden 4 en met hoogte 6.
Bereken de straal van de ingeschreven bol (dat is de bol die alle vlakken van de piramide raakt).

Vanwege de symmetrie van de figuur zal de bol het grondvlak in het midden raken.
Omdat de bol het grondvlak raakt zal het middelpunt liggen op een lijn vanaf het midden van het grondvlak recht omhoog naar de top T

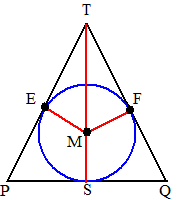
Bekijk nu de verticale doorsnede PQT hiernaast (P en Q zijn de middens van AD en BC)
Ergens op TS ligt punt M, maar we weten dat de lijnen ME en MF naar de raakpunten loodrecht op de zijden moeten staan.
Omdat MF = MS = r (Straal van de bol) zijn de driehoeken MSQ en MFQ congruent (rechte hoek plus twee zijden gelijk)
Dus is FQ = SQ = 2
TM = 4 - MS = 4 - r
TF = TQ - 2 = √20 - 2
Pythagoras in TFM: r² + (√20 - 2)² = (4 - r)²
r² + 20 - 4√20 + 4 = 16 - 8r + r²
8r = 4√20 - 8
r = 0,5√20 - 1 (= 1,236...)

principe 2.
Als je twee punten van de bol hebt, dan ligt het middelpunt van de bol in het middelloodvlak van die twee punten. Dat is logisch, immers het middelpunt heeft gelijke afstanden tot die twee punten (namelijk de straal van de bol).

Een middelloodvlak is nou eenmaal de verzameling van alle punten die gelijke afstanden tot de gegeven punten hebben, dus ook het middelpunt van de bol zit daarbij.

Voorbeeld van principe 2 in werking.

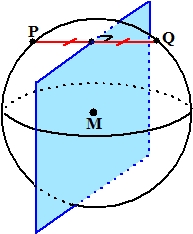
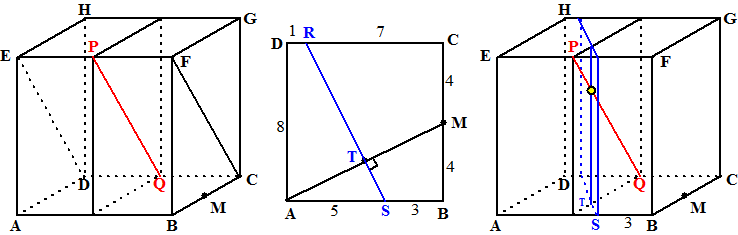
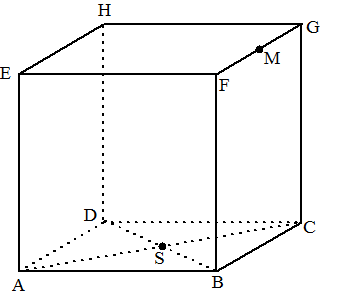
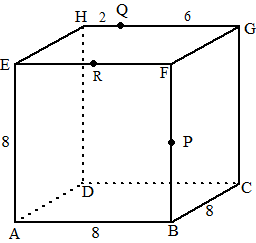
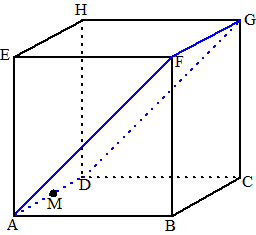
In een kubus ABCD.EFGH met ribben 8 is M het midden van BC.
Een bol gaat door de punten A, H, G en M.
Construeer het middelpunt van deze bol.

We hebben hier 4 punten van de bol gegeven, dus het middelpunt ligt in alle middelloodvlakken van koppels van die punten.

We beginnen met de makkelijkste middelloodvlakken.
Het middelloodvlak van AH is vlak EDCF en het middelloodvlak van HG is het verticale vlak dat de kubus doormidden snijdt. Zie de figuur linksonder.

We weten nu dus al dat het middelpunt van de bol ergens op de snijlijn PQ van die twee middelloodvlakken ligt.

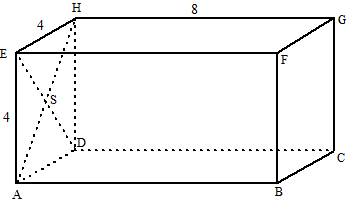
Over naar het middelloodvlak van A en M. Dat staat loodrecht op het grondvlak. Teken daarom in het grondvlak een lijn door het midden van AM loodrecht op AM. Zie de middelste figuur; dat geeft SR met de afmetingen zoals aangegeven (reken zelf maar na)
Teken tenslotte in de kubus de snijlijn van dit middelloodvlak met lijn PQ. Dat geeft het gele punt in de rechterfiguur en dat is het middelpunt van de gezochte bol.

Twee bollen met elkaar snijden.

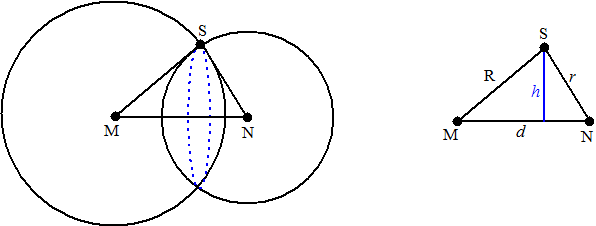
Als je twee bollen met elkaar snijdt krijg je een snijcirkel.
De straal daarvan kun je het best berekenen door de middelpunten van de bollen met elkaar te verbinden, en dan het vlak dat loodrecht op die verbindingslijn staat en waar de snijcirkel in ligt te bekijken.

Je krijgt dan een driehoek MNS met als zijden de straal R van de ene bol, de straal r van de andere bol en de afstand d tussen de middelpunten van beide bollen.
De straal van de snijcirkel is dan de hoogte h van deze driehoek.
Dat moet lukken.....cosinusregel bijvoorbeeld......

Toch maar een voorbeeldje

Twee bollen met stralen 4 en 6 hebben afstand tussen hun middelpunten 8. Bereken de straal van de snijcirkel.

R = 6 en r = 4 en d = 8 geeft in de driehoek 4² = 6² + 8² - 2 • 6 • 8 • cos(∠SMN)
-84 = -96cos(∠SMN)
cos(∠SMN) = ⁷/₈
Dan is sin(∠SMN) = √(1 - cos²(∠SMN)) = √(1 - ⁴⁹/₆₄) = ¹/₈√15
sin(∠SMN) = ^h/₈ dus h = 8 • ¹/₈√15 = √15 en dat is de straal van de snijcirkel.

OPGAVEN

Van de piramide T.ABCD hiernaast is het grondvlak een vierkant met zijden 6. D is de loodrechte projectie van T op het grondvlak en DT = 8
Op DT ligt een punt P zodat BP = 2 • PT
Op CD ligt een punt Q zodat DQ = 2
V is het vlak door P en Q dat evenwijdig is aan DT.

Vlak V snijdt TC in R en AB in S

Teken de doorsnede van V met de piramide.

Bereken de inhoud van lichaam PRQS.BC

277¹/₃

Bol b heeft D als middelpunt en straal 5.
Bereken de straal van de snijcirkel van b en vlak BCT.

1,4

ABCD.EFGH is een kubus met ribben 4.
P is een punt op het verlengde van AD zodat AP = 8.
Een cilinder heeft als as EH en straal √7.

Onderzoek of deze cilinder de lijn FP snijdt.

ABCD.EFGH is een kubus met ribben 4.
T is het snijpunt van AF en EB.
K is een kegel met top en grondvlak de ingeschreven cirkel van vlak DCGH.

Construeer het snijpunt van de kegelmantel met CE.

Q is het midden van GC, R het midden van DH
Bereken in twee decimalen nauwkeurig de kortste afstand van Q naar R over de kegelmantel.

5,78

In kubus ABCD.EFGH met ribben 8 is M het midden van FG, en S het snijpunt van AC en DB.
Een bol raakt het grondvlak ABCD in S en raakt ribbe FG in M.
Construeer in de figuur hieronder het middelpunt van die bol en bereken de straal.

Een regelmatige vierzijdige piramide heeft zijden van het grondvlak 6 en hoogte ook 6. M is het middelpunt van het grondvlak.

Een bol met middelpunt M gaat door A, B, C en D
Bereken de straal van de snijcirkel van deze bol met vlak TBC.

√6

ABCD.EFGH is een kubus met ribben 6.
Bereken de straal van de bol die raakt aan vlak EFGH en die verder door de punten A, B en C gaat.

4,5

In kubus ABCD.EFGH is P het midden van EF en Q het midden van HG.
Bereken de straal van de snijcirkel van de ingeschreven bol van de kubus met vlak BPQC. Geef je antwoord in twee decimalen nauwkeurig.

(de ingeschreven bol is de bol die alle zijvlakken raakt)

3,35

In kubus ABCD.EFGH met ribben 8 is P het midden van BF, R het midden van EGF en Q een punt van HG zodat HQ = 2.

Een bol gaat door E, A, D en P. Construeer het middelpunt van deze bol en bereken de straal.

√17

Q wordt gedraaid om as DF. Daarbij beschrijft Q een cirkel. Teken het vlak waar deze cirkel in ligt en construeer het middelpunt van deze cirkel.

Gegeven is een balk ABCD.EFGH met AB = 8 en AD = AE = 4 (zie onderstaande figuur).
S is het snijpunt van AH en CD
Een bol gaat door A, S en C.
Construeer lijn l waarop het middelpunt van deze bol ligt.

10.

Gegeven is kubus ABCD.EFGH met ribben 4.
M is het midden van AB.
b is de bol met middelpunt M en straal 3.
Bereken de oppervlakte van het deel van vlak DAFG dat zich binnen b bevindt.

11.

ABCD.EFGH is een balk met afmetingen zoals hiernaast.
In deze balk is een kegel getekend met de top in het midden van vlak EFGH en als grondcirkel de ingeschreven cirkel van vlak ABCD.

P is een punt ergens op EF.

Waar moet punt P gekozen worden zodat de lijn PD de kegelmantel raakt?