| De constructie van x2
en Öx. |
|
|
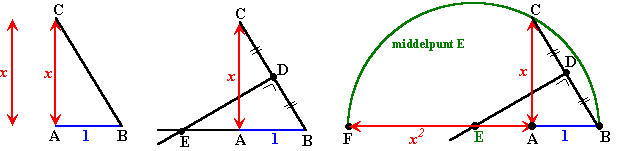
| 1. x2 |
|
|
|
 |
|
|
Het bewijs:
Omdat de driehoeken ABC en DBE gelijkvormig zijn geldt EB :
BD = BC : AB ofwel EB•AB = BD•BC
Maar AB = 1 en BD = ½BC dus dat wordt EB
= ½BC2
Uit driehoek ABD zien we dat 12 + x2 =
BC2 dus de vergelijking wordt EB = ½(1 + x2)
FA = EF + EA = EB + EA = (EA + 1) + EA = 2•EA + 1 = 2•(EB - 1) + 1
= 2•EB - 1
Substitueer de uitdrukking voor EB: FA = 2•(½(1 + x2))
- 1 = 1 + x2 - 1 = x2 |
|
|
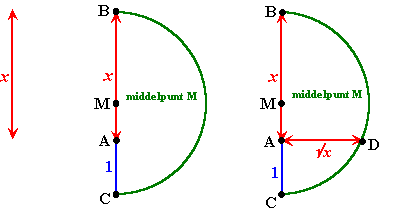
| 2. Öx |
|
|
|
Daarmee kun je het probleem:
"gegeven een rechthoek, construeer
een vierkant met dezelfde oppervlakte"
oplossen. |
|
|
 |
|
|
Het bewijs
In driehoek AMD geldt: AD2 = MD2 -
AM2
MD = ½•BC = ½(x + 1) = ½x + ½
AM = MC - 1 = MD - 1 = ½(x + 1) - 1 = ½x - ½
Substitueren geeft AD2 = (¼x2 + ½x +
¼) - (¼x2 - ½x + ¼) = x
Dus AD = Öx
Eigenlijk is het een
variant van de oude stelling:
| "In
een rechthoekige driehoek is de lengte van de hoogtelijn
vanuit de rechte hoek het meetkundige gemiddelde van de
twee stukken waarin hij de overstaande zijde
verdeelt" |
|
|
|
| |
|