Constructies met Lucifers.
Het klinkt misschien niet zo serieus, maar waarom niet met lucifers?  Passer en liniaal zijn toch ook maar zomaar verzonnen apparaten.
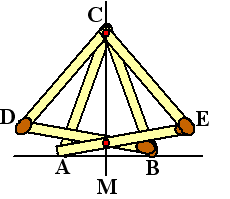
T.R. Dawson ontdekte zelfs dat ELK punt dat je met passer en liniaal kunt construeren óók met lucifers is te construeren!!!! Kortom, 't is gewoon net zo interessant als het klassieke construeren. Hiernaast zie je bijvoorbeeld een 7-luciferconstructie om het midden van een gegeven lijnstuk AB te construeren.
De zevende lucifer is CM en die deelt lijnstuk AB doormidden.
Je kunt er trouwens ook hoek DCE en hoek ACB mee doormidden delen.

Voor de volgende teken ik niet meer allemaal lucifers (wordt wat onoverzichtelijk) maar vervang ik "lucifer" door "lijnstuk van constante lengte".

Rechts in de onderste figuur staat de constructie van een vierkant.

Leg gelijkzijdige (uiteraard) driehoeken ABC, BCD en BDE.
Kies AF willekeurig in driehoek ABC.
G kun je maken door lucifers vanaf F en B tegen elkaar te laten vallen.
Maak driehoek GHB.
I is het snijpunt van ED en HG.
BJ (door F) en de lucifer door BI zijn 2 zijden van het vierkant.
K weer door lucifers vanaf de twee uiteinden van het vierkant tegen elkaar te laten vallen.